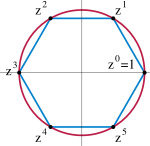
Speciális unitér csoport
A speciális unitér csoport, jelölés szerint a matematikában az olyan unitér mátrixok csoportja, melyek determinánsa egy. A csoport asszociatív csoportművelete a mátrixszorzás, és mivel a speciális unitér csoport egy sima sokaság, amelyben a mátrixszorzás tetszőlegesen sokszor differenciálható, ezért egy Lie-csoport.
Az unitér mátrixok determinánsának abszolút értéke egy, ezt a tulajdonságot szűkíti tovább a speciális unitér csoport. Továbbá, a speciális unitér csoport normálosztója az unitér csoportnak (), mely az unitér mátrixok csoportja, mely részcsoportja az általános lineáris csoportnak. Formálisabb jelölés szerint .
Az csoportok legegyszerűbb esete az , mely egy triviális csoport, tehát egyetlen eleme van, az egységelem, ami ebben az esetben . Az izomorf azon kvaterniók csoportjához, melyeknek normája egy, ezáltal diffeomorf a 3-gömbhöz. Mivel a gömbhéjon elhelyezkedő kvaterniókkal leírhatóak forgatások a háromdimenziós térben (egy előjelig bezárólag), létezik egy szürjektív homomorfizmus és a speciális ortogonális forgatáscsoport között, melynek magja az halmaz, ahol az egységmátrixot jelöli. Mivel a kvaterniók identifikálhatóak a Clifford-algebra páros részével, így az megegyeztethető a spinorok egyik szimmetriacsoportjával, a spincsoporttal.
Az speciális unitér csoportok rendkívül hasznosak a részecskefizika standard modelljében, főleg az elektrogyenge kölcsönhatás leírásában, az pedig a kvantum-színdinamikában.[1]
Tulajdonságai
[szerkesztés]A speciális unitér csoport egy szigorúan valós Lie-csoport, melynek dimenziója egy valós sokaságként . Topológiai tulajdonságai közé tartozik, hogy kompakt és egyszerűen összefüggő.[2] Algebrailag besorolható az egyszerű Lie-csoportok közé,[3] tehát a csoport Lie-algebrája is egyszerű.[4]
A speciális unitér csoport centruma izomorf a ciklikus csoporthoz, mely olyan diagonális mátrixokat tartalmaz, melynek minden eleme az -edik komplex gyöke az 1-nek. Abban az esetben, amikor , az a csoport külső automorfizmuscsoportja, míg az külső automorfizmuscsoportja a triviális csoport.
Az ranggal rendelkező maximális tóruszok megadhatóak olyan diagonális mátrixok halmazaként, melynek determinánsa egy. Az Weyl-csoportja a szimmetrikus csoport .
Lie-algebrája
[szerkesztés]Az Lie-algebrája, jelölés szerint , az olyan antihermitikus komplex mátrixok halmaza, melyek nyoma nulla.[5] A Lie-algebra Lie-zárójele a mátrixok kommutátora. A részecskefizikában gyakran használnak egy alternatív definíciót, mely szerint a csoport Lie-algebrája a nulla-nyommal rendelkező hermitikus mátrixok halmaza, ellátva egy olyan Lie-zárójellel, ami a kommutátor megszorozva -vel. Az algebra dimenziója szintúgy .
Struktúrája
[szerkesztés]Az komplexifikációja az , mely az -es nyommentes komplex mátrixok algebrája.[6] Ennek Cartan-részalgebrái tehát nyommentes diagonális mátrixokat tartalmaznak,[7] melyek bármelyike megegyeztethető egy olyan vektorral -ben, amelyek komponenseinek összege nulla. A gyökrendszerében ezáltal a számok lehetséges permutációja található meg. Az egyszerű gyököket választhatjuk következőféleképpen:
Következtetésképpen, az csoport rangja , Dynkin-diagrammja pedig , melyet grafikusan egy taggal rendelkező lánccal jelölünk.[8] Az Lie-algebra Cartan-mátrixa a következő:
Az Weyl-csoportja (vagy Coxeter-csoportja) az szimmetrikus csoport, amely az -szimplex szimmetriacsoportja.
Ábrázoláselmélete
[szerkesztés]Mivel az egy egyszerűen összefüggő Lie-csoport, bármelyik ábrázolása (vagy reprezentációja) levezethető a csoporthoz tartozó Lie-algebra (vagy pedig annak komplexifikációjának[6]) ábrázolásaiból.[9] Mivel a csoport kompakt, így a Peter–Weyl-tétel kimondja, hogy az ábrázolásai felbonthatóak irreducibilis ábrázolások direkt összegeként. Továbbá, az csoport nem kommutatív, így léteznek olyan irreducibilis ábrázolásai, melyeknek egynél nagyobb a dimenziója.
Fundamentális ábrázolása
[szerkesztés]Egy adott Lie-csoport fundamentális ábrázolása a legkisebb dimenziós nemtriviális irreducibilis ábrázolása. Az algebra esetén ez az az ábrázolás, amely megmutatja, hogy az algebra hogyan hat a testre. Fizikában használt konvenció szerint az algebra generátorainak választhatjuk azokat a nyommentes hermitikus -mátrixokat, melyekre teljesül
ahol a Kronecker-deltát, pedig a szerkezeti tényezőket jelöli, melyek minden indexükben antiszimmetrikusak, míg a -vel jelölt állandók minden indexükben szimmetrikusak.
Következésképpen, a generátorok kommutátora a következő:
a megfelelő antikommutátor pedig:
A kommutátor a fizikusok által használt konvenció szerint úgy teljesíti a Lie-zárójelet definiáló feltételeket, ha tartalmazza az imaginárius egységet, matematikai irodalomban nem található meg, mivel ott a generátorok antihermitikus mátrixok.
Általában a következő normalizáció használatos:
A generátorok teljesítik a Jabobi-identitást[10]:
A fizikusok által használt konvenció oka az, hogy így egyszerűbben leírhatók a fundamentális részecskék bizonyos tulajdonságai, mivel például esetén generátorként választhatók a Pauli-mátrixok -del megszorozva, továbbá az csoportnál a Gell-Mann-mátrixok szintén egy ketteddel megszorozva.[10] Ezen definíciók szerint a generátorok a következőt teljesítik:
Adjungált ábrázolása
[szerkesztés]Egy adott Lie-algebra adjungált ábrázolása az az ábrázolása, melyben az önmagára vetett (Lie-zárójel általi) hatása mutatkozik meg. Ebben az esetben a generátorok olyan -es mátrixok, melyeket a szerkezeti tényezők definiálnak:
Az SU(2) csoport
[szerkesztés]Az olyan -es unitér mátrixok csoportja, melyek determinánsa egy. Pontosabban kifejezve:
ahol például az komplex konjugáltját jelöli. A csoportművelet a mátrixszorzás.[11]
Kapcsolata a 3-gömbbel
[szerkesztés]Ha a definícióban szereplő és komplex számokat felbontjuk valós és imaginárius részeikre, tehát , akkor a determinánsra szabott feltétel a következő egyenlet lesz:
Ez pontosan az egységsugarú 3-gömb () egyenlete. Ezt a megfeleltetést lehet egy beágyazásnak is tekinteni: a leképezés
ahol a -es komplex mátrixok halmazát jelöli, egy valós injektív lineáris leképezés. Tehát, -nek a -ra vett korlátozása a 3-gömb beágyazása egy kompakt részsokaságába, pontosabban .
Ennek következtében, diffeomorf -vel, mely bizonyítja, hogy egyszerűen összefüggő, pedig ellátható egy olyan struktúrával, mely egy kompakt, összefüggő Lie-csoporttá teszi.
Kapcsolata az egységkvaterniókkal és a térbeli forgatásokkal
[szerkesztés]Az egységhosszú kvaterniókat röviden egységkvaternióknak hívjuk, és az csoportot generálják. Az általánosan megadott mátrix
leképezhető a következő formájú kvaternióba:
Ez a leképezés egy csoportizomorfizmus, a mátrix determinánsa pedig pontosan a kvaternió normája, tehát izomorf az egységkvaterniók csoportjához.[12]
Minden egységkvaternió megfelel egy háromdimenziós térbeli forgatásnak, az egységkvaterniók szorzata pedig a hozzájuk tartozó forgatások kompozíciójának. Továbbá, bármely háromdimenziós térbeli forgatás pontosan kettő különböző egységkvaternióval írható le. Pontosabban megfogalmazva létezik egy 2:1 szürjektív homomorfizmus és között. Ennek következtében, izomorf az faktorcsoporthoz, az univerzális fedése, továbbá az -at definiáló sokaság létrehozható, ha antipodális pontjait megfeleltetjük egymásnak.
Lie-algebrája
[szerkesztés]Az csoport Lie-algebrájába azon -es antihermitikus mátrixok tartoznak, melyek nyoma nulla.[5] Pontosabban:
Ezt az algebrát a következő három mátrix generálja:
melyek a következő kommutációs relációkat teljesítik:
Ezek a generátorok szoros összefüggésben állnak a kvantummechanikában alkalmazott Pauli-mátrixokkal: és Ennek következtében az algebrával leírható a fundamentális részecskék (például elektronok) spinje.
Továbbá, a Lie-algebra ábrázolásainak segítségével levezethetőek az ábrázolásai.
Az SU(3) csoport
[szerkesztés]Az egy 8-dimenziós valós egyszerű Lie-csoport, mely olyan -as unitér mátrixokat tartalmaz, melyek determinánsa egy.
Topológiai tulajdonságai
[szerkesztés]Az csoport egyszerűen összefüggő és kompakt.[13] A csoport topológiai struktúrája megérthető abból a tulajdonságából, hogy tranzitív módon hat az egységgömbre a térben. A gömb bármelyik pontjának stabilizátora izomorf -vel, amely topológiailag a 3-gömb. Ebből következik, hogy egy fibrált nyaláb, melynek bázistere , fibruma (vagy rostja) pedig . Mivel a fibrum és a bázistér is egyszerűen összefüggő, ebből következik, hogy is egyszerűen összefüggő.[14]
Homotópiacsoportok hosszú egzakt sorozatát vizsgálva bizonyítható, hogy az csoport egy nemtriviális (csavart) -nyaláb bázistér felett.
Lie-algebrája
[szerkesztés]Az Lie-algebrája , amely a -as (fizikai konvenció szerint) hermitikus mátrixokat tartalmazza, melyek nyoma nulla. Az algebra generátorai a
mátrixok, ahol a Gell-Mann-mátrixokat jelöli, melyek a Pauli-mátrixok háromdimenziós megfelelői:
A Gell-Mann-mátrixok a következő kommutációs és antikommutációs szabálynak tesznek eleget:
ahol a Lie-algebra szerkezeti tényezőjeit jelöli. Ezek esetén a következők:
ahol olyan , melyek nem érhetőek el az előbb felsoroltak permutációjaként, automatikusan nullák. A szimmetrikus tényezők a következők:
Egy általános csoportelem, melyet egy -as hermitikus nyommentes mátrix generál, leírható a következő másodfokú mátrixpolinommal:[15][16]
ahol
Általánosított speciális unitér csoport
[szerkesztés]Adott test esetén definiálható az általánosított speciális unitér csoport , mely azon lineáris leképezések csoportja, melyek determinánsa egy és egy feletti -dimenziós vektortérhez tartoznak. Továbbá, ezek a leképezések változatlanul hagynak egy nemelfajuló, szeszkvilineáris formát, melynek szignatúrája . Az mező felcserélhető egy kommutatív gyűrűre, ebben az esetben viszont a vektortér felcserélődik egy szabad modulusra.
Amennyiben egy szignatúrával rendelkező[17] hermitikus mátrixot, akkor minden -re teljesül
Amennyiben a csoport -ként van jelölve bármiféle testre való utalás nélkül, akkor a test általában a komplex számtest .
SU(1,1)
[szerkesztés]Az egy fontos példája az általánosított speciális unitér csoportoknak. Definíció szerint a következő:
Ez a csoport izomorf az és a csoportokkal,[18] ahol a vesszővel elválasztott két szám annak a kvadratikus alaknak a szignatúrájára utal, melyet a csoport változatlanul hagy. A definícióban található kifejezés egy hermitikus forma, melyből egy izotropikus másodfokú forma lesz, ha a -t és -t a valós komponenseire felbontjuk.
A csoport egy korai formája a kokvaterniók egységgömbjeként mutatkozott meg. Legyen
A három mátrix szorzata a kétdimenziós egységmátrix, továbbá mind a három mátrix antikommutál, mint a kvaterniók esetében. Továbbá, ugyanúgy az egységmátrix -szeresének négyzetgyöke, azonban . Mind a kvaterniók, mind a kokvaterniók esetén a skalármennyiségek többszöröseinek tekinthetők, így a továbbiakban a szakaszban az jelölés lesz alkalmazva.
A kokvaternió (ahol egy skalár) konjugáltja , hasonlóan a kvaterniókhoz. Az általuk definiálható másodfokú forma A kokvaterniók egységgömbjében ez a mennyiség 1, mely így pontosan megfeleltethető az csoportnak, ha a definícióban használt és komplex számokat felbontjuk valós és imaginárius részükre.
Fontos részcsoportok
[szerkesztés]A speciális unitér csoportot a fizikában fermionrendszerek szimmetriáinak leírására alkalmazzák. A spontán szimmetriasértés elméletében fontos bizonyos részcsoportjait felismerni. Például, a nagy egyesített elméletben jelentős részcsoportok esetén
ahol a a direkt szorzatot jelöli, pedig a körcsoport, mely olyan komplex számokat tartalmaz, melyek normája egy.
Bizonyos ortogonális és szimplektikus csoportok is részcsoportjai -nek:
Az részcsoportja a következő Lie-csoportoknak:
A következő izomorfizmusok gyakran használatosak: .[19]
Jelentősége a fizikában
[szerkesztés]Az az egyik legfontosabb szimmetriacsoport a fizikában. Az leírja a perdületet a kvantummechanikában, ezáltal a spint is. A csoport irreducibilis ábrázolásait egyedi módon karakterizálják a Casimir-operátor sajátértékei, ebből levezethető, hogy a spin vagy egész szám, vagy egy egész szám fele: például az elektron spinje 1/2 vagy -1/2 lehet, (a Planck-állandót elméleti fizikai konvenció szerint eggyel egyenlővé tesszük) a Pauli-mátrixok pedig a fundamentális ábrázolás generátorai. Mivel az csoportnak három generátora van, így az adjugált ábrázolása háromdimenziós: ez a spin-1 részecskéket írja le.
Az csoport a részecskefizikában a színtöltést írja le: itt két Casimir-operátor van és az irreducibilis ábrázolásokat egy számpárral lehet identifikálni. Továbbá, az segítségével osztályozhatók azok a hadronok, melyek könnyű (azaz top, down és strange) kvarkokból állnak.
Az önmagával vett direkt szorzata (tehát ) a relativisztikus kvantumelméletben is használt ortokrón Lorentz-csoport univerzális fedése.[20]
Jegyzetek
[szerkesztés]- ↑ Halzen, Francis; Martin, Alan. Quarks & Leptons: An Introductory Course in Modern Particle Physics. John Wiley & Sons (1984). ISBN 0-471-88741-2
- ↑ Hall 2015, Proposition 13.11
- ↑ Az egyszerű Lie-csoport olyan Lie-csoport, melynek nincs összefüggő nem-triviális normálosztója.
- ↑ Wybourne, B.G.. Classical Groups for Physicists. Wiley-Interscience (1974). ISBN 0471965057
- ↑ a b Hall 2015 Proposition 3.24
- ↑ a b Hall 2015 Section 3.6
- ↑ Hall 2015 Section 7.7.1
- ↑ Hall 2015 Section 8.10.1
- ↑ Hall 2015 Theorem 5.6
- ↑ a b Georgi, Howard. Lie Algebras in Particle Physics: From Isospin to Unified Theories, 1 (angol nyelven), Boca Raton: CRC Press. DOI: 10.1201/9780429499210 (2018. május 4.). ISBN 978-0-429-49921-0
- ↑ Hall 2015 Exercise 1.5
- ↑ Savage, Alistair: LieGroups
- ↑ Hall 2015 Proposition 13.11
- ↑ Hall 2015 Section 13.2
- ↑ Rosen, S P (1971). „Finite Transformations in Various Representations of SU(3)”. Journal of Mathematical Physics 12 (4), 673–681. o. DOI:10.1063/1.1665634.
- ↑ Curtright, T L; Zachos, C K (2015). „Elementary results for the fundamental representation of SU(3)”. Reports on Mathematical Physics 76 (3), 401–404. o. DOI:10.1016/S0034-4877(15)30040-9.
- ↑ Tehát p pozitív és q negatív sajátértéke van.
- ↑ Gilmore, Robert. Lie Groups, Lie Algebras and some of their Applications. John Wiley & Sons, 52, 201−205. o. (1974)
- ↑ Jost, Jürgen. Riemannian Geometry and Geometric Analysis. Springer Verlag (2002). ISBN 3-540-42627-2
- ↑ Gernot Eichmann: QCD and Hadron Physics (Lecture Notes). (Hozzáférés: 2024. október 30.)
Fordítás
[szerkesztés]Ez a szócikk részben vagy egészben a Special unitary group című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Források
[szerkesztés]- Hall, Brian C.. Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, 2nd, Graduate Texts in Mathematics, Springer (2015). ISBN 978-3319134666
Lásd még
[szerkesztés]- Az SU(2) ábrázoláselmélete részletesebben az angol Wikipédián
- Clebsch–Gordan-együtthatók az SU(3) ábrázoláselméletéhez az angol Wikipédián




































![{\displaystyle ~\left[T_{a},\,T_{b}\right]~=~i\sum _{c=1}^{n^{2}-1}\,f_{abc}\,T_{c}\;,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3405ac2cc1d7c8341f86701bf0112a8922ac3ffe)


![{\displaystyle [T_{a},[T_{b},T_{c}]]+[T_{b},[T_{c},T_{a}]]+[T_{c},[T_{a},T_{b}]]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d13b4aac12698770cefc03cda97884c5d6d9501)












![{\displaystyle {\begin{aligned}\varphi \colon \mathbb {C} ^{2}\to {}&\operatorname {M} (2,\mathbb {C} )\\[5pt]\varphi (\alpha ,\beta )={}&{\begin{pmatrix}\alpha &-{\overline {\beta }}\\\beta &{\overline {\alpha }}\end{pmatrix}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9d540cf990ed87348dc38f038644938711ce2ed)








![{\displaystyle \left[u_{3},u_{1}\right]=2\ u_{2},\quad \left[u_{1},u_{2}\right]=2\ u_{3},\quad \left[u_{2},u_{3}\right]=2\ u_{1}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2da532e2434fd294dbca0834da6f8192eb1dc480)









![{\displaystyle {\begin{aligned}\lambda _{1}={}&{\begin{pmatrix}0&1&0\\1&0&0\\0&0&0\end{pmatrix}},&\lambda _{2}={}&{\begin{pmatrix}0&-i&0\\i&0&0\\0&0&0\end{pmatrix}},&\lambda _{3}={}&{\begin{pmatrix}1&0&0\\0&-1&0\\0&0&0\end{pmatrix}},\\[6pt]\lambda _{4}={}&{\begin{pmatrix}0&0&1\\0&0&0\\1&0&0\end{pmatrix}},&\lambda _{5}={}&{\begin{pmatrix}0&0&-i\\0&0&0\\i&0&0\end{pmatrix}},\\[6pt]\lambda _{6}={}&{\begin{pmatrix}0&0&0\\0&0&1\\0&1&0\end{pmatrix}},&\lambda _{7}={}&{\begin{pmatrix}0&0&0\\0&0&-i\\0&i&0\end{pmatrix}},&\lambda _{8}={\frac {1}{\sqrt {3}}}&{\begin{pmatrix}1&0&0\\0&1&0\\0&0&-2\end{pmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27272365d50c95972a5a66b020caf63b836131df)
![{\displaystyle {\begin{aligned}\left[T_{a},T_{b}\right]&=i\sum _{c=1}^{8}f_{abc}T_{c},\\\left\{T_{a},T_{b}\right\}&={\frac {1}{3}}\delta _{ab}I_{3}+\sum _{c=1}^{8}d_{abc}T_{c},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c84522e4ae5ab8f237d70c19f62e7b45affdb3c3)




![{\displaystyle {\begin{aligned}\exp(i\theta H)={}&\left[-{\frac {1}{3}}I\sin \left(\varphi +{\frac {2\pi }{3}}\right)\sin \left(\varphi -{\frac {2\pi }{3}}\right)-{\frac {1}{2{\sqrt {3}}}}~H\sin(\varphi )-{\frac {1}{4}}~H^{2}\right]{\frac {\exp \left({\frac {2}{\sqrt {3}}}~i\theta \sin(\varphi )\right)}{\cos \left(\varphi +{\frac {2\pi }{3}}\right)\cos \left(\varphi -{\frac {2\pi }{3}}\right)}}\\[6pt]&{}+\left[-{\frac {1}{3}}~I\sin(\varphi )\sin \left(\varphi -{\frac {2\pi }{3}}\right)-{\frac {1}{2{\sqrt {3}}}}~H\sin \left(\varphi +{\frac {2\pi }{3}}\right)-{\frac {1}{4}}~H^{2}\right]{\frac {\exp \left({\frac {2}{\sqrt {3}}}~i\theta \sin \left(\varphi +{\frac {2\pi }{3}}\right)\right)}{\cos(\varphi )\cos \left(\varphi -{\frac {2\pi }{3}}\right)}}\\[6pt]&{}+\left[-{\frac {1}{3}}~I\sin(\varphi )\sin \left(\varphi +{\frac {2\pi }{3}}\right)-{\frac {1}{2{\sqrt {3}}}}~H\sin \left(\varphi -{\frac {2\pi }{3}}\right)-{\frac {1}{4}}~H^{2}\right]{\frac {\exp \left({\frac {2}{\sqrt {3}}}~i\theta \sin \left(\varphi -{\frac {2\pi }{3}}\right)\right)}{\cos(\varphi )\cos \left(\varphi +{\frac {2\pi }{3}}\right)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3911db5c2d7bd1d44edad1dff8db8099b077ed6)
![{\displaystyle \varphi \equiv {\frac {1}{3}}\left[\arccos \left({\frac {3{\sqrt {3}}}{2}}\det H\right)-{\frac {\pi }{2}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3b54c3b30a637ef4902d486f9d86c0a7e46db78)