Véges csoport

A csoportelméletben véges csoportnak nevezünk egy olyan csoportot, melynek alaphalmaza véges. Véges csoportok gyakran állnak elő matematikai vagy fizikai objektumok szimmetriájának vizsgálatakor, amikor ezek az objektumok csak véges számú struktúra-megőrző transzformációt engednek meg. Fontos példái a ciklikus csoportok és a szimmetrikus csoportok.

A véges csoportok tanulmányozása a csoportelmélet fontos része a 19. századi megjelenése óta. Az egyik legfontosabb részterülete a véges egyszerű csoportok osztályozása, mely 2004-ben fejeződött be arra az esetre, amikor a véges csoportnak nincs nemtriviális normálosztója.^[1]^[2]^[a]

Példák

Szimmetrikus és permutációcsoportok

Az $S_{n}$ -nel jelölt szimmetrikus csoport $n$ darab szimbólum összes permutációját tartalmazza, a csoportművelet pedig a permutációk kompozíciója, mely tekinthető a szimbólumok között egy bijektív függvényként.^[4] Mivel $n$ elemnek $n!$ ( $n$ faktoriális) lehetséges permutációja van, az $S_{n}$ csoport rendje (tehát elemeinek száma) $n!$ .

Ciklikus csoportok

Bővebben: Ciklikus csoport

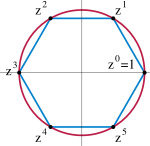
A $\mathbb {Z} _{n}$ ciklikus csoport minden eleme egy adott $a$ elem egész kitevős hatványa, ahol $a^{n}=a^{0}=e$ ( $e$ itt a csoport egységeleme). Az $n$ (véges) elemszámú ciklikus csoportok izomorfak a komplex egység $n$ -edik egységgyökeinek csoportjához.

Véges Abel-csoportok

Abel-csoportnak vagy kommutatív csoportnak hívunk egy olyan csoportot, melyben bármely csoportbeli elempáron végzett csoportművelet eredményén nem változtat a két elem felcserélése. Ezt a tulajdonságot a kommutativitás axiómájának is hívjuk.

Egy tetszőleges véges Abel-csoport izomorf olyan véges ciklikus csoportok direkt összegével, melyek elemszámai prímszámok egész kitevős hatványai és egyértelműen meghatározottak. A rendek invariánsok rendszerét alkotják, melyek leírják a véges Abel-csoport automorfizmuscsoportját. A véges Abel-csoportok elméletének fontos kezdőpontja Ferdinand Georg Frobenius és Ludwig Stickelberger 1879-es eredménye, amelyet később leegyszerűsítettek és általánosítottak, ezáltal fontos részét képezve a lineáris algebrának.

Lie-típusú csoportok

A Lie-típusú csoportok nem összetévesztendőek a Lie-csoportokkal, azonban szoros összefüggés van a két fogalom között. A Lie-csoportok olyan csoportok, melyek egyszerre sima sokaságok és a csoportművelet tetszőlegesen sokszor differenciálható. Egy kompakt Lie-csoport megfeleltethető a valós számtesten definiált reduktív lineáris algebrai csoport racionális pontjainak. Ha a valós számtestet felcseréljük egy véges testre, az általa definiált reduktív lineáris algebrai csoport racionális pontjainak csoportja szorosan kapcsolódik a Lie-típusú csoportokhoz. Önmagában a Lie-típusú csoportoknak nincs precíz széles körben elfogadott definíciója,^[5] azonban azoknak a véges egyszerű Lie-típusú csoportoknak van, melyek elősegítik a véges egyszerű csoportok osztályozását.

Véges Lie-típusú csoportok adják a nem-Abel véges egyszerű csoportok túlnyomó többségét. Speciális esetei a klasszikus csoportok, a Chevalley-csoportok, a Steinberg-csoportok és a Suzuki−Ree-csoportok.

Fontosabb tételek

Lagrange-tétel

A Joseph Louis Lagrange után elnevezett tétel kimondja, hogy egy adott $G$ véges csoport bármely $H$ részcsoportjának rendje (tehát az alaphalmaz elemeinek száma) osztója $G$ rendjének. Jelöljük $G$ rendjét $|G|$ -vel, akkor a $|G|/|H|$ természetes számot a $H$ részcsoport indexének hívjuk, jelölése $[G:H]$ . A részcsoport indexe a baloldali mellékosztályai számának felel meg.

A tétel következménye, hogy $G$ bármely $g$ elemének rendje (tehát egy olyan $n$ természetes szám, melyre $g^{n}=e$ , ahol $e$ a csoport egységeleme) mindig osztja a csoport rendjét.^[6]

Sylow-tételek

Bővebben: Csoportelmélet#Sylow-csoportok

Legyen $p$ egy prímszám. Egy adott $G$ csoport Sylow $p$ -részcsoportjának hívjuk bármely olyan részcsoportját, mely egy $p$ -csoport, tehát minden elemének rendje $p$ egy hatványa, és nem valódi részcsoportja $G$ bármelyik másik $p$ -részcsoportjának.

A Peter Ludwig Sylowról elnevezett tételek rendkívül fontosak a véges csoportok vizsgálatában, ugyanis részletes információt adnak egy fixált rendű véges csoport részcsoportjainak számáról. Tekinthető a Lagrange-tétel részleges megfordításának, mivel kimondja, hogy egy $G$ véges csoport rendjének minden prímtényezőjére létezik egy Sylow $p$ -részcsoportja $G$ -nek. Továbbá, $G$ minden $p^{n}$ rendű részcsoportja Sylow $p$ -részcsoport, és fixált $p$ prím esetén a csoport Sylow $p$ -részcsoportjai egymás konjugáltjai. Egy csoport Sylow $p$ -részcsoportjainak számát $p$ -vel osztva mindig egy lesz a maradék.^[7]

Cayley-tétel

Az Arthur Cayleyről elnevezett tétel kimondja, hogy bármely $n$ elemű $G$ csoport izomorf az $S_{n}$ szimmetrikus csoport valamilyen részcsoportjával. Pontosabban megfogalmazva, a szimmetrikus csoport elemei a $G$ alaphalmazának permutációi.^[8] Vannak esetek, amikor $G$ izomorf egy kisebb szimmetrikus csoport részcsoportjával, mint például a hatelemű $S_{3}$ nem csak $S_{6}$ egy részcsoportjával izomorf, hanem triviálisan önmagának részcsoportja is.^[9] Egy adott csoportra megtalálni a legkisebb szimmetrikus csoportot, melynek egy részcsoportjával izomorf egy önmagában nehéz feladat.^[10]^[11]

A tétel értelmezhető a $G$ csoporthatásának önmagának elemeire,^[12] továbbá kiterjeszthető végtelen csoportokra is.

Burnside-tétel

A Burnside-tétel kimondja, hogy amennyiben $G$ egy $p^{a}q^{b}$ elemszámú csoport, ahol $p$ és $q$ prímszámok, $a$ és $b$ pedig nemnegatív egész számok, akkor $G$ feloldható. A tételből következik, hogy bármely nem-Abel véges egyszerű csoport rendje osztható legalább három egymástól különböző prímszámmal.^[13]

Feit–Thompson-tétel

Bővebben: Feit–Thompson-tétel

A Feit–Thompson-tétel szerint bármely páratlan rendű csoport feloldható. A tételt Walter Feit és John G. Thompson bizonyította.^[14]

Osztályozása

A véges egyszerű csoportok osztályozásának tétele szerint minden véges egyszerű csoport a következők egyikébe tartozik:

Olyan ciklikus csoport, melynek rendje prímszám,
Legalább ötödfokú alternáló csoport,
Egyszerű Lie-típusú csoport,
A 26 sporadikus egyszerű csoport egyike,
A Tits-csoport (esetenként a 27. sporadikus csoportnak tekinthető)

A véges egyszerű csoportok olyan értelemben alkotják bármely véges csoport alapköveit, ahogy a prímszámok "építik fel" a természetes számok bármelyikét. A Jordan–Hölder-tétel precízen megfogalmazza ezt az elképzelést, azonban fontos megjegyezni, hogy véges egyszerű csoportok "összerakása" nem határoz meg egyértelműen egy véges csoportot, ugyanis létezhetnek nem-izomorf csoportok, melyeknek egyezik a kompozíciólánca.

Adott rendű csoportok száma

Adott $n$ pozitív egész számra nem mindig magától értetődő, hogy hány $n$ elemszámú csoport létezik izomorfiáig bezárólag. A következő esetek azonban megkönnyítik a klasszifikációt:

A Lagrange-tételből következik, hogy minden olyan csoport ciklikus, melynek rendje egy prímszám, ugyanis a csoport bármely nemneutrális eleme olyan részcsoportot generál, mely egyenlő az egész csoporttal.
Ha $n$ egy prímszám négyzete, akkor pontosan kettő nem-izomorf $n$ -edrendű csoport van, és mindkettő Abel.

Rend n	Csoportok száma^[15]	Ezek közül Abel^[16]	Ezek közül nem-Abel
0	0	0	0
1	1	1	0
2	1	1	0
3	1	1	0
4	2	2	0
5	1	1	0
6	2	1	1
7	1	1	0
8	5	3	2
9	2	2	0
10	2	1	1
11	1	1	0
12	5	2	3
13	1	1	0
14	2	1	1
15	1	1	0
16	14	5	9
17	1	1	0
18	5	2	3
19	1	1	0
20	5	2	3
21	2	1	1
22	2	1	1
23	1	1	0
24	15	3	12
25	2	2	0
26	2	1	1
27	5	3	2
28	4	2	2
29	1	1	0
30	4	1	3

Megjegyzések

↑ Az osztályozás 2008-ban mindenesetre egy korábbi kisebb hiba miatt tovább bővült.^[3]

Jegyzetek

↑ Aschbacher, Michael; Smith, Stephen D. (2004). „The classification of quasithin groups. I: Structure of strongly quasithin K-groups”. Mathematical Surveys and Monographs 111, Kiadó: Americal Mathematical Society.
↑ Aschbacher, Michael; Smith, Stephen D. (2004). „The classification of quasithin groups. II: Main theorems: the classification of simple QTKE-groups”. Mathematical Surveys and Monographs 112, Kiadó: Americal Mathematical Society.
↑ Harada, Koichiro; Solomon, Ronald (2008). „Finite groups having a standard component L of type M₁₂ or M₂₂”. Journal of Algebra 319 (2), 621–628. o. ISSN 0021-8693.
↑ Jacobson, Nathan. Basic Algebra I, 2.kiadás, Dover Publications, 31. o. (2009). ISBN 978-0-486-47189-1
↑ mathoverflow – Definition of “finite group of Lie type”?
↑ https://www.cs.bme.hu/~szeszler/bsz2/csoport.pdf
↑ Sylow, L. (1872. december 7.). „Théorèmes sur les groupes de substitutions” (francia nyelven). Math. Ann. 5 (4), 584–594. o. DOI:10.1007/BF01442913.
↑ Jacobson, Nathan. Basic Algebra I, 2.kiadás, Dover Publications, 38. o. (2009). ISBN 978-0-486-47189-1
↑ Cameron, Peter J.. Introduction to Algebra, Second Edition. Oxford University Press, 134]. o. (2008). ISBN 978-0-19-852793-0
↑ Johnson, D. L. (1971). „Minimal Permutation Representations of Finite Groups”. American Journal of Mathematics 93 (4), 857–866. o. DOI:10.2307/2373739. JSTOR 2373739.
↑ Grechkoseeva, M. A. (2003). „On Minimal Permutation Representations of Classical Simple Groups”. Siberian Mathematical Journal 44 (3), 443–462. o. DOI:10.1023/A:1023860730624.
↑ Jacobson, Nathan. Basic Algebra I, 2.kiadás, Dover Publications, 72. o. (2009). ISBN 978-0-486-47189-1
↑ Burnside, W. (1904). „On Groups of Order p^αq^β”. Proceedings of the London Mathematical Society (s2-1 (1)), 388–392. o. DOI:10.1112/plms/s2-1.1.388.
↑ Solvability of groups of odd order. [2016. március 4-i dátummal az eredetiből archiválva]. (Hozzáférés: 2018. július 23.)
↑ Humphreys, John F.. A Course in Group Theory. Oxford University Press, 238–242. o. (1996). ISBN 0198534590
↑ Number of Abelian groups of order n; number of factorizations of n into prime powers.. The On-Line Encyclopedia of Integer Sequences

Fordítás

Ez a szócikk részben vagy egészben a Finite group című angol Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Matematikaportál • összefoglaló, színes tartalomajánló lap

[4] Az osztályozás 2008-ban mindenesetre egy korábbi kisebb hiba miatt tovább bővült.^[3]

[1] Aschbacher, Michael; Smith, Stephen D. (2004). „The classification of quasithin groups. I: Structure of strongly quasithin K-groups”. Mathematical Surveys and Monographs 111, Kiadó: Americal Mathematical Society.

[2] Aschbacher, Michael; Smith, Stephen D. (2004). „The classification of quasithin groups. II: Main theorems: the classification of simple QTKE-groups”. Mathematical Surveys and Monographs 112, Kiadó: Americal Mathematical Society.

[3] Harada, Koichiro; Solomon, Ronald (2008). „Finite groups having a standard component L of type M₁₂ or M₂₂”. Journal of Algebra 319 (2), 621–628. o. ISSN 0021-8693.

[5] Jacobson, Nathan. Basic Algebra I, 2.kiadás, Dover Publications, 31. o. (2009). ISBN 978-0-486-47189-1

[6] thoverflow – Definition of “finite group of Lie type”?

[7] ttps://www.cs.bme.hu/~szeszler/bsz2/csoport.pdf

[8] Sylow, L. (1872. december 7.). „Théorèmes sur les groupes de substitutions” (francia nyelven). Math. Ann. 5 (4), 584–594. o. DOI:10.1007/BF01442913.

[9] Jacobson, Nathan. Basic Algebra I, 2.kiadás, Dover Publications, 38. o. (2009). ISBN 978-0-486-47189-1

[10] Cameron, Peter J.. Introduction to Algebra, Second Edition. Oxford University Press, 134]. o. (2008). ISBN 978-0-19-852793-0

[11] Johnson, D. L. (1971). „Minimal Permutation Representations of Finite Groups”. American Journal of Mathematics 93 (4), 857–866. o. DOI:10.2307/2373739. JSTOR 2373739.

[12] Grechkoseeva, M. A. (2003). „On Minimal Permutation Representations of Classical Simple Groups”. Siberian Mathematical Journal 44 (3), 443–462. o. DOI:10.1023/A:1023860730624.

[13] Jacobson, Nathan. Basic Algebra I, 2.kiadás, Dover Publications, 72. o. (2009). ISBN 978-0-486-47189-1

[14] Burnside, W. (1904). „On Groups of Order p^αq^β”. Proceedings of the London Mathematical Society (s2-1 (1)), 388–392. o. DOI:10.1112/plms/s2-1.1.388.

[15] Solvability of groups of odd order. [2016. március 4-i dátummal az eredetiből archiválva]. (Hozzáférés: 2018. július 23.)

[16] Humphreys, John F.. A Course in Group Theory. Oxford University Press, 238–242. o. (1996). ISBN 0198534590

[17] Number of Abelian groups of order n; number of factorizations of n into prime powers.. The On-Line Encyclopedia of Integer Sequences

[1]

[2]

[a]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[3]

Sablon:Csoportelmélet m v sz Csoportelmélet
Csoport · Részcsoport · Normálosztó · Faktorcsoport · Csoporthatás · Csoporthomomorfizmus · Kommutátor · Mag · Képtér
Csoportfajták	Egyszerű · Véges · Végtelen · Folytonos · Multiplikatív · Additív · Abel · Nilpotens · Feloldható
Véges csoportok és fontos tételeik	Ciklikus csoport Z_n Szimmetrikus csoport S_n Alternáló csoport A_n Diédercsoport D_n (Klein-csoport D₂) Kvaterniócsoport Q₈ p-csoport elemi Abel-csoport Frobenius-csoport Hall-részcsoport Schur-multiplikátor Cauchy-tétel Lagrange-tétel Sylow-tételek Feit–Thompson-tétel Véges egyszerű csoportok osztályozása: ciklikus, alternáló, Lie-típusú, sporadikus
Diszkrét csoportok és rácsok	Egész számok ( $\mathbb {Z}$ ) Szabad csoport Moduláris csoportok Aritmetikus csoport Hiperbolikus csoport
Topologikus és Lie-csoportok	Kör Általános lineáris GL(n) Speciális lineáris SL(n) Ortogonális O(n) Euklideszi E(n) Unitér U(n) Speciális ortogonális SO(n) Speciális unitér SU(n) Szimplektikus Sp(n) G₂ F₄ E₆ E₇ E₈ Lorentz Poincaré Konformális
Algebrai csoportok	Lineáris algebrai csoport Reduktív csoport Elliptikus görbe Abel-varietás