Wikipédia:Tudakozó/Archívum/2010-02-04

A Tudakozó főoldala • Én szeretnék választ adni! •  Archívum •  Eszmecsere a válaszadó önkéntesek között• Válaszadó sablonok •  TUGYIK

Egy szótárba illő kérdésnek, a szavak értelmezésének inkább a Wikiszótárban nézz utána.
A Wikipédia Tudakozójának önkéntesei vagyunk, és enciklopédiába, lexikonba való témákban igyekszünk választ adni. Megkérünk, hogy először a Wikipédia automatizált belső keresőjével próbáld a választ megkeresni, és csak ha ott nem találtad meg, akkor kattints ide, és tedd fel nekünk a kérdésedet!

A kérdésed (nem a válasz még!) egy-két perc elmúltával a mai kérdéseket tartalmazó lap alján fog látszani.
(Ha mégsem látszana, akkor próbáld meg a lapot a böngésződben frissíteni.)
Kérünk, hogy legyél türelemmel – itt mindenki a szabad idejét fordítja arra, hogy a segítségedre legyen.
Esetleg csak holnap, holnapután akad valaki, aki válaszolni tud neked, sőt néha még később írnak be egy választ a már archivált lapra.
Ha a mai lapot később keresed, ezt írd be a keresőablakba: Wikipédia:Tudakozó/Archívum/2025-01-05, vagy keresd az Archívumban.

A legutóbbi pár nap:

Wikipédia:Tudakozó/Archívum/2025-01-01 Négy napja

Wikipédia:Tudakozó/Archívum/2025-01-02 Három napja

Wikipédia:Tudakozó/Archívum/2025-01-03 Tegnapelőtt

Wikipédia:Tudakozó/Archívum/2025-01-04 Tegnap

Wikipédia:Tudakozó/Archívum/2025-01-05 Ma

2010. 2. 1. « 2010. 2. 2. « 2010. 2. 3. « 2010. 2. 4. » 2010. 2. 5. » 2010. 2. 6. » 2010. 2. 7.

Az űr hőmérséklete

WMAP kép a mikrohullámú háttérsugárzás (Cosmic Microwave Background CMB) egyenetlenségeiről (2003 június)

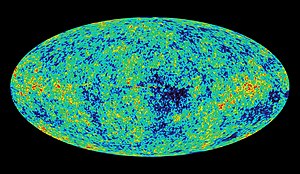
Megválaszolva. Ha további kiegészítést akarsz tenni, akkor kattints a szakaszcím mellett a [forrásszöveg szerkesztése] feliratra. Ha új kérdést akarsz feltenni, kattints ide!

Nohát. Szóval az a kérdés fészkelte be magát az elmémbe, hogy vajh az űrnek értelmezhető-e a hőmérséklete? A hőmérséklet szócikk azt mondja, hogy a kitöltő részecskék mozgási energiájáról beszélünk, a kérdés csupán az, hogy a háttérsugárzás fotonjai ilyen szempontból akkor részecskének számítanak-e? tetradumaláda 2010. február 4., 08:42 (CET)

válasz, Dencey-1:

• A világűr nagy részében uralkodó hőmérséklet 2,7 K, azaz −270°C. Ez a világűrt kitöltő kozmikus háttérsugárzás hatása, és az ősrobbanás mára fennmaradt nyomának, elektromágneses „visszhangjának” tekinthető. Ettől az értéktől régiónként eltérő hőmérséklet is mérhető, ahol az anyagsűrűség nagyobb.

Dencey ^vita 2010. február 4., 10:47 (CET)

nem hiszi-1, tetra:

A világűr szócikket én is el tudom ám olvasni (sőt, meg is tettem), de pont ezért tettem fel a kérdést, mert nem vagyok biztos benne, hogy ami a szócikkben szerepel, az korrekt.tetradumaláda 2010. február 4., 12:05 (CET)

válasz, Dencey-2:

Gondoltam, hogy elolvastad. Az angol nyelvű wiki a következőket írja "The current black body temperature of this photon radiation is about 3 K (−270 °C; −454 °F). Some regions of outer space can contain highly energetic particles that have a much higher temperature than the CMB." CMB = cosmic microwave background

Dencey ^vita 2010. február 4., 12:14 (CET)

válasz, LAndrás:

Hozzátenném, hogy a világűr nem abszolút üres tér, köbcentiméterenkénti egy részecskés átlagjával nagyon is értelmezhető a hőmérséklet és a mozgási energia közti összefüggés. L András^→ 2010. február 4., 10:53 (CET)

nem hiszi-2, tetra:

Természetesen nincs tökéletes vákum, de a galaxisközi térben kétlem, hogy meglenne az 1/köbcentis átlag. tetradumaláda 2010. február 4., 12:05 (CET)

visszakérdezés, vitorla:

Kedves kérdező! Milyen világűrbeli átlagsűrűség- és hőmérséklet-értéket fogadnál el? - vitorla^vita 2010. február 4., 21:19 (CET)

Tisztázás

Értelemszerűen, ha nincsenek részecskék, vagyis anyag, akkor nem tudunk közvetlenül valaminek a hőmérsékletéről beszélni. Viszont ha a tér mérendő pontjára (legyen az most egy galaxisközi hely) odateszünk egy fekete testet, akkor az a kozmikus sugárzás hatására kb. 2,7 Kelvin fokra fog felmelegedni. Ilyen értelemben beszélhetünk hőmérsékletről a világűrben a véleményem szerint. – Rodrigó ⇔ 2010. február 4., 21:55 (CET)

pontosítás:

Találomra körbenéztem. A csillagközi anyag című cikk megadja a világűr anyagsűrűségét némi számolgatással elérhető az eredmény. A hidrogénnek egy molja ~1 gramm (vagy 6·10²³ darab hidrogénatom), a csillagközi anyag átlagsűrűsége 10·10⁻²⁴ g/m³. L András^→ 2010. február 4., 22:19 (CET)

Megjegyzés:

Tetra, szerintem jobb kérdést tettél fel, mint amilyennek elsőre látszik. A fotont emlékezetem szerint nem nevezik részecskének, márpedig ha itt az űrben létrehoznánk egy darabka tökéletes vákuumot, majd a napfénynek kitéve odatennénk egy hőmérőt, én azt gondolom, hogy az szépen mutatná a száz foko(ka)t. Nekem, aki a fizikát nem eléggé magas fokon ismerem, nem tetszik a szócikk megfogalmazása. Azért sem, mert a részecskék kinetikus energiája egyszerűen mozgást jelent, az pedig mindig csak valamihez képest lehetséges. Ha egy egyenletes eloszlású részecskeáramba helyezve a hőmérőt olyan sebességgel és irányban mozgatnám, mint a részecskék áramlása, akkor hozzá képest nincs kinetikus energiája a részecskéknek, vagyis elértük volna az abszolút nulla fokot? Inkább talán a hőmozgásról lenne szó, de azt viszont meg kellene itt nevezni.

Az szintén megérne egy megjegyzést, hogy a Nap sugárzásának az űrben kitett hőmérő hogyan valósítsa meg egy objektív érték észlelését, és miként különíthető el, vagy miként foglalandó a szabályba az a hőmennyiség, amelyet maga a hőmérő elnyel. Mondhatjuk, hogy a Hold felszínén +130 fokos a hőmérséklet, de ez egy matt fekete papírba csomagolt vagy egy alufóliából kostruált gömbhéj belsejébe tett hőmérővel lesz mérhető?

Az anyagsűrűséggel kapcsolatos problémát jogosnak találom, és valóban lehet, hogy azokban a terekben, legyenek azok az űr akár tizedmilliméternyi méretű cellái, problémás a hőmérséklet definiálása. De nem kell apró cellákra korlátoznunk a kérdést (bár az is megfelel a vizsgálódásra), mert az L András által adott eredményt ha jól értelmezem, a csillagközi anyag sűrűsége 10 köbméterenként egy 1 atom. (A galaxisközi sűrűség, amire tetra is rákérdez, sokkal ritkább, gyaníthatóan.) Ha a mérés az onnan kiinduló hősugárzásra alapul. Ha a méréshez odateszünk egy hőmérőt, annak az anyagsűrűsége, mint ahogy a fekete testé, már értelmezhetővé teszi a hőmérsékletet. - Orion 8 ^vita 2010. február 5., 01:32 (CET)

kiegészítés, vitorla:

A foton: részecske. Ugyan nulla a tömege (a nyugalmi tömege), de ha ütközik egy elektronnal, akkor mozgásiránya, frekvenciája megváltozik (csökken) (a frekvenciája azért, mert a mutatkozó energiahiánya az elektroné lesz). Ez a jelenség az energia- és az impulzusmegmaradás feltételezésével megmagyarázható - ez csak úgy lehetséges, hogy a foton nemcsak hullámtermészetű valami, hanem részecske is.

A hőröl: nem kell misztifikálni. A hőérzet az ilyen hatást felfogni képes érzékszervekkel rendelkező élőlények sajátja. A hő - a fizika nézőpontjából - semmi más, mint mozgás. A részecskék mozgása. Az a bizonyos mozgás, amit hőmozgásnak szoktunk nevezni. Ne higgyük azt, hogy „egy egyenletes eloszlású részecskeáramba helyezve a hőmérőt olyan sebességgel és irányban mozgatnám, mint a részecskék áramlása, akkor hozzá képest nincs kinetikus energiája a részecskéknek” - de van! A részecskék mikroszkopikus, atomi méretű amplitudójú, véletlenszerűen minden irányú (statisztikusan nulla irányú) mozgása az a mozgás, ami a hőtan stúdiumának létjogosultságát adja: ez a hőmozgás - ez a makroszkopikus méretű részecskeáram fennállása esetén is mindig létezik, soha el nem enyészik, hiszen ez adja az áramló közeg hőmérsékletét. Annak a valószínűsége, hogy egy közegben minden részecske (és a mérőeszköz részecskéi is) a priori mozgása - akárcsak egy pillanatra is - teljesen azonos irányú és nagyságú legyen, egyszerűen szólva: lehetetlenül-végtelenül kicsi. Tehát nullától eltérő hőmérsékletet mindig fogunk mérni!

A részecskék mikroszkopikus mozgásának „sebességfokozata” a hőmérséklet. Ha a részecske nem mozog, akkor a hőmérséklete nulla. Vica versa. A természetben nulla hőmérsékletű részecske nincs, vagyis ahol részecske van, ott hőmérséklet is van. Ahol nincs részecske, ott mozgás nincs, tehát hő sincs, és hőmérséklet sincs. A hőmérő is részecskékből áll, tehát ahol mérünk, mindenképpen kell tapasztalnunk nemnulla hőmérsékletet. Ha nem akarunk „csalni” azzal, hogy a szinte „üres” közegbe egy - a helyzetet „meghamisító”, sok részecskéből álló - hőmérőt helyezünk, akkor nem marad más választásunk, mint az, hogy nem mérünk, hanem matematikázunk: meghosszabbítjuk a gáztörvény érvényességét a nulla sűrűségű tartományok felé. Ennek próbája az lesz, hogy a matematikázásból származó következtetéseket igazolni tudjuk!

A kérdezőnek semmit sem kell elhinnie. Véleményszabadság van. A fizikában is lehetne. Csak akkor ne mást vádoljon a katasztrófáért, ami akkor éri, amikor felmegy a Himalája tetejére: annak ellenére, hogy 8 km-rel közelebb van a Naphoz, mégis hidegebb van, mint a tengerszinten. Természetesen, sok minden más is szerepet játszik a hőmérsékletcsökkenésben, de pontosan azért kell bíznia a többévezredes emberi kollektíva felhalmozott ismereteiben, mert ebben a „szénakazalban” ott van a gáztörvény is, felismert korlátaival egyetemben - és ez a „szénakazal” egyre jobban működik! Vagyis, nem kell minden egyes törvény, megállapított szabály hatékonyságáról minden egyes földlakónak külön-külön, személyesen meggyőződnie!

vitorla^vita 2010. február 5., 11:01 (CET)

A hőérzet itt nem került szóba, magát a hőt firtattuk, amelynek a fizikai definíciója nekem nem felelt meg eléggé. Most sem, mármint a hőmérséklet szócikkben olvasható. Ott a hőmérséklet "az anyagot felépítő részecskék átlagos mozgási energiájával kapcsolatos mennyiség"-ként van leírva. A klasszikus fizikában a mozgási energia az, amit én leírtam. A hőmozgás, mivel az atomok hosszú távon ettől nem változtatják meg a helyüket, statisztikailag a nullához tartó mozgásienergia-változást jelent. Ami egyébként nem olyan döbbenetes dolog, ha úgy nézzük, hogy az anyag a betáplált energiát a hőmozgás során kisugározza; ha teljesen megszűnik az energiabevitel (fűtés), egy idő után lead minden hőmozgási energiát, és a hőmozgás leáll. Szóval a szócikk definícióját pontosítani kellene, mert nem mindegy, hogy a mozgási energia fajtáiból melyik jelenti a hőt. Megtenném én, ha eléggé benne lennék még a témában, de ha senki nem teszi meg, akkor egyszer majd megteszem én.

A gáztörvény "meghosszabbításának" bizonyító erejével kapcsolatban csak megemlítem a termoszféra hőmérsékletét, amely a felfelé csökkenő hőmérsékleti görbe meghosszabításával cseppet sem esik egybe. Ugyanilyen jellegű, noha teljesen más eredetű hőmérsékleti anomália vált ismertté a Nap középpontjától távolodva is. Ráadásul az abszolút nulla fok és az ahhoz igen közeli tartomány annyira speciális terület, amelyről megbízható kísérleti megfigyelések nélkül nyilatkozni kissé kockázatosnak tűnik. Alig több a hiedelmeknél. Az a görbe ott, a végén még akármit megcsinálhat.

"A kérdező" ez esetben vagy tetra volt, vagy én. Egyikünk sem olyan iskolázatlan, hogy értetlenkedve állnánk a Himaláján megfigyelhető alacsony hőmérsékleti értékek előtt. A több évezredes emberi kollektíva felhalmozott ismereteinek csúcsán pedig egy időben ott állt a sumér asztrológia is, csak később még több tudás halmozódott fel. Kisebb-nagyobb kerülőkkel. Nincs semmi okunk feltételezni, hogy a jelenlegi tudásunk nem gyarapodhat tovább ugrásszerű eredményekkel, sőt olyanokkal is akár, amelyek azt fogják a jövő civilizációinak igazolni, hogy most éppen benne járunk egy újabb kitérőben. A ptolemaioszi naprendszermodell is működött. Bizonyos pontosság felett lett látható az eltérés a modell matematikája által jósolt és a valóban mért értékek között. Így hát a matematikai eszközökkel készített modellek extrapolációs megbízhatóságáról érdemes óvatossággal nyilatkozni. - Orion 8 ^vita 2010. február 5., 23:05 (CET)

(Szerkesztési ütközés után) Némi keveredést érzek itt a sugárzási hőmérséklet és a kinetikus hőmérséklet között. A kettő nem mindig hasonlítható össze. A napkoronában például egymillió kelvin feletti kinetikus energiával rendelkeznek a részecskék, de attól még vígan meg lehetne ott fagyni a kis anyagsűrűség miatt (eltekintve a Nap közelségétől). A kozmikus háttérsugárzás hőmérséklete nem azt jelenti, hogy ilyenre melegítene egy nulla kelvines objektumot, hanem azt, hogy a sugárzás hullámhossza megegyezik egy 3 K hőmérsékletű fekete test sugárzásával. Ezért a kozmikus háttérsugárzásban nem is értelmezhető a vörös- vagy kékeltolódás, a hullámhossz ilyen változásai a sugárzási hőmérséklet apró egyenetlenségeit mutatja. (Vitorla megjegyzése után már szükségtelenné is vált ez a hozzászólásom) L András^→ 2010. február 5., 11:14 (CET)

A kinetikus hőmérséklet említése segítségemre volt, mert számomra ismeretlen volt ez a megnevezés. Ennek nyomán találtam A csillagok hőmérséklete című weboldalra, ahol ez részletesebben is körül van írva, ezt a még érdeklődőknek mondom. Ezek a meghatározások nekem kissé távol állnak a hő klasszikus mérhetőségétől, de sebaj. Az, amit a napkoronáról írtál, az az előtte általam emlegetett üres cellák hőmérsékletével látszik egybevágni, ami jelzi, hogy vannak itt gyakorlatias módon nehezen értelmezhető kérdések. A válaszokat én is köszönöm; ha még a Hold felszínén napfényben mért jóval 100°C feletti hőmérséklet mikéntjéről is írna valaki, az még szebb lenne. - Orion 8 ^vita 2010. február 5., 23:05 (CET)

Magyarország kereskedelmi kapcsolatai a múltban és jövőben

További információt szeretnénk a kérdezőtől. Beírhatod, ha a szakaszcím mellett a [forrásszöveg szerkesztése] feliratra kattintasz. Ha új kérdést akarsz feltenni, kattints ide!

sziasztok!

A kereskedelmi utakról szeretnék egy kicsit többet megtudni!

válaszotokat előre is köszönöm!

--188.36.31.217 (vita) 2010. február 4., 19:57 (CET)

Visszakérdezés, Karmela:

Túlságosan általánosan fogalmazva tetted fel ahhoz a kérdést, hogy itt az olvasószolgálat keretei között választ adhatnánk rá.

Ugye nem kivánod tőlünk, hogy kidolgozott érettségi tételeket hozzunk itt neked?

De ha van valami konkrétabb kérdésed, akkor tedd fel azt, és igyekszünk válaszolni rá.

Azokra a cikkekre is vethetsz egy pillantást, amiket a kereskedelmi út keresőkérdés kidob, például 63-as főút (Magyarország), Borostyánút, Pannonia (provincia), Keszthely, stb.

Karmela^üzenőlap 2010. február 4., 21:20 (CET)

Válasz

A Kategória:Magyar gazdaságtörténet lapjait ajánlom figyelmedbe. Továbbá fontos fogalom a Közlekedési vám, amelyet mindig a forgalmas csomópontokban szedtek. – Rodrigó ⇔ 2010. február 4., 22:02 (CET)