Test (geometria)

A geometriában test alatt olyan háromdimenziós alakzatokat értünk, amelyek határfelülettel jellemezhetőek. Néha szó esik magasabb dimenziós testekről is; ekkor azonban jelzik a dimenziót is. A határfelületet alkothatják sokszöglapok vagy görbült felületek. A legismertebb mértani testeket sokszög, körlap vagy gömbrész felületek határolják. Többek között a hengerek, a gömbök és a gúlák (speciálisan a tetraéderek és a piramisok) tartoznak az ismertebb mértani testek közé. Poliédernek nevezzük a testet, ha csak síkok határolják, ilyenek speciálisan a hasábok, és a kockák például. Sok mértani test felszíne, illetve térfogata kiszámítható képletekkel.
Ha a geometriai kontextus nem egyértelmű, akkor test szó helyett használják a mértani test vagy geometriai test összetételeket is; ugyanis a test szónak van egy másik, algebrai jelentése is.
Egy test konvex, ha bármely két pontja közötti szakasz is a test része. Konvex tehát például a gömb, de nem konvex a tórusz.
Definíciók
[szerkesztés]A mértani testekre többféleképpen is lehet gondolni. Ha a teret ponthalmazként értelmezzük, akkor a mértani testek ponthalmazok, melyek teljesítenek bizonyos tulajdonságokat. Ezt a különféle definíciók különféleképpen fejezik ki, megkövetelve, hogy a mértani test valóban véges, háromdimenziós, zárt alakzat legyen, melyet véges sok felület határol.
A térgeometriában a test korlátos zárt háromdimenziós alakzat a térben, melyet véges sok, sík vagy görbült felület határol. A korlátosság azt jelenti, hogy a ponthalmaz befoglalható egy elég nagy gömbbe. A határoló felületek uniója a test felszíne. A test felülete két részre bontja a teret. A test belseje az a térrész, mely nem tartalmaz egyenest.[1]
A geometriai modellezésben a test korlátos és reguláris részhalmaza a háromdimenziós térnek. Egy halmaz reguláris, ha megegyezik belsejének lezártjával. Ez a feltétel biztosítja, hogy a test tartalmazza a határát, és teljesen háromdimenziós, azaz nincsenek alacsonyabb dimenziós tartományai. Ezek szerint a testnek nem kell összefüggőnek lenni, állhat több, egymással össze nem függő darabból is.[2][3]
Egy test felszíne állhat több, egymással nem összefüggő darabból; például, ha üreges (nem tömör). Ha ezek a felületek irányítva vannak, akkor a test leírható felületével. Ekkor felszínábrázolásról van szó.
Típusok
[szerkesztés]
Az általános értelemben vett testekre példák: kocka, tetraéder, gúla, kúp, hasáb, henger, oktaéder, gömb, tórusz.
Ha egy test konvex, akkor konvex testnek nevezzük. A szabályos testek konvexek. A konvex test fogalma megfogalmazható normával is, például p-normával.
A poliédereket csak sokszöglapok határolják.
Forgástestek
[szerkesztés]Forgástestek azok a testek, melyek megkaphatók egy görbe tengely körüli elforgatásával. A tengellyel párhuzamos összes metszet kör vagy körgyűrű alakú. Erre példa a gömb, a henger, a gúla, a csonkagúla, a tórusz és a forgásellipszoid. A gömbnek tengelye minden egyenes, ami a középpontján megy keresztül.
Szabályos testek és társaik
[szerkesztés]Szabályos (vagy platóni) testnek olyan konvex testeket értünk, amelyeknek minden lapját egybevágó szabályos sokszögek alkotják, és ezek egyforma szögeket zárnak be. Szabályos test duálisa is szabályos test. Ezek közül csak a kockával lehet hiánytalanul kitölteni a teret.

|

|

|

|

|
| tetraéder | hexaéder | oktaéder | dodekaéder | ikozaéder |
|---|
Ezek általánosításai az arkhimédészi testek, a velük duális Catalan-testek és a Johnson-testek. Ezek közül csak a csonkolt oktaéderrel és a gyrobifastigiummal lehet hiánytalanul kitölteni a teret. Csak szabályos lapjaik vannak még a prizmáknak és az antiprizmáknak.
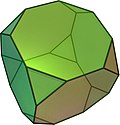
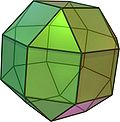
Arkhimédészi testek:

|

|
|

|
|
| csonkított tetraéder | kuboktaéder | csonkított kocka | csonkított oktaéder | kis rombikuboktaéder |
|---|

|

|

|

|

|
| csonkított kuboktaéder | pisze kocka | ikozidodekaéder | csonkított dodekaéder | csonkított ikozaéder |
|---|

|

|

|
| csonkított kuboktaéder | nagy rombikozidodekaéder | pisze dodekaéder |
|---|
|

|

|

|

|
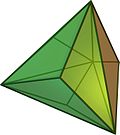
| triakisztetraéder | rombododekaéder | tetrakiszhexaéder | triakiszoktaéder | deltoidalikozitetraéder |
|---|

|

|

|

|

|
| pentagonikozitetraéder | hexakizoktaéder | rombitriakontaéder | pentakiszdodekaéder | triakiszikozaéder |
|---|

|

|

|
| deltoidalhexakontaéder | pentagonhexakontaéder | hexakiszikozaéder |
|---|
Johnson-testből 92 van. A prizmák speciális hasábok: egyenes hasábok, az alaplapjuk szabályos, palástjuk pedig négyzetekből áll. Uniform hasábnak is nevezik. Végtelen sorozatot alkotnak.
CSG
[szerkesztés]A mértani testek mind a háromdimenziós tér () részhalmazai, így a halmazműveletek minden további nélkül alkalmazhatóak rájuk. Mértani testek metszete, uniója és különbsége is mértani test. Ezt használják ki számítógépes szoftverek ray tracing alkalmazásokban és az ilyen konstrukciót nevezik idegen szóval CSG-nek a Constructive Solid Geometry rövidítéseként.

|

|

|
| Testek egyesítése (uniója) is test | Testek különbsége is test | Testek közös része (metszete) is test |
|---|
Fraktáltestek
[szerkesztés]| Ehhez a szócikkhez további forrásmegjelölések, lábjegyzetek szükségesek az ellenőrizhetőség érdekében. Emiatt nem tudjuk közvetlenül ellenőrizni, hogy a szócikkben szereplő állítások helytállóak-e. Segíts a szócikk fejlesztésében további megbízható források hozzáadásával. |

Általában azokat a testeket nevezik fraktáltesteknek, melyeknek térfogata nulla, felszíne végtelen. Ilyen testeket rendszerint rekurzívan, konvergens sorozatok határértékeként definiálnak. A konvergencia értelmezéséhez szükség van egy távolságfogalomra is a geometriai testek halmazán, amely gyakran a Hausdorff-metrika. Ismertebb fraktáltestek a következők:
- Menger-szivacs (A kétdimenziós Sierpinki-szőnyeg illetve az egydimenziós Cantor-halmaz általánosításaként.)
- Sierpinki-szivacs (A kétdimenziós Sierpinki-háromszög általánosításaként.)
Továbbiak
[szerkesztés]- A testek szemléltethetők hálójukkal, testmodellekkel és számítógépi alkalmazásokkal, például CAD alkalmazással és a dinamikus geometria eszközeivel.
- Sok testnek ismert a felszín- és a térfogatképlete.
- Egyes testek szimmetriái bevezetnek a csoportelméletbe.
- A kristályok elemi cellákból épülnek fel, melyek mértani testeknek tekinthetők.
Jegyzetek
[szerkesztés]- ↑ szerk.: Harri Deutsch: Fachlexikon ABC Mathematik. Thun/ Frankfurt am Main: Walter Gellert, Herbert Kästner, Siegfried Neuber (1998)
- ↑ Max K. Agoston. Computer Graphics and Geometric Modelling: Implementation & Algorithms. Springer (2005)
- ↑ Leila de Floriani, Enrico Puppo.szerk.: George Zobrist, C Y Ho: Representation and conversion issues in solid modelling. CRC Press (2000)
Források
[szerkesztés]- Hajnal Imre: Matematika IV., Budapest: Nemzeti Tankönyvkiadó, 1999, 47–133. oldal, ISBN 963-18-9326-X
- Tommy Bonnesen, W. Fenchel. Theorie der konvexen Körper. American Mathematical Soc. (1971)
Fordítás
[szerkesztés]Ez a szócikk részben vagy egészben a Körper (Geometrie) című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

