A trigonometrikus és hiperbolikus függvények, illetve ezek inverzei A hiperbolikus függvények a matematikában a szögfüggvényekhez hasonló függvények.
A két alapvető hiperbolikus függvény a hiperbolikus szinusz (jelölése sh vagy sinh ) és a hiperbolikus koszinusz (jelölése ch vagy cosh ), melyekből levezethető a hiperbolikus tangens (jelölése th vagy tanh ) függvény a szögfüggvényekhez hasonlóan. Ugyanúgy számolható belőlük a hiperbolikus szekáns és a hiperbolikus koszekáns , mint trigonometrikus megfelelőikből a szekáns és a koszekáns. Ezeknek a függvényeknek az inverzei az area hiperbolikus függvények . Ezt az adott függvény neve elé tett area szó jelzi. Mindezek a függvények egyes szerzőknél latin nevükkel szerepelnek, mint sinus hyperbolicus, cosinus hyperbolicus, tangens hyperbolicus, cotangens hyperbolicus, secans hyperbolicus, cosecans hyperbolicus; illetve az area függvények: area sinus hyperbolicus, area cosinus hyperbolicus, area tangens hyperbolicus, area cotangens hyperbolicus, area secans hyperbolicus, area cosecans hyperbolicus.
Ahogy a (cos t , sin t ) pontok egy kört határoznak meg, az az
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
t , sh t ) pontok egy hiperbola jobb oldali félgörbéjét írják le, mely az
x
2
−
y
2
=
1
{\displaystyle x^{2}-y^{2}=1}
(
i
y
)
2
=
−
y
2
{\displaystyle (iy)^{2}=-y^{2}}
cos
(
i
x
)
=
ch
x
{\displaystyle \cos(ix)=\operatorname {ch} x}
holomorf függvények . A többi hiperbolikus függvénynek pólusai vannak a képzetes tengelyen.
A hiperbolikus függvények azért is fontosak, mert több lineáris differenciálegyenlet megoldását fel lehet írni a használatukkal. Ilyen például derékszögű koordináta-rendszerben a súlya alatt lelógó kábel egyenlete.
Alkalmazhatóak ezen kívül a Laplace-egyenlet megoldásánál, amely a fizika több területén – az elektromágnesség elméletében, hőátadásban , folyadékok dinamikájában és a speciális relativitáselméletben – is fontos.
Az origóból kiinduló sugár az
x
2
−
y
2
=
1
{\displaystyle x^{2}-y^{2}=1}
(
ch
A
,
sh
A
)
{\displaystyle (\operatorname {ch} A,\operatorname {sh} A)}
A
{\displaystyle A}
x
{\displaystyle x}
Az egységhiperbola egyenlete
x
2
−
y
2
=
1
{\displaystyle x^{2}-y^{2}=1}
x
=
ch
(
t
)
,
y
=
sh
(
t
)
{\displaystyle x=\operatorname {ch} (t),y=\operatorname {sh} (t)}
Hasonló kapcsolatban állnak, mint a trigonometrikus függvények az egységkörrel:
x
=
cos
(
t
)
,
y
=
sin
(
t
)
:
x
2
+
y
2
=
1
{\displaystyle x=\cos(t),y=\sin(t):x^{2}+y^{2}=1}
Itt
sh
(
A
)
{\displaystyle \operatorname {sh} (A)}
y
{\displaystyle y}
ch
(
A
)
{\displaystyle \operatorname {ch} (A)}
x
{\displaystyle x}
th
(
A
)
{\displaystyle \operatorname {th} (A)}
y
{\displaystyle y}
x
=
1
{\displaystyle x=1}
Ha a területet integrálással számítjuk ki, akkor az exponenciális ábrázoláshoz jutunk, ami használható ekvivalens definícióként:
sh
(
z
)
:=
e
z
−
e
−
z
2
{\displaystyle \operatorname {sh} (z):={\frac {e^{z}-e^{-z}}{2}}}
ch
(
z
)
:=
e
z
+
e
−
z
2
{\displaystyle \operatorname {ch} (z):={\frac {e^{z}+e^{-z}}{2}}}
Ez alapján a hatványsorok:
sh
(
z
)
=
z
+
z
3
3
!
+
z
5
5
!
+
z
7
7
!
+
⋯
=
∑
n
=
0
∞
z
2
n
+
1
(
2
n
+
1
)
!
ch
(
z
)
=
1
+
z
2
2
!
+
z
4
4
!
+
z
6
6
!
+
⋯
=
∑
n
=
0
∞
z
2
n
(
2
n
)
!
,
{\displaystyle {\begin{aligned}\operatorname {sh} (z)&=z+{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}+{\frac {z^{7}}{7!}}+\dots =\sum _{n=0}^{\infty }{\frac {z^{2n+1}}{(2n+1)!}}\\\operatorname {ch} (z)&=1+{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}+{\frac {z^{6}}{6!}}+\dots =\sum _{n=0}^{\infty }{\frac {z^{2n}}{(2n)!}}\,,\end{aligned}}}
Itt
n
!
{\displaystyle n!}
n
{\displaystyle n}
n
{\displaystyle n}
cos
{\displaystyle \cos }
sin
{\displaystyle \sin }
Minden valós számra
sh
x
{\displaystyle \operatorname {sh} x}
ch
x
{\displaystyle \operatorname {ch} x}
A valós
sh
x
{\displaystyle \operatorname {sh} x}
valós szám ; a valós
ch
x
{\displaystyle \operatorname {ch} x}
A valós
sh
x
{\displaystyle \operatorname {sh} x}
A valós
ch
x
{\displaystyle \operatorname {ch} x}
(
−
∞
,
0
]
{\displaystyle (-\infty ,0]}
[
0
,
∞
)
{\displaystyle [0,\infty )}
x
=
0
{\displaystyle x=0}
A valós
sh
x
{\displaystyle \operatorname {sh} x}
a
1
(
x
)
=
1
2
e
x
,
x
→
∞
{\displaystyle a_{1}(x)={\frac {1}{2}}e^{x},\quad x\to \infty }
a
2
(
x
)
=
−
1
2
e
−
x
,
x
→
−
∞
{\displaystyle a_{2}(x)=-{\frac {1}{2}}e^{-x},\quad x\to -\infty }
ch
x
{\displaystyle \operatorname {ch} x}
a
1
(
x
)
=
1
2
e
x
,
x
→
∞
{\displaystyle a_{1}(x)={\frac {1}{2}}e^{x},\quad x\to \infty }
a
2
(
x
)
=
1
2
e
−
x
,
x
→
−
∞
{\displaystyle a_{2}(x)={\frac {1}{2}}e^{-x},\quad x\to -\infty }
Mivel
sh
,
ch
:
R
↦
R
{\displaystyle \operatorname {sh} ,\operatorname {ch} \colon \mathbb {R} \mapsto \mathbb {R} }
Az
sh
x
{\displaystyle \operatorname {sh} x}
ch
x
{\displaystyle \operatorname {ch} x}
A függvények periodikusak, periódusuk
2
π
i
{\displaystyle 2\pi i}
A következő szakaszok további összefüggéseket mutatnak be. Minden valós számra
th
x
{\displaystyle \operatorname {th} x}
cth
x
{\displaystyle \operatorname {cth} x}
cth
x
{\displaystyle \operatorname {cth} x}
A valós
th
x
{\displaystyle \operatorname {th} x}
−
1
<
f
(
x
)
<
1
{\displaystyle -1<f\left(x\right)<1}
cth
x
{\displaystyle \operatorname {cth} x}
{
−
∞
<
f
(
x
)
<
−
1
}
∪
{
1
<
f
(
x
)
<
+
∞
}
{\displaystyle \{-\infty <f\left(x\right)<-1\}\cup \{1<f\left(x\right)<+\infty \}}
A valós
th
x
{\displaystyle \operatorname {th} x}
x
=
0
{\displaystyle x=0}
inflexiós pont is.
A valós
th
x
{\displaystyle \operatorname {th} x}
cth
x
{\displaystyle \operatorname {cth} x}
x
<
0
{\displaystyle x<0}
x
>
0
{\displaystyle x>0}
Nem periodikus, páratlan függvények.
A valós
th
x
{\displaystyle \operatorname {th} x}
x
→
+
∞
:
f
(
x
)
→
+
1
{\displaystyle x\to +\infty \colon f\left(x\right)\to +1}
x
→
−
∞
:
f
(
x
)
→
−
1
{\displaystyle x\to -\infty \colon f\left(x\right)\to -1}
cth
x
{\displaystyle \operatorname {cth} x}
x
→
+
∞
:
f
(
x
)
→
+
1
{\displaystyle x\to +\infty \colon f\left(x\right)\to +1}
x
→
−
∞
:
f
(
x
)
→
−
1
{\displaystyle x\to -\infty \colon f\left(x\right)\to -1}
Minden valós számra
sech
x
{\displaystyle \operatorname {sech} x}
csch
x
{\displaystyle \operatorname {csch} x}
csch
x
{\displaystyle \operatorname {csch} x}
A valós
sech
x
{\displaystyle \operatorname {sech} x}
0
<
f
(
x
)
≤
1
{\displaystyle 0<f(x)\leq 1}
csch
x
{\displaystyle \operatorname {csch} x}
−
∞
<
f
(
x
)
<
+
∞
;
f
(
x
)
≠
0
{\displaystyle -\infty <f(x)<+\infty \,;\,f(x)\neq 0}
A valós
sech
x
{\displaystyle \operatorname {sech} x}
x
<
0
{\displaystyle x<0}
x
>
0
{\displaystyle x>0}
csch
x
{\displaystyle \operatorname {csch} x}
x
<
0
{\displaystyle x<0}
x
>
0
{\displaystyle x>0}
Nem periodikusak.
sech
x
{\displaystyle \operatorname {sech} x}
csch
x
{\displaystyle \operatorname {csch} x}
Mindkét függvénynek aszimptotája
f
(
x
)
→
0
{\displaystyle f(x)\to 0}
x
→
±
∞
{\displaystyle x\to \pm \infty }
A valós
sech
x
{\displaystyle \operatorname {sech} x}
x
=
0
{\displaystyle x=0}
csch
x
{\displaystyle \operatorname {csch} x}
A valós
sech
x
{\displaystyle \operatorname {sech} x}
x
=
±
ln
(
1
+
2
)
{\displaystyle x=\pm \ln {(1+{\sqrt {2}})}}
csch
x
{\displaystyle \operatorname {csch} x}
sh , ch és th csch , sch és cth A hiperbolikus függvények:
sh
x
=
e
x
−
e
−
x
2
=
−
i
sin
i
x
{\displaystyle \operatorname {sh} x={\frac {e^{x}-e^{-x}}{2}}=-i\sin ix\!}
ch
x
=
e
x
+
e
−
x
2
=
cos
i
x
{\displaystyle \operatorname {ch} x={\frac {e^{x}+e^{-x}}{2}}=\cos ix\!}
th
x
=
sh
x
ch
x
=
e
x
−
e
−
x
e
x
+
e
−
x
=
e
2
x
−
1
e
2
x
+
1
=
1
−
2
e
2
x
+
1
=
−
i
tg
i
x
{\displaystyle \operatorname {th} x={\frac {\operatorname {sh} x}{\operatorname {ch} x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}={\frac {e^{2x}-1}{e^{2x}+1}}=1-{\frac {2}{\mathrm {e} ^{2x}+1}}=-i\operatorname {tg} ix\!}
cth
x
=
ch
x
sh
x
=
e
x
+
e
−
x
e
x
−
e
−
x
=
e
2
x
+
1
e
2
x
−
1
=
1
+
2
e
2
x
−
1
=
i
ctg
i
x
{\displaystyle \operatorname {cth} x={\frac {\operatorname {ch} x}{\operatorname {sh} x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}}={\frac {e^{2x}+1}{e^{2x}-1}}=1+{\frac {2}{\mathrm {e} ^{2x}-1}}=i\operatorname {ctg} ix\!}
sch
x
=
1
ch
x
=
2
e
x
+
e
−
x
=
sec
i
x
{\displaystyle \operatorname {sch} x={\frac {1}{\operatorname {ch} x}}={\frac {2}{e^{x}+e^{-x}}}=\sec ix\!}
csch
x
=
1
sh
x
=
2
e
x
−
e
−
x
=
i
csc
i
x
{\displaystyle \operatorname {csch} x={\frac {1}{\operatorname {sh} x}}={\frac {2}{e^{x}-e^{-x}}}=i\,\csc \,ix\!}
ahol
i
{\displaystyle i}
imaginárius egység .
A fenti definíciókban a komplex alakok az Euler-formulából adódnak.
ch
2
x
−
sh
2
x
=
1
{\displaystyle \operatorname {ch} ^{2}x\!\;-\operatorname {sh} ^{2}x=1}
ch
x
+
sh
x
=
e
x
{\displaystyle \operatorname {ch} x\,\;+\operatorname {sh} x\,\,=e^{x}}
Euler-azonosság )
ch
x
−
sh
x
=
e
−
x
{\displaystyle \operatorname {ch} x\,\;-\operatorname {sh} x\,\,=e^{-x}}
ch
(
arsh
(
x
)
)
=
x
2
+
1
{\displaystyle \operatorname {ch} ({\operatorname {arsh} }(x))={\sqrt {x^{2}+1}}}
sh
(
arch
(
x
)
)
=
x
2
−
1
{\displaystyle \operatorname {sh} ({\operatorname {arch} }(x))={\sqrt {x^{2}-1}}}
sh
(
−
x
)
=
−
sh
x
{\displaystyle \operatorname {sh} (-x)=-\operatorname {sh} x\,\!}
ch
(
−
x
)
=
ch
x
{\displaystyle \operatorname {ch} (-x)=\operatorname {ch} x\,\!}
Innen:
th
(
−
x
)
=
−
th
(
x
)
{\displaystyle \operatorname {th} (-x)=-\operatorname {th} (x)\,\!}
cth
(
−
x
)
=
cth
(
x
)
{\displaystyle \operatorname {cth} (-x)=\operatorname {cth} (x)\,\!}
sch
(
−
x
)
=
sch
x
{\displaystyle \operatorname {sch} (-x)=\operatorname {sch} \,x\,\!}
csch
(
−
x
)
=
−
csch
x
{\displaystyle \operatorname {csch} (-x)=-\operatorname {csch} \,x\,\!}
Látható, hogy a ch x és sch x páros , a többi páratlan függvény .
sh
(
z
)
=
sh
(
z
+
2
π
i
)
és
ch
(
z
)
=
ch
(
z
+
2
π
i
)
{\displaystyle \operatorname {sh} (z)=\operatorname {sh} (z+2\pi i)\quad {\text{ és }}\quad \operatorname {ch} (z)=\operatorname {ch} (z+2\pi i)}
így a többi hiperbolikus függvény is periodikus
2
π
i
{\displaystyle 2\pi i}
sh
(
z
1
±
z
2
)
=
sh
(
z
1
)
⋅
ch
(
z
2
)
±
sh
(
z
2
)
⋅
ch
(
z
1
)
{\displaystyle \operatorname {sh} (z_{1}\pm z_{2})=\operatorname {sh} (z_{1})\cdot \operatorname {ch} (z_{2})\pm \operatorname {sh} (z_{2})\cdot \operatorname {ch} (z_{1})}
ch
(
z
1
±
z
2
)
=
ch
(
z
1
)
⋅
ch
(
z
2
)
±
sh
(
z
1
)
⋅
sh
(
z
2
)
{\displaystyle \operatorname {ch} (z_{1}\pm z_{2})=\operatorname {ch} (z_{1})\cdot \operatorname {ch} (z_{2})\pm \operatorname {sh} (z_{1})\cdot \operatorname {sh} (z_{2})}
th
(
z
1
±
z
2
)
=
th
(
z
1
)
±
th
(
z
2
)
1
±
th
(
z
1
)
th
(
z
2
)
{\displaystyle \operatorname {th} (z_{1}\pm z_{2})={\frac {\operatorname {th} (z_{1})\pm \operatorname {th} (z_{2})}{1\pm \operatorname {th} (z_{1})\operatorname {th} (z_{2})}}}
th
(
α
+
β
)
=
th
α
+
th
β
1
+
th
α
th
β
{\displaystyle \operatorname {th} (\alpha +\beta )={\frac {\operatorname {th} \alpha +\operatorname {th} \beta }{1+\operatorname {th} \alpha \,\operatorname {th} \beta }}}
cth
(
α
+
β
)
=
1
+
cth
α
cth
β
cth
α
+
cth
β
{\displaystyle \operatorname {cth} (\alpha +\beta )={\frac {1+\operatorname {cth} \alpha \,\operatorname {cth} \beta }{\operatorname {cth} \alpha +\operatorname {cth} \beta }}}
Speciálisan, ha
y
:=
x
{\displaystyle y:=x}
sh
2
x
=
2
⋅
sh
x
ch
x
ch
2
x
=
ch
2
x
+
sh
2
x
=
2
⋅
ch
2
x
−
1
=
2
⋅
sh
2
x
+
1
{\displaystyle {\begin{aligned}\operatorname {sh} 2x&=2\cdot \operatorname {sh} x\operatorname {ch} x\ \\\operatorname {ch} 2x&=\operatorname {ch} ^{2}x+\operatorname {sh} ^{2}x=2\cdot \operatorname {ch} ^{2}x-1=2\cdot \operatorname {sh} ^{2}x+1\end{aligned}}}
illetve, ha
y
:=
2
x
{\displaystyle y:=2x}
sh
3
x
=
4
⋅
sh
3
x
+
3
sh
x
ch
3
x
=
4
⋅
ch
3
x
−
3
ch
x
{\displaystyle {\begin{aligned}\operatorname {sh} 3x&=4\cdot \operatorname {sh} ^{3}x+3\operatorname {sh} x\ \\\operatorname {ch} 3x&=4\cdot \operatorname {ch} ^{3}x-3\operatorname {ch} x\end{aligned}}}
Összegzés:
sh
x
±
sh
y
=
2
sh
x
±
y
2
ch
x
∓
y
2
ch
x
+
ch
y
=
2
ch
x
+
y
2
ch
x
−
y
2
ch
x
−
ch
y
=
2
sh
x
+
y
2
sh
x
−
y
2
{\displaystyle {\begin{aligned}\operatorname {sh} x\pm \operatorname {sh} y&=2\operatorname {sh} {\frac {x\pm y}{2}}\operatorname {ch} {\frac {x\mp y}{2}}\\\operatorname {ch} x+\operatorname {ch} y&=2\operatorname {ch} {\frac {x+y}{2}}\operatorname {ch} {\frac {x-y}{2}}\\\operatorname {ch} x-\operatorname {ch} y&=2\operatorname {sh} {\frac {x+y}{2}}\operatorname {sh} {\frac {x-y}{2}}\end{aligned}}}
sh
2
x
=
1
2
(
ch
(
2
x
)
−
1
)
ch
2
x
=
1
2
(
ch
(
2
x
)
+
1
)
{\displaystyle {\begin{aligned}\operatorname {sh} ^{2}x={\frac {1}{2}}{\Big (}\operatorname {ch} (2x)-1{\Big )}\\\operatorname {ch} ^{2}x={\frac {1}{2}}{\Big (}\operatorname {ch} (2x)+1{\Big )}\end{aligned}}}
ch
2
(
z
)
−
sh
2
(
z
)
=
1
{\displaystyle {\operatorname {ch} }^{2}(z)-{\operatorname {sh} }^{2}(z)=1}
ch
z
+
sh
z
=
e
z
{\displaystyle \operatorname {ch} z+\operatorname {sh} z\ =e^{z}}
ch
z
−
sh
z
=
e
−
z
{\displaystyle \operatorname {ch} z-\operatorname {sh} z\ =e^{-z}}
sh
(
ln
φ
)
=
1
2
{\displaystyle \operatorname {sh} (\ln \varphi )={\tfrac {1}{2}}}
φ
{\displaystyle \varphi }
aranymetszés .A hiperbolikus kotangensnek két fixpontja van, azaz két hely, ami megegyezik az ott felvett értékkel:
cth
u
=
u
{\displaystyle \operatorname {cth} \,u=u}
u
±
=
±
1,199
67864
…
{\displaystyle u_{\pm }=\pm 1{,}19967864\dots }
A085984 sorozat az OEIS -ben))Ha
x
,
y
∈
R
{\displaystyle x,y\in \mathbb {R} }
sh
(
x
+
i
y
)
=
cos
y
sh
x
+
i
sin
y
ch
x
ch
(
x
+
i
y
)
=
cos
y
ch
x
+
i
sin
y
sh
x
sin
(
x
+
i
y
)
=
sin
x
ch
y
+
i
cos
x
sh
y
cos
(
x
+
i
y
)
=
cos
x
ch
y
−
i
sin
x
sh
y
{\displaystyle {\begin{aligned}\operatorname {sh} (x+i\,y)&=\cos y\,\operatorname {sh} x+i\sin y\,\operatorname {ch} x\\\operatorname {ch} (x+i\,y)&=\cos y\,\operatorname {ch} x+i\sin y\,\operatorname {sh} x\\\sin(x+i\,y)&=\sin x\,\operatorname {ch} y+i\cos x\,\operatorname {sh} y\\\cos(x+i\,y)&=\cos x\,\operatorname {ch} y-i\sin x\,\operatorname {sh} y\\\end{aligned}}}
Például a harmadik és a negyedik egyenlőség levezethető a következőképpen:
Ha
z
=
x
+
i
y
{\displaystyle z=x+i\,y}
exp
(
i
z
)
=
cos
(
x
+
i
y
)
+
i
sin
(
x
+
i
y
)
=
exp
(
i
(
x
+
i
y
)
)
=
exp
(
i
x
)
exp
(
i
(
i
y
)
)
=
(
cos
x
cos
(
i
y
)
−
sin
x
sin
(
i
y
)
)
+
i
(
cos
x
sin
(
i
y
)
+
sin
x
cos
(
i
y
)
)
=
(
cos
x
ch
y
−
i
sin
x
sh
y
)
+
i
(
sin
x
ch
y
+
i
cos
x
sh
y
)
{\displaystyle {\begin{aligned}\exp(iz)&=\cos(x+i\,y)+i\sin(x+i\,y)\\&=\exp(i\,(x+i\,y))\\&=\exp(i\,x)\,\exp(i\,(i\,y))\\&=(\cos x\,\cos(i\,y)-\sin x\,\sin(i\,y))+i\,(\cos x\,\sin(i\,y)+\sin x\,\cos(i\,y))\\&=(\cos x\,\operatorname {ch} y-i\sin x\,\operatorname {sh} y)+i\,(\sin x\,\operatorname {ch} y+i\cos x\,\operatorname {sh} y)\\\end{aligned}}}
Az együtthatók összehasonlításával:
cos
(
x
+
i
y
)
=
cos
x
ch
y
−
i
sin
x
sh
y
sin
(
x
+
i
y
)
=
sin
x
ch
y
+
i
cos
x
sh
y
{\displaystyle {\begin{aligned}\cos(x+i\,y)&=\cos x\,\operatorname {ch} y-i\sin x\,\operatorname {sh} y\\\sin(x+i\,y)&=\sin x\,\operatorname {ch} y+i\cos x\,\operatorname {sh} y\\\end{aligned}}}
th
(
x
+
i
y
)
=
sh
(
2
x
)
ch
(
2
x
)
+
cos
(
2
y
)
+
i
sin
(
2
y
)
ch
(
2
x
)
+
cos
(
2
y
)
{\displaystyle \operatorname {th} (x+i\,y)={\frac {\operatorname {sh} (2x)}{\operatorname {ch} (2x)+\cos(2y)}}+i\,{\frac {\sin(2y)}{\operatorname {ch} (2x)+\cos(2y)}}}
th
(
i
y
)
=
i
th
y
{\displaystyle \operatorname {th} (i\,y)=i\,\operatorname {th} y}
cth
(
x
+
i
y
)
=
sh
(
2
x
)
ch
(
2
x
)
−
cos
(
2
y
)
+
i
−
sin
(
2
y
)
ch
(
2
x
)
−
cos
(
2
y
)
{\displaystyle \operatorname {cth} (x+i\,y)={\frac {\operatorname {sh} (2x)}{\operatorname {ch} (2x)-\cos(2y)}}+i\,{\frac {-\sin(2y)}{\operatorname {ch} (2x)-\cos(2y)}}}
cth
(
i
y
)
=
−
i
ctg
y
{\displaystyle \operatorname {cth} (i\,y)=-i\,\operatorname {ctg} y}
sech
(
x
+
i
y
)
=
2
cosh
(
x
)
cos
(
y
)
cosh
(
2
x
)
+
cos
(
2
y
)
+
i
−
2
sinh
(
x
)
sin
(
y
)
cosh
(
2
x
)
+
cos
(
2
y
)
sech
(
i
y
)
=
sec
(
y
)
csch
(
x
+
i
y
)
=
2
sinh
(
x
)
cos
(
y
)
cosh
(
2
x
)
−
cos
(
2
y
)
+
i
−
2
cosh
(
x
)
sin
(
y
)
cosh
(
2
x
)
−
cos
(
2
y
)
csch
(
i
y
)
=
−
i
csc
(
y
)
{\displaystyle {\begin{aligned}&\operatorname {sech} (x+\mathrm {i} y)={\frac {2\cosh(x)\cos(y)}{\cosh(2x)+\cos(2y)}}+\mathrm {i} {\frac {-2\sinh(x)\sin(y)}{\cosh(2x)+\cos(2y)}}\\&\operatorname {sech} (\mathrm {i} y)=\sec(y)\\&\operatorname {csch} (x+\mathrm {i} y)={\frac {2\sinh(x)\cos(y)}{\cosh(2x)-\cos(2y)}}+\mathrm {i} \;{\frac {-2\cosh(x)\sin(y)}{\cosh(2x)-\cos(2y)}}\\&\operatorname {csch} (\mathrm {i} y)=-\mathrm {i} \csc(y)\end{aligned}}}
A szögfüggvények és a hiperbolikus függvények közötti kapcsolat:
sh
(
x
)
=
tg
(
gd
x
)
=
tg
(
φ
)
(3)
ch
(
x
)
=
sec
(
gd
x
)
=
sec
(
φ
)
th
(
x
)
=
sin
(
gd
x
)
=
sin
(
φ
)
(4)
sech
(
x
)
=
cos
(
gd
x
)
=
cos
(
φ
)
csch
(
x
)
=
ctg
(
gd
x
)
=
ctg
(
φ
)
cth
(
x
)
=
csc
(
gd
x
)
=
csc
(
φ
)
{\displaystyle {\begin{aligned}\operatorname {sh} (x)&=\operatorname {tg} (\operatorname {gd} \,x)&=&\operatorname {tg} (\varphi )&\quad &{\text{(3)}}\\\operatorname {ch} (x)&=\sec(\operatorname {gd} \,x)&=&\sec(\varphi )\\\operatorname {th} (x)&=\sin(\operatorname {gd} \,x)&=&\sin(\varphi )&\quad &{\text{(4)}}\\\operatorname {sech} (x)&=\cos(\operatorname {gd} \,x)&=&\cos(\varphi )\\\operatorname {csch} (x)&=\operatorname {ctg} (\operatorname {gd} \,x)&=&\operatorname {ctg} (\varphi )\\\operatorname {cth} (x)&=\csc(\operatorname {gd} \,x)&=&\csc(\varphi )\\\end{aligned}}}
ahol
gd
{\displaystyle \operatorname {gd} }
Gudermann-függvény .
Függvény
sh
{\displaystyle \operatorname {sh} }
ch
{\displaystyle \operatorname {ch} }
th
{\displaystyle \operatorname {th} }
cth
{\displaystyle \operatorname {cth} }
sech
{\displaystyle \operatorname {sech} }
csch
{\displaystyle \operatorname {csch} }
sh
(
x
)
=
{\displaystyle \operatorname {sh} (x)=}
sh
(
x
)
{\displaystyle \operatorname {sh} (x)\,}
sgn
(
x
)
ch
2
(
x
)
−
1
{\displaystyle \operatorname {sgn}(x){\sqrt {\operatorname {ch} ^{2}(x)-1}}}
th
(
x
)
1
−
th
2
(
x
)
{\displaystyle {\frac {\operatorname {th} (x)}{\sqrt {1-\operatorname {th} ^{2}(x)}}}}
sgn
(
x
)
cth
2
(
x
)
−
1
{\displaystyle {\frac {\operatorname {sgn}(x)}{\sqrt {\operatorname {cth} ^{2}(x)-1}}}}
sgn
(
x
)
1
−
sech
2
(
x
)
sech
(
x
)
{\displaystyle \operatorname {sgn}(x){\frac {\sqrt {1-\operatorname {sech} ^{2}(x)}}{\operatorname {sech} (x)}}}
1
csch
(
x
)
{\displaystyle {\frac {1}{\operatorname {csch} (x)}}}
ch
(
x
)
=
{\displaystyle \operatorname {ch} (x)=}
1
+
sh
2
(
x
)
{\displaystyle \,{\sqrt {1+\operatorname {sh} ^{2}(x)}}}
ch
(
x
)
{\displaystyle \,\operatorname {ch} (x)}
1
1
−
th
2
(
x
)
{\displaystyle \,{\frac {1}{\sqrt {1-\operatorname {th} ^{2}(x)}}}}
|
cth
|
cth
2
(
x
)
−
1
{\displaystyle \,{\frac {\left|\operatorname {cth} \right|}{\sqrt {\operatorname {cth} ^{2}(x)-1}}}}
1
sech
(
x
)
{\displaystyle \,{\frac {1}{\operatorname {sech} (x)}}}
1
+
csch
2
(
x
)
|
csch
(
x
)
|
{\displaystyle \,{\frac {\sqrt {1+\operatorname {csch} ^{2}(x)}}{\left|\operatorname {csch} (x)\right|}}}
th
(
x
)
=
{\displaystyle \operatorname {th} (x)=}
sh
(
x
)
1
+
sh
2
(
x
)
{\displaystyle \,{\frac {\operatorname {sh} (x)}{\sqrt {1+\operatorname {sh} ^{2}(x)}}}}
sgn
(
x
)
ch
2
(
x
)
−
1
ch
(
x
)
{\displaystyle \,\operatorname {sgn}(x){\frac {\sqrt {\operatorname {ch} ^{2}(x)-1}}{\operatorname {ch} (x)}}}
th
(
x
)
{\displaystyle \,\operatorname {th} (x)}
1
cth
(
x
)
{\displaystyle \,{\frac {1}{\operatorname {cth} (x)}}}
sgn
(
x
)
1
−
sech
2
(
x
)
{\displaystyle \,\operatorname {sgn}(x){\sqrt {1-\operatorname {sech} ^{2}(x)}}}
sgn
(
x
)
1
+
csch
2
(
x
)
{\displaystyle \,{\frac {\operatorname {sgn}(x)}{\sqrt {1+\operatorname {csch} ^{2}(x)}}}}
cth
(
x
)
=
{\displaystyle \operatorname {cth} (x)=}
1
+
sh
2
(
x
)
sh
(
x
)
{\displaystyle \,{\frac {\sqrt {1+\operatorname {sh} ^{2}(x)}}{\operatorname {sh} (x)}}}
sgn
(
x
)
ch
(
x
)
ch
2
(
x
)
−
1
{\displaystyle \,\operatorname {sgn}(x){\frac {\operatorname {ch} (x)}{\sqrt {\operatorname {ch} ^{2}(x)-1}}}}
1
th
(
x
)
{\displaystyle \,{\frac {1}{\operatorname {th} (x)}}}
cth
(
x
)
{\displaystyle \,\operatorname {cth} (x)}
sgn
(
x
)
1
−
sech
2
(
x
)
{\displaystyle \,{\frac {\operatorname {sgn}(x)}{\sqrt {1-\operatorname {sech} ^{2}(x)}}}}
sgn
(
x
)
1
+
csch
2
(
x
)
{\displaystyle \,\operatorname {sgn}(x){\sqrt {1+\operatorname {csch} ^{2}(x)}}}
sech
(
x
)
=
{\displaystyle \operatorname {sech} (x)=}
1
1
+
sh
2
(
x
)
{\displaystyle \,{\frac {1}{\sqrt {1+\operatorname {sh} ^{2}(x)}}}}
1
ch
(
x
)
{\displaystyle \,{\frac {1}{\operatorname {ch} (x)}}}
1
−
th
2
(
x
)
{\displaystyle \,{\sqrt {1-\operatorname {th} ^{2}(x)}}}
cth
2
(
x
)
−
1
|
cth
(
x
)
|
{\displaystyle \,{\frac {\sqrt {\operatorname {cth} ^{2}(x)-1}}{\left|\operatorname {cth} (x)\right|}}}
sech
(
x
)
{\displaystyle \,\operatorname {sech} (x)}
|
csch
(
x
)
|
1
+
csch
2
(
x
)
{\displaystyle \,{\frac {\left|\operatorname {csch} (x)\right|}{\sqrt {1+\operatorname {csch} ^{2}(x)}}}}
csch
(
x
)
=
{\displaystyle \operatorname {csch} (x)=}
1
sh
(
x
)
{\displaystyle \,{\frac {1}{\operatorname {sh} (x)}}}
sgn
(
x
)
ch
2
(
x
)
−
1
{\displaystyle \,{\frac {\operatorname {sgn}(x)}{\sqrt {\operatorname {ch} ^{2}(x)-1}}}}
1
−
th
2
(
x
)
th
(
x
)
{\displaystyle \,{\frac {\sqrt {1-\operatorname {th} ^{2}(x)}}{\operatorname {th} (x)}}}
sgn
(
x
)
cth
2
(
x
)
−
1
{\displaystyle \,\operatorname {sgn}(x){\sqrt {\operatorname {cth} ^{2}(x)-1}}}
sgn
(
x
)
sech
(
x
)
1
−
sech
2
(
x
)
{\displaystyle \,\operatorname {sgn}(x){\frac {\operatorname {sech} (x)}{\sqrt {1-\operatorname {sech} ^{2}(x)}}}}
csch
(
x
)
{\displaystyle \,\operatorname {csch} (x)}
d
d
x
sh
x
=
ch
x
{\displaystyle {\frac {d}{dx}}\operatorname {sh} x=\operatorname {ch} x\,}
d
d
x
ch
x
=
sh
x
{\displaystyle {\frac {d}{dx}}\operatorname {ch} x=\operatorname {sh} x\,}
d
d
x
th
x
=
1
−
th
2
x
=
sch
2
x
=
1
/
ch
2
x
{\displaystyle {\frac {d}{dx}}\operatorname {th} x=1-\operatorname {th} ^{2}x={\hbox{sch}}^{2}x=1/\operatorname {ch} ^{2}x\,}
d
d
x
cth
x
=
1
−
cth
2
x
=
−
csch
2
x
=
−
1
/
sh
2
x
{\displaystyle {\frac {d}{dx}}\operatorname {cth} x=1-\operatorname {cth} ^{2}x=-{\hbox{csch}}^{2}x=-1/\operatorname {sh} ^{2}x\,}
d
d
x
csch
x
=
−
csch
x
cth
x
{\displaystyle {\frac {d}{dx}}\ {\hbox{csch}}x=-{\hbox{csch}}\ x\operatorname {cth} x\,}
d
d
x
sech
x
=
−
sech
x
th
x
{\displaystyle {\frac {d}{dx}}\ {\hbox{sech}}x=-{\hbox{sech}}\ x\operatorname {th} x\,}
A tangens hiperbolicus
n
{\displaystyle n}
d
n
d
z
n
th
z
=
2
n
+
1
e
2
z
(
1
+
e
2
z
)
n
+
1
∑
k
=
0
n
−
1
(
−
1
)
k
A
n
,
k
e
2
k
z
{\displaystyle {\frac {\mathrm {d} ^{n}}{\mathrm {d} z^{n}}}\operatorname {th} z={\frac {2^{n+1}\mathrm {e} ^{2z}}{(1+\mathrm {e} ^{2z})^{n+1}}}\sum _{k=0}^{n-1}(-1)^{k}A_{n,k}\,\mathrm {e} ^{2kz}}
ahol An,k Euler-számok .
d
d
x
sech
x
=
−
sech
x
⋅
th
x
=
−
sh
x
ch
2
x
d
d
x
csch
x
=
−
csch
x
⋅
cth
x
=
−
ch
x
sh
2
x
=
−
csch
x
⋅
1
+
csch
2
x
{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {sech} \ x&=-\operatorname {sech} \ x\cdot \operatorname {th} \ x=-{\frac {\operatorname {sh} x}{\operatorname {ch} ^{2}x}}\\{\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {csch} \ x&=-\operatorname {csch} \ x\cdot \operatorname {cth} \ x=-{\frac {\operatorname {ch} x}{\operatorname {sh} ^{2}x}}=-\operatorname {csch} \ x\cdot {\sqrt {1+\operatorname {csch} ^{2}x}}\\\end{aligned}}}
∫
sh
c
x
d
x
=
1
c
ch
c
x
+
C
{\displaystyle \int \operatorname {sh} cx\,dx={\frac {1}{c}}\operatorname {ch} cx+C}
∫
ch
c
x
d
x
=
1
c
sh
c
x
+
C
{\displaystyle \int \operatorname {ch} cx\,dx={\frac {1}{c}}\operatorname {sh} cx+C}
∫
th
c
x
d
x
=
1
c
ln
|
ch
c
x
|
+
C
{\displaystyle \int \operatorname {th} cx\,dx={\frac {1}{c}}\ln |\operatorname {ch} cx|+C}
∫
cth
c
x
d
x
=
1
c
ln
|
sh
c
x
|
+
C
{\displaystyle \int \operatorname {cth} cx\,dx={\frac {1}{c}}\ln |\operatorname {sh} cx|+C}
∫
sech
x
d
x
=
arctg
(
sh
x
)
+
C
∫
csch
x
d
x
=
ln
|
th
x
2
|
+
C
{\displaystyle {\begin{aligned}\int \operatorname {sech} x\ \mathrm {d} x&=\operatorname {arctg} \left(\operatorname {sh} x\right)+C\\\int \operatorname {csch} x\ \mathrm {d} x&=\ln \left|\operatorname {th} \,{\frac {x}{2}}\right|+C\end{aligned}}}
A fenti kifejezésekben C az integrálás állandója.
Improprius integrál:
∫
−
∞
∞
d
x
ch
x
=
π
.
{\displaystyle \int \limits _{-\infty }^{\infty }{\frac {\mathrm {d} x}{\operatorname {ch} x}}=\pi .}
A
sh
{\displaystyle \operatorname {sh} }
ch
{\displaystyle \operatorname {ch} }
d
2
d
z
2
f
(
z
)
=
f
(
z
)
{\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} z^{2}}}f(z)=f(z)}
lineáris differenciálegyenlet alaprendszerét , más néven megoldásbázisát alkotják, ugyanúgy mint az
e
z
{\displaystyle e^{z}}
e
−
z
{\displaystyle e^{-z}}
f
i
(
z
)
{\displaystyle f_{i}(z)}
f
1
(
0
)
=
0
{\displaystyle f_{1}(0)=0}
f
1
′
(
0
)
=
1
{\displaystyle f_{1}'(0)=1}
f
2
(
0
)
=
1
{\displaystyle f_{2}(0)=1}
f
2
′
(
0
)
=
0
{\displaystyle f_{2}'(0)=0}
sh
{\displaystyle \operatorname {sh} }
ch
{\displaystyle \operatorname {ch} }
A
th
{\displaystyle \operatorname {th} }
f
′
=
1
−
f
2
{\displaystyle f^{\prime }=1-f^{2}}
1
2
f
′
′
=
f
3
−
f
=
f
(
f
2
−
1
)
{\displaystyle {\frac {1}{2}}f^{\prime \prime }=f^{3}-f=f(f^{2}-1)}
az
f
(
0
)
=
0
{\displaystyle f(0)=0}
f
′
(
∞
)
=
0
{\displaystyle f^{\prime }(\infty )=0}
A hiperbolikus függvények Taylor-sorai :
sh
x
=
x
+
x
3
3
!
+
x
5
5
!
+
x
7
7
!
+
⋯
=
∑
n
=
0
∞
x
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle \operatorname {sh} x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}}
ch
x
=
1
+
x
2
2
!
+
x
4
4
!
+
x
6
6
!
+
⋯
=
∑
n
=
0
∞
x
2
n
(
2
n
)
!
{\displaystyle \operatorname {ch} x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}}
th
x
=
x
−
x
3
3
+
2
x
5
15
−
17
x
7
315
+
⋯
=
∑
n
=
1
∞
2
2
n
(
2
2
n
−
1
)
B
2
n
x
2
n
−
1
(
2
n
)
!
,
|
x
|
<
π
2
{\displaystyle \operatorname {th} x=x-{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}-{\frac {17x^{7}}{315}}+\cdots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}
cth
x
=
1
x
+
x
3
−
x
3
45
+
2
x
5
945
+
⋯
=
1
x
+
∑
n
=
1
∞
2
2
n
B
2
n
x
2
n
−
1
(
2
n
)
!
,
0
<
|
x
|
<
π
{\displaystyle \operatorname {cth} x={\frac {1}{x}}+{\frac {x}{3}}-{\frac {x^{3}}{45}}+{\frac {2x^{5}}{945}}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }
Laurent-sor )
sch
x
=
1
−
x
2
2
+
5
x
4
24
−
61
x
6
720
+
⋯
=
∑
n
=
0
∞
E
2
n
x
2
n
(
2
n
)
!
,
|
x
|
<
π
2
{\displaystyle \operatorname {sch} \,x=1-{\frac {x^{2}}{2}}+{\frac {5x^{4}}{24}}-{\frac {61x^{6}}{720}}+\cdots =\sum _{n=0}^{\infty }{\frac {E_{2n}x^{2n}}{(2n)!}},\left|x\right|<{\frac {\pi }{2}}}
csch
x
=
1
x
−
x
6
+
7
x
3
360
−
31
x
5
15120
+
⋯
=
1
x
+
∑
n
=
1
∞
2
(
1
−
2
2
n
−
1
)
B
2
n
x
2
n
−
1
(
2
n
)
!
,
0
<
|
x
|
<
π
{\displaystyle \operatorname {csch} \,x={\frac {1}{x}}-{\frac {x}{6}}+{\frac {7x^{3}}{360}}-{\frac {31x^{5}}{15120}}+\cdots ={\frac {1}{x}}+\sum _{n=1}^{\infty }{\frac {2(1-2^{2n-1})B_{2n}x^{2n-1}}{(2n)!}},0<\left|x\right|<\pi }
Laurent-sor )ahol
B
n
{\displaystyle B_{n}\,}
Bernoulli-szám
E
n
{\displaystyle E_{n}\,}
th
x
=
sgn
x
[
1
+
∑
k
=
1
∞
(
−
1
)
k
2
e
−
2
k
|
x
|
]
{\displaystyle \operatorname {th} x=\operatorname {sgn} x\left[1+\sum \limits _{k=1}^{\infty }(-1)^{k}\,2\,\mathrm {e} ^{-2k|x|}\right]}
cth
x
=
1
x
+
∑
k
=
1
∞
2
x
k
2
π
2
+
x
2
{\displaystyle \operatorname {cth} x={\frac {1}{x}}+\sum \limits _{k=1}^{\infty }{\frac {2x}{k^{2}\pi ^{2}+x^{2}}}}
A tangens hyperbolicus Taylor-sora így kezdődik:
th
x
=
∑
n
=
1
∞
(
−
1
)
n
−
1
⋅
2
2
n
(
2
2
n
−
1
)
(
2
n
)
!
⋅
B
2
n
⋅
x
2
n
−
1
=
x
−
1
3
x
3
+
2
15
x
5
+
⋯
{\displaystyle \operatorname {th} x=\sum \limits _{n=1}^{\infty }(-1)^{n-1}\cdot {\frac {2^{2n}(2^{2n}-1)}{(2n)!}}\cdot B_{2n}\cdot x^{2n-1}=x-{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+\cdots }
ahol
B
n
{\displaystyle B_{n}\,}
Bernoulli-szám . A konvergenciasugár
π
/
2
{\displaystyle \pi /2}
Legyen
n
∈
N
{\displaystyle n\in \mathbb {N} }
z
{\displaystyle z}
sh
z
=
(
2
i
)
n
−
1
∏
k
=
0
n
−
1
sh
z
+
k
π
i
n
ch
z
=
2
n
−
1
∏
k
=
0
n
−
1
ch
z
+
(
k
−
n
−
1
2
)
π
i
n
{\displaystyle {\begin{aligned}&\operatorname {sh} z={\left({\frac {2}{i}}\right)}^{\!\!n-1}\,\prod \limits _{k=0}^{n-1}\operatorname {sh} {\frac {z+k\,\pi \,i}{n}}\\&\operatorname {ch} z=2^{n-1}\prod \limits _{k=0}^{n-1}\operatorname {ch} {\frac {z+\left(k-{\frac {n-1}{2}}\right)\,\pi \,i}{n}}\end{aligned}}}
sh
x
=
x
⋅
∏
k
=
1
∞
(
1
+
x
2
(
k
π
)
2
)
ch
x
=
∏
k
=
1
∞
(
1
+
4
x
2
(
2
k
−
1
)
2
π
2
)
{\displaystyle {\begin{aligned}&\operatorname {sh} x=x\cdot \prod _{k=1}^{\infty }\left(1+{\frac {x^{2}}{(k\pi )^{2}}}\right)\\&\operatorname {ch} x=\prod _{k=1}^{\infty }\left(1+{\frac {4x^{2}}{(2k-1)^{2}\pi ^{2}}}\right)\end{aligned}}}
Johann Heinrich Lambert képlete:
th
x
=
x
1
+
x
2
3
+
x
2
5
+
…
{\displaystyle \operatorname {th} x={\frac {x}{1+{\cfrac {x^{2}}{3+{\cfrac {x^{2}}{5+\ldots }}}}}}}
Definiáljuk a következő halmazokat a komplex számokon:
A
:=
{
z
∈
C
∣
−
π
/
2
<
Im
z
<
π
/
2
}
{\displaystyle A:=\{z\in \mathbb {C} \mid -\pi /2<\operatorname {Im} \,z<\pi /2\}}
B
:=
{
z
∈
C
∣
Re
z
≠
0
∨
|
Im
z
|
<
1
}
{\displaystyle B:=\{z\in \mathbb {C} \mid \operatorname {Re} \,z\neq 0\vee |\operatorname {Im} \,z|<1\}}
Ekkor az
sh
x
{\displaystyle \operatorname {sh} x}
A
{\displaystyle A}
B
{\displaystyle B}
Definiáljuk a következő halmazokat a komplex számokon:
A
:=
{
z
∈
C
∣
0
<
Im
z
<
π
}
{\displaystyle A:=\{z\in \mathbb {C} \mid 0<\operatorname {Im} \,z<\pi \}}
B
:=
{
z
∈
C
∣
Im
z
≠
0
∨
|
Re
z
|
<
1
}
{\displaystyle B:=\{z\in \mathbb {C} \mid \operatorname {Im} \,z\neq 0\vee |\operatorname {Re} \,z|<1\}}
Ekkor az
ch
x
{\displaystyle \operatorname {ch} x}
A
{\displaystyle A}
B
{\displaystyle B}
A hiperbolikus függvények inverz függvényeit áreafüggvényeknek vagy inverz hiperbolikus függvényeknek nevezzük:
áreaszinusz hiperbolikus és áreakoszinusz hiperbolikus
áreatangens hiperbolikus és áreakotangens hiperbolikus
áreaszekáns hiperbolikus és áreakoszekáns hiperbolikus Az inverz függvényeket csak olyan leszűkítéseken lehet definiálni, ahol az adott függvény egyértelmű. Így a szinusz hiperbolikust nem kell leszűkíteni, de például a koszinusz hiperbolikust igen: a koszinusz hipőerbolikust az
[
0
,
+
∞
[
{\displaystyle [0,+\infty [}
arsinh
x
=
ln
(
x
+
x
2
+
1
)
{\displaystyle \operatorname {arsinh} x=\ln \left(x+{\sqrt {x^{2}+1}}\right)\ }
arcosh
x
=
ln
(
x
+
x
2
−
1
)
{\displaystyle \operatorname {arcosh} x=\ln \left(x+{\sqrt {x^{2}-1}}\right)\ }
A tangens hiperbolicus bijektív
th
:
R
→
(
−
1
,
1
)
{\displaystyle \operatorname {th} \colon \mathbb {R} \rightarrow (-1,1)}
(
−
1
,
1
)
{\displaystyle (-1,1)}
artanh
x
=
1
2
ln
1
+
x
1
−
x
.
{\displaystyle \operatorname {artanh} x={\frac {1}{2}}\ln {\frac {1+x}{1-x}}.}
Az area cotangens hiperbolicus:
arcoth
x
=
1
2
ln
x
+
1
x
−
1
{\displaystyle \operatorname {arcoth} x={\frac {1}{2}}\ln {\frac {x+1}{x-1}}}
a
(
−
1
,
1
)
{\displaystyle (-1,1)}
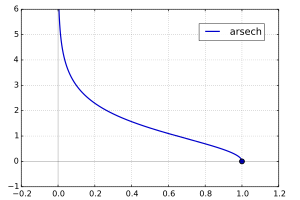
Az áreafüggvények grafikonja
áreaszinusz hiperbolikus
áreakoszinusz hiperbolikus
áreatangens hiperbolikus
áreakotangens hiperbolikus
áreaszekáns hiperbolikus
áreakoszekáns hiperbolikus
Kör és hiperbola kapcsolata Az x y = 1 hiperbola x > 1 tartományban lévő tetszőleges pontja hiperbolikus háromszöget határoz meg, amelyben a hiperbolikus szög melletti oldal a ch értékkel egyenlő, míg a szöggel szemben fekvő oldal az sh-val. Azonban mivel a hiperbola (1,1) pontja az origótól √2 távolságra van, ezért az oldalak hosszát 1/√2 tényezővel kell szoroznunk, hogy a helyes eredményt kapjuk.
Mint ahogy a (cos x , sin x ) pontok egy kört ( x2 + y2 = 1) határoznak meg, a (ch x , sh x ) pontok az x ² - y ² = 1 egyenlő szárú hiperbola jobb oldali görbéjét írják le. Ez ezen a könnyen ellenőrizhető azonosságon:
ch
2
x
−
sh
2
x
=
1
{\displaystyle \operatorname {ch} ^{2}x-\operatorname {sh} ^{2}x=1\,}
és azon alapul, hogy ch x > 0 minden x -re.
A hiperbolikus függvények periodikusak
2
π
i
{\displaystyle 2\pi i}
A x paraméter nem a kör középponti szöge, mint a szögfüggvényeknél, hanem a hiperbolikus „szög”, amelynek értéke a kétszerese annak a területnek, melyet az x tengely, a hiperbola és egy, a hiperbola (ch x , sh x ) pontjából az origóba húzott egyenes határol.
A hiperbolikus függvényekre igen sok olyan azonosság érvényes, melyek hasonlóak a szögfüggvények azonosságaihoz. Az Osborne-szabály kimondja, hogy minden trigonometrikus azonosságot egy analóg hiperbolikus azonossággá lehet alakítani a következőképpen:
lecseréljük a szögfüggvényt a hiperbolikus megfelelőjével és
az sh * sh kifejezés előjelét megváltoztatjuk. Néhány példa:
sh
(
x
+
y
)
=
sh
x
ch
y
+
ch
x
sh
y
{\displaystyle \operatorname {sh} (x+y)=\operatorname {sh} x\operatorname {ch} y+\operatorname {ch} x\operatorname {sh} y\,}
ch
(
x
+
y
)
=
ch
x
ch
y
+
sh
x
sh
y
{\displaystyle \operatorname {ch} (x+y)=\operatorname {ch} x\operatorname {ch} y+\operatorname {sh} x\operatorname {sh} y\,}
th
(
x
+
y
)
=
th
x
+
th
y
1
+
th
x
th
y
{\displaystyle \operatorname {th} (x+y)={\frac {\operatorname {th} x+\operatorname {th} y}{1+\operatorname {th} x\operatorname {th} y}}\,}
A „kétszeres szög” képletek:
sh
2
x
=
2
sh
x
ch
x
{\displaystyle \operatorname {sh} 2x\ =2\operatorname {sh} x\operatorname {ch} x\,}
ch
2
x
=
ch
2
x
+
sh
2
x
=
2
ch
2
x
−
1
=
2
sh
2
x
+
1
{\displaystyle \operatorname {ch} 2x\ =\operatorname {ch} ^{2}x+\operatorname {sh} ^{2}x=2\operatorname {ch} ^{2}x-1=2\operatorname {sh} ^{2}x+1\,}
és a „fél-szög” képletek:
ch
2
x
2
=
ch
x
+
1
2
{\displaystyle \operatorname {ch} ^{2}{\frac {x}{2}}={\frac {\operatorname {ch} x+1}{2}}}
sh
2
x
2
=
ch
x
−
1
2
{\displaystyle \operatorname {sh} ^{2}{\frac {x}{2}}={\frac {\operatorname {ch} x-1}{2}}}
Az
sh
x
{\displaystyle \operatorname {sh} x}
deriváltja
ch
x
{\displaystyle \operatorname {ch} x}
ch
x
{\displaystyle \operatorname {ch} x}
sh
x
{\displaystyle \operatorname {sh} x}
A tangens hyperbolicus számítható a
th
x
=
e
2
x
−
1
e
2
x
+
1
{\displaystyle \operatorname {th} x={\frac {\mathrm {e} ^{2x}-1}{\mathrm {e} ^{2x}+1}}}
Nagy értékeknél túlcsordulás jön létre, habár az eredmény nagysága ezt nem indokolja
Kis értékek esetén vészes kiegyszerűsödés adódik, így az eredmény pontatlan lesz. Ekkor a következő közelítések alkalmazhatók:
x
{\displaystyle x}
x
>
k
⋅
ln
10
2
{\displaystyle {x}>k\cdot {\frac {\ln 10}{2}}}
th
x
=
+
1
{\displaystyle \operatorname {th} x=+1}
k
{\displaystyle k}
double esetén 16.
x
{\displaystyle x}
x
<
−
k
⋅
ln
10
2
{\displaystyle {x}<-k\cdot {\frac {\ln 10}{2}}}
k
{\displaystyle k}
k
{\displaystyle k}
th
x
=
−
1
{\displaystyle \operatorname {th} x=-1}
x
{\displaystyle x}
−
0
,
1
<
x
<
+
0
,
1
{\displaystyle -0{,}1<x<+0{,}1}
th
x
=
sh
x
e
x
−
sh
x
{\displaystyle \operatorname {th} x={\frac {\operatorname {sh} x}{\mathrm {e} ^{x}-\operatorname {sh} x}}}
ahol
sh
x
{\displaystyle \operatorname {sh} x}
sh
x
=
x
+
x
3
3
!
+
x
5
5
!
+
x
7
7
!
+
…
{\displaystyle \operatorname {sh} x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+{\frac {x^{7}}{7!}}+\dots }
A többi hely esetén marad az eredeti képlet:
th
x
=
e
2
x
−
1
e
2
x
+
1
{\displaystyle \operatorname {th} x={\frac {\mathrm {e} ^{2x}-1}{\mathrm {e} ^{2x}+1}}}
Az
f
″
(
x
)
−
f
(
x
)
=
0
{\displaystyle f''(x)-f(x)=0\ }
f
(
x
)
=
a
⋅
sh
x
+
b
⋅
ch
x
{\displaystyle f(x)=a\cdot \operatorname {sh} x+b\cdot \operatorname {ch} x}
a
,
b
∈
R
{\displaystyle a,b\in \mathbb {R} }
alakú függvények.
Egy csak saját súlya által terhelt homogén lánc alakját hiperbolikus koszinusz függvénnyel lehet leírni. Ezt az alakot láncgörbének vagy katenoidnak hívják.
Egy x irányú Lorentz-transzformáció
λ
{\displaystyle \lambda }
L
=
(
ch
λ
−
sh
λ
0
0
−
sh
λ
ch
λ
0
0
0
0
1
0
0
0
0
1
)
{\displaystyle L={\begin{pmatrix}\operatorname {ch} \lambda &-\operatorname {sh} \lambda &0&0\\-\operatorname {sh} \lambda &\operatorname {ch} \lambda &0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}}
Látható a hasonlóság a forgatómátrixszal, amivel a négydimenziós Lorentz-transzformációk és a forgatások közötti hasonlóság is felismerhető.
A hiperbolikus szinusz és koszinusz a kozmológiában is előfordul. Egy lapos univerzumban, mely lényegében csak anyagot és sötét energiát tartalmaz (és ezáltal a mi univerzumunk közelítése), a skálafaktorok növekedését leíró összefüggés:
a
(
t
)
=
(
1
−
Ω
Λ
,
0
Ω
Λ
,
0
sinh
(
t
t
c
h
)
)
2
/
3
{\displaystyle a(t)=\left({\sqrt {\frac {1-\Omega _{\Lambda ,0}}{\Omega _{\Lambda ,0}}}}\sinh \left({\frac {t}{t_{\mathrm {ch} }}}\right)\right)^{2/3}}
ahol
t
c
h
=
2
3
Ω
Λ
,
0
H
0
{\displaystyle t_{\mathrm {ch} }={\frac {2}{3{\sqrt {\Omega _{\Lambda ,0}}}H_{0}}}}
H
0
{\displaystyle H_{0}}
Ω
Λ
,
0
{\displaystyle \Omega _{\Lambda ,0}}
sötét energia sűrűségparamétere. Az anyag sűrűségparaméterének időbeli függőségénél a koszinusz hiperbolikusz bukkan fel:
Ω
M
(
t
)
=
cosh
−
2
(
t
t
c
h
)
{\displaystyle \Omega _{M}(t)=\cosh ^{-2}\left({\frac {t}{t_{\mathrm {ch} }}}\right)}
A tangens és a cotangens hyperbolicus használható arra, hogy az eltelt idő függvényében kiszámítsuk a légellenállásos esés sebességét, illetve turbulens áramlásban esik a tárgy (Newton-súrlódás). A koordináta-rendszert úgy rögzítjük, hogy a helytengely felfelé mutasson, tehát a térbeli mozgás tükörképeként. A sebesség az
v
˙
=
−
g
+
k
v
2
{\displaystyle {\dot {v}}=-g+kv^{2}}
g
{\displaystyle g}
k
{\displaystyle k}
1
/
m
{\displaystyle 1/m}
v
g
=
−
g
k
<
0
{\displaystyle v_{\mathrm {g} }=-{\sqrt {\frac {g}{k}}}<0}
t
→
∞
{\displaystyle t\to \infty }
az esés vagy hajítás kezdeti sebessége kisebb, mint a végsebesség:
v
(
t
)
=
v
g
⋅
th
(
g
k
t
+
c
)
{\displaystyle v(t)=v_{\mathrm {g} }\cdot \operatorname {th} \left({\sqrt {gk}}t+c\right)}
c
=
artanh
v
(
0
)
v
g
≥
0
{\displaystyle c=\operatorname {artanh} {\frac {v(0)}{v_{\mathrm {g} }}}\geq 0}
hajítás esetén a kezdősebesség nagyobb, mint a végsebesség:
v
(
t
)
=
v
g
⋅
cth
(
g
k
t
+
c
)
{\displaystyle v(t)=v_{\mathrm {g} }\cdot \operatorname {cth} \left({\sqrt {gk}}t+c\right)}
c
=
arcoth
v
(
0
)
v
g
>
0
{\displaystyle c=\operatorname {arcoth} {\frac {v(0)}{v_{\mathrm {g} }}}>0}
A speciális relativitáselméletben a
v
{\displaystyle v}
θ
{\displaystyle \theta }
v
=
c
⋅
th
θ
{\displaystyle v=c\cdot \operatorname {th} \theta }
c
{\displaystyle c}
A kvantummechanikában egy kétállapotú rendszert ért termikus hatást írja le: Legyen
n
{\displaystyle n}
E
{\displaystyle E}
δ
n
=
n
⋅
th
E
2
k
B
T
{\displaystyle \delta n=n\cdot \operatorname {th} {\frac {E}{2k_{\mathrm {B} }T}}}
k
B
{\displaystyle k_{\mathrm {B} }}
T
{\displaystyle T}
Paramágnes mágnesesezésének leírásához fontos a Brillouin-függvény:
B
J
(
x
)
=
1
J
[
(
J
+
1
2
)
cth
(
J
x
+
x
2
)
−
1
2
cth
x
2
]
{\displaystyle B_{J}(x)={\frac {1}{J}}\left[\left(J+{\frac {1}{2}}\right)\operatorname {cth} \left(J\,x+{\frac {x}{2}}\right)-{\frac {1}{2}}\operatorname {cth} {\frac {x}{2}}\right]}
A kozmológiában Egy lapos univerzumban, mely lényegében csak anyagot és sötét energiát tartalmaz (és ezáltal a mi univerzumunk közelítése), a Hubble-paraméter időbeli változását leíró összefüggés:
H
(
t
)
=
H
g
cth
t
t
c
h
{\displaystyle H(t)=H_{g}\operatorname {cth} {\frac {t}{t_{ch}}}}
t
c
h
=
2
3
H
g
{\displaystyle t_{ch}={\frac {2}{3H_{g}}}}
H
g
=
Ω
Λ
,
0
H
0
{\displaystyle H_{g}={\sqrt {\Omega _{\Lambda ,0}}}H_{0}}
t
→
∞
{\displaystyle t\to \infty }
H
0
{\displaystyle H_{0}}
Ω
Λ
,
0
{\displaystyle \Omega _{\Lambda ,0}}
Ω
Λ
(
t
)
=
th
2
(
t
/
t
c
h
)
{\displaystyle \Omega _{\Lambda }(t)=\operatorname {th} ^{2}(t/t_{ch})}
Ez a szócikk részben vagy egészben a Hyperbelfunktion
Ez a szócikk részben vagy egészben az Areafunktion
Ez a szócikk részben vagy egészben a Sinus hyperbolicus und Kosinus hyperbolicus
Ez a szócikk részben vagy egészben a Tangens hyperbolicus und Kotangens hyperbolicus
Ez a szócikk részben vagy egészben a Sekans hyperbolicus und Kosekans hyperbolicus 




























![{\displaystyle (-\infty ,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0241c015ef4c611c9c9aeafb395e7c4a16178405)

























































































































































![{\displaystyle \operatorname {th} x=\operatorname {sgn} x\left[1+\sum \limits _{k=1}^{\infty }(-1)^{k}\,2\,\mathrm {e} ^{-2k|x|}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d95654584ab6d1b4f69a2fdf0c961723d100461e)





































































![{\displaystyle B_{J}(x)={\frac {1}{J}}\left[\left(J+{\frac {1}{2}}\right)\operatorname {cth} \left(J\,x+{\frac {x}{2}}\right)-{\frac {1}{2}}\operatorname {cth} {\frac {x}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ead61c782100c07af4648dd87309dcf09b344de)



