Hiperbola (matematika)

Hiperbola

A matematikában hiperbolának azokat a kúpszeleteket nevezik, amelyek úgy jönnek létre, hogy a végtelen kettős kúpot (forgáskúpot) metsző sík mindkét félkúpot metszi (a síknak a kúp tengelyével bezárt szöge kisebb, mint a kúp félnyílásszöge és a metsző síkra nem illeszkedik a kúp csúcsa).

A hiperbola úgy is definiálható, hogy azon pontok halmaza, melyeknek két rögzített ponttól (fókusz- vagy gyújtópontoktól) való távolságának különbségének abszolút értéke állandó. A két definíció azonosságának bizonyítását lásd a Dandelin-gömböknél.

A hiperbola a kétdimenziós Descartes-koordináta-rendszerben az alábbiakkal is definiálható:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\,$ és $B^{2}>4AC\,$,

ahol az összes együttható (A,…,F) valós, és több, mint egy (x,y) megoldás létezik. Ekkor ezek az (x,y) megoldások adják meg (koordinátaként) a hiperbola pontjait.

Hiperbola

Konjugált hiperbolák

Definíciók

• A hiperbola a fentieken kívül úgy is definiálható, hogy azon pontok halmaza, melyeknek egy adott ponttól (egyik fókusztól) való távolsága és egy egyenestől (direktrixtől vagy vezéregyenestől) való távolsága hányadosa állandó és nagyobb 1-nél. Ez az állandó a hiperbola excentricitása.

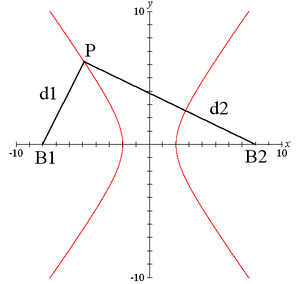
• A hiperbola másik, már említett definíciója: Azon pontok mértani helye, melyek a két fókuszponttól való távolságuk különbségének abszolút értéke állandó. Az ábra jelöléseivel:

$\left|d_{2}-d_{1}\right|=2a$.

A fókuszpontok a hiperbola egyik szimmetriatengelyén fekszenek, a köztük lévő távolság felezőpontját a hiperbola középpontjának nevezzük, a másik szimmetriatengely az elsőre a középponton átmenő merőleges egyenes.

A hiperbolának két, egymást nem metsző és nem érintő ága van. Minden határon túl növekvő távolságra fókuszoktól a hiperbola egy egyeneshez tart, melyet aszimptotának hívnak.

Konjugált hiperboláknak azokat nevezik, melyeknek aszimptotái megegyeznek, csak az aszimptoták különböző oldalain helyezkednek el.

A konjugált hiperbola speciális esete az egyenlő szárú vagy egyenlő oldalú hiperbola, melynél az aszimptoták által bezárt szög derékszög. Annak az egyenlő szárú hiperbolának az egyenlete, melynek aszimptotái a koordinátatengelyekre esnek: xy=c, ahol c állandó.

Ahogy a szinusz és koszinusz függvényekkel az ellipszis egy parametrikus egyenletrendszerét lehet felírni, a szinusz hiperbolikusz és koszinusz hiperbolikusz függvények a hiperbola parametrikus egyenletrendszerét adják.

Egyenletek

Descartes koordinátákkal

Kelet–nyugat irányban nyitott hiperbola:

${\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1$

Észak-dél irányban nyitott hiperbola

${\frac {\left(y-k\right)^{2}}{a^{2}}}-{\frac {\left(x-h\right)^{2}}{b^{2}}}=1$

Mindkét képletben (h,k) a hiperbola középpontja, a a fél-nagytengely (a két ág közötti távolság fele) és b a fél-kistengely. Megjegyezzük, hogy b lehet nagyobb, mint a.

Az excentricitás:

$e={\sqrt {1+{\frac {b^{2}}{a^{2}}}}}$

A kelet–nyugat irányban nyitott hiperbola fókuszpontjai:

$\left(h\pm c,k\right)$

és ugyanez észak-dél irányban nyitott hiperbolára:

$\left(h,k\pm c\right)$ ahol $c^{2}=a^{2}+b^{2}$

Egyenlő szárú hiperbolák egyenlete, melyek aszimptotái párhuzamosak a koordináta tengelyekkel:

$(x-h)(y-k)=c\,$

Polárkoordinátákkal

Kelet–nyugat irányban nyitott hiperbola:

$r^{2}=a\sec 2\theta \,$

Észak-dél irányban nyitott hiperbola

$r^{2}=-a\sec 2\theta \,$

Északkelet-délnyugat irányban nyitott hiperbola

$r^{2}=a\csc 2\theta \,$

Északnyugat-délkelet irányban nyitott hiperbola

$r^{2}=-a\csc 2\theta \,$

Az összes egyenletben a középpont az origóban van és a a fél-nagytengely.

Parametrikus egyenletek

Kelet–nyugat irányban nyitott hiperbola:

$x=a\sec t+h\,$ vagy $x=a\cosh t+h\,$

$y=b\tan t+k\,$ vagy $y=b\sinh t+k\,$

Észak-dél irányban nyitott hiperbola

$x=a\tan t+h\,$ vagy $x=a\sinh t+h\,$

$y=b\sec t+k\,$ vagy $y=b\cosh t+k\,$

Mindkét egyenletben (h,k) hiperbola középpontja, a a fél-nagytengely, b a fél-kistengely.

Források

• I.N. Bronstejn-K.A. Szemengyajev: Matematikai zsebkönyv 6. kiadás (Műszaki könyvkiadó, Budapest, 1987.)
• Pattantyús Gépész és villamosmérnökök kézikönyve 2. kötet (Műszaki könyvkiadó, Budapest, 1961.)

További információk

A Wikimédia Commons tartalmaz Hiperbola (matematika) témájú médiaállományokat.

• Egységhiperbola
• Kúpszelet
• Konjugált hiperbola
• Mathworld – Hiperbola

Kapcsolódó szócikkek

• Ellipszis
• Parabola
• Kör
• Dandelin-gömb

• Gábriel harsonája