Alfabetikus számírásrendszer
| Számjelölő rendszerek |
|---|
|
Arab · Babiloni · Csuvas · Egyiptomi · Görög · Inka · Maja · Római · |
| Számábrázolási rendszerek |
|
1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 · 12 · 14 · 16 · 20 · 60 |
| Vegyes alapú számrendszer |
Az alfabetikus számírásrendszer az ókorban, kora középkorban létrejött számírásrendszerek egy típusa, ahol a számjelek értékeit a fonetikus írásjelekhez – az adott írás ábécéjéhez – rendelték, majd ezeket használták a számok ábrázolására. Az alfabetikus számírásrendszerek az i. e. 6. századból a görögöktől eredeztethetők, a „ion” vagy „milétoszi” számírásból, ez vezetett a további alfabetikus rendszerek kialakulásához, melyekben a számjeleket az adott nyelv saját írásával kapcsolták össze. Széleskörű elterjedésük az i. sz. 4. és 6. századra tehető. Bár a legtöbb rendszer már kihalt, vagy legalábbis használatuk kontextusa nagymértékben lecsökkent az i. sz. 6. századra, amikor már az arab és a nyugati helyiértékes számírás váltotta fel ezeket, ugyanakkor több alfabetikus számírásrendszert még ma is használnak, de korlátozott kontextusban, mint pl. liturgikus szövegekben, listák számozására, vagy gematriára.[1]
Az alfabetikus számírásrendszereket használták egészen északon, Angliában, Germániában, Oroszországban, és egészen délen is, Etiópiában, Észak-Afrikában, Marokkótól keletre is, valamint a Közel-Keleten egészen Iránig. Története több mint kétezer éven átível, megközelítőleg az i. e. 600-tól kifejlesztett görög alfabetikus számoktól napjainkig.[2]
Struktúrája
[szerkesztés]Az alfabetikus számírásrendszerekben egy nyelv ábécéjének fonetikus írásjeleit számértékekhez rendelték, 1-9-ig, 10-90-ig, 100-tól 900-ig és így tovább, ameddig az adott nyelv betűkészlete tartott, írásukban ezzel a jelkészlettel ábrázolták a számokat is, egyszerűen rávetítették a számok decimális struktúráját az írásra.
A számszakaszok az alfabetikus rendszerekben tömörebbekké váltak, mint a korábban kialakult kumulatív-additív rendszerekben – mint pl. a római számírás -, viszont használóiknak sokkal több grafémát kellett a számíráshoz ismerniük. Viszont mivel az alfabetikus számírásrendszerek fonetikus írásjeleket használnak a számértékek ábrázolására is, ezáltal csökken a mnemonikok száma, így összességében csökkentik az írásjelek és a számjelek memorizálására fordított erőfeszítést.
Nincs egyetlen közös strukturális jellege az összes alfabetikus számírásnak. A legtöbb cifferes-additív és decimális. Kivételnek számít viszont Shirakatsi örmény számírása, mely multiplikatív-additív és részben 1000-es alapú, és a csillagászati törtek is – szexagezimális törtek -, melyek helyiértékesek és 60-as alapúak.
Elnevezésük ellenére az írások, melyekhez a kérdéses számírásrendszerek kapcsolódnak sem mindig alfabetikusak, mint a héber és a korai arab sem, melyek abdzsad vagy mássalhangzóírások, azaz elsődlegesen mássalhangzókat jelölő fonémákkal, valamint egy másik, az etióp Ge’ez írás sem igazán alfabetikus, mivel az alfaszillabikus vagy abugida jellegű írás, azaz mássalhangzót plusz magánhangzócsoportot jelölő írás.
Számjelek
[szerkesztés]A struktúrája alapján a természetes számok 1-től 900-ig történő ábrázolásához 27 jelre volt szükség, ugyanakkor nem mindegyik írás rendelkezett ennyi jellel. A görög írás kevesebbel, más írások többel. A görögök a görög ábécé 24 betűjének archaikus változatát így kiegészítették még három speciális jellel, azaz az episzemonokkal: vau, vagy digamma (6), koppa (90) és szan vagy szampi (900), hogy elérjék a teljes, 27 jelből álló jelkészletet a számok 900-ig történő ábrázolásához. A héberek a héber ábécé 22 betűjével csak 1-től 400-ig tudták a számokat jelölni – efölött additív módon ábrázolták a százasokat 900-ig. Az arab abdzsad számírásban, mivel az arab írás huszonnyolc alap mássalhangzót ismer, a fennmaradó jelet (ghayn, غ ) az 1000 numerikus értékhez rendelték. Az ősi örmény ábécé viszont harminchat betűből állt, így elegendő jelük volt nemcsak 900-ig, hanem 9000-ig is a teljes számsor ábrázolására. Az örmény íráshoz hasonlóan a grúz írás is rendelkezik annyi karakterrel, amely 9000-ig az összes számértéket ki tudja szolgálni.
Néhány alfabetikus számírásrendszer számjelei az alábbi táblázatokban láthatók:
A görög alfabetikus számírás számjelei minuszkula betűkkel:
1-esek α β γ δ ε ϛ ζ η θ 1 2 3 4 5 6 7 8 9 10-esek ι κ λ μ ν ξ ο π ϟ 10 20 30 40 50 60 70 80 90 100-asok ρ σ τ υ φ χ ψ ω ϡ 100 200 300 400 500 600 700 800 900 1000-esek ͵α ͵β ͵γ ͵δ ͵ε ͵ϛ ͵ζ ͵η ͵θ 1000 2000 3000 4000 5000 6000 7000 8000 9000
Pár szám a görög alfabetikus számírással ábrázolva:
- ͵γϡμβ = (3000 +900 + 40 + 2) = 3942
- χξϛ = (600 + 60 + 6) = 666
Összehasonlításként ugyanezek a kumulatív-additív római számírással írva:
- MMMCMXLII = (1000 + 1000 + 1000 +(1000 - 100 )+( 50- 10)+ 1+ 1) = 3942
- DCLXVI = (500 + 50 + 10+ 5+ 1) = 666
A héber alfabetikus számírás számjelei:
1-esek א ב ג ד ה ו ז ח ט 1 2 3 4 5 6 7 8 9 10-esek י כ ל מ נ ס ע פ צ 10 20 30 40 50 60 70 80 90 100-asok ק ר ש ת 100 200 300 400 1000-esek 'א 'ב 'ג 'ד 'ה 'ו 'ז 'ח 'ט 1000 2000 3000 4000 5000 6000 7000 8000 9000
Mivel a héber írás huszonkét mássalhangzó jelből áll, így csak 400-ig tudták egyedi jellel írni a számokat, az 500, 600, 700, 800, 900 értékeit az alacsonyabb százas értékek különböző additív kombinációval ábrázolták (az írás iránya jobbról balfelé tart):
- תק = (400+100) 500
- תר = (400+200) 600
- תש = (400+300) 700
- תת = (400+400) 800
- תררק = 400+200+200+100 = 900
Az örmény számírás számjelei (minuszkula betűkkel):
1-esek ա բ գ դ ե զ է ը թ 1 2 3 4 5 6 7 8 9 10-esek ժ ի լ խ ծ կ հ ձ ղ 10 20 30 40 50 60 70 80 90 100-asok ճ մ յ ն շ ո չ պ ջ 100 200 300 400 500 600 700 800 900 1000-esek ռ ս վ տ ր ց ւ փ ք 1000 2000 3000 4000 5000 6000 7000 8000 9000 10.000-esek օ ֆ 346 = յխզ
Az ősi örmény ábécé harminchat betűből állt – később még hármat adoptáltak -, így elegendő jelük volt 1000-től 9000-ig is a teljes számsor ábrázolására. Viszont a többi alfabetikus rendszertől eltérően az örmény rendszerben nincsenek a magasabb értékek ábrázolására multiplikatív számszakaszok, hanem ezeket teljesen a lexikális számokkal írták ki.
Magasabb számértékek
[szerkesztés]Ahogy az adott nyelv írásának betűkészlete véget ért, a további, magasabb számértékeket a számjelek és kiegészítő jelek multiplikatív, azaz szorzás elvű kapcsolatával jelölték. Mivel viszont a különböző írások jeleinek száma változó, így rendszerenként eltérő a magasabb értékeknél a multiplikatív struktúrára történő áttérés pontja is.
Az 1000-szeres értéket a görög, héber számírás, a szír alfabetikus számírás esetén az antikvitásban kezdetben a numerikus jel bal oldalán elhelyezett vesszővel, ill. a számjel alá helyezett vonallal jelölték.
Így pl. a görög alfabetikus számírásban:
- β = 2
- ͵β = 2.000
- ͵κ = 20.000
Egy második szintű multiplikatív módszer bevezetésével tudták még tovább bővíteni a számkört. A 10.000-szeres értékekre a görögök esetén legáltalánosabb az Arisztarkhosz által bevezetett módszer volt, egy alfabetikus számszakaszt helyeztek egy M karakter (myriades = 10.000) fölé, ezzel jelölték a szám 10.000-rel való szorzását.[3] Ezzel a módszerrel 100.000.000-ig, azaz 108-ig tudták ábrázolni a számokat.
Így pl. a 20.704-et – két myriad hétszáz négy (2 x 10.000 + 700 + 4) – a következőképp ábrázolták:
ψδ = 20.704
Pergai Apollóniosz a multiplikatív elv mellett a nagy számok ábrázolására egyedi módszert alakított ki, az M = myriades = 10.000 fölé helyezett alfabetikus számok – α -tól θ-ig, azaz 1-től 9-ig – nála a 10.000 hatványait jelölték, az M utáni számok pedig ezzel multiplikatívan kapcsolódtak.
Így a 5.462.360.064.000.000-t a következőképp tudta ábrázolni:
͵EYZB ͵ΓX ͵FY 100003 × 5462 + 100002 × 3600 + 100001 × 6400
Mivel nem mindegyik alfabetikus számírásrendszert alkalmazták matematikai, csillagászati munkákban, ahol a magas számértékek ábrázolása feltétlenül szükséges volt, így a különböző multiplikatív struktúrák néhány nyelvhez tartozó számírásrendszerben nem jelennek meg.
Szavak és számértékek elkülönítése
[szerkesztés]Az adott szövegben a számszakaszokat a szavaktól rendszerenként és koronként is eltérő jellel különböztették meg, leggyakrabban a betűk fölé helyezett vonallal – görög számírás, héber számírás -, vagy pl. a numerikus szakasz két oldalán levő ponttal a gót számírás esetén. Idővel egy újabb diakritikus jelet, az aposztrófot, ’, használták fel, ezt helyezték a görögök az első számjel bal oldala mellé.
A gót alfabetikus számírással írva 285-öt, a két oldalt levő ponttal elkülönítve a szövegtől:
Az etióp számírásban a számjel alatt és felett levő vonal mutatja, hogy az numerikus értékkel bír, bár az etióp számírás az a kivétel, amelyiknél a számjelek nem a saját írásuk betűi. A szavak és számok elkülönítésének ez a gyakorlata náluk csak az i. sz. 15. századtól létezett.[4]
Az etióp számírás számjelei:
1 2 3 4 5 6 7 8 9 × 1 ፩ ፪ ፫ ፬ ፭ ፮ ፯ ፰ ፱ × 10 ፲ ፳ ፴ ፵ ፶ ፷ ፸ ፹ ፺ × 100 ፻ × 10.000 ፼
Számírás iránya
[szerkesztés]A számírások iránya követte az adott nyelv írásrendszerének irányát, így a görög, kopt, etióp, gót, grúz, örmény, cirill számírásokban balról jobbra vezet, azaz a 10 legmagasabb hatványa bal oldalt áll és jobbfelé csökkenő sorrendben írták a kisebb hatványok számjegyeit, míg a héber, arab abdzsad, szír írásokban jobbról balra.
Betűsorrend
[szerkesztés]A görög alfabetikus, a kopt, gót, héber, szír, örmény, grúz, glagolita és latin rendszerek mind felhasználják saját ábécéjük sorrendiségének az előnyét, a számok hozzárendelésénél követik írásuk betűsorrendjét. Viszont az arab abdzsad számírás esetén az arab, valamint a cirill számírásnál is a cirill betűkhöz rendelt számértékek nem felelnek meg a szokásos betűsorrendnek. A fez számok és a zimám számírás egybeolvadt alfabetikus rendszerek, melyek két vagy több létező alfabetikus számírásrendszert ötvöznek, hogy egy új számírásrendszert hozzanak létre, melyben a számok sora egyik írásrendszer jelsorrendjéhez sem illeszkedik. Végül az etióp rendszernél az etióp numerikus jelek nem az etióp írás – Ge’ez – betűi, hanem a görög, ill. a kopt betűkből eredeztethetők.[5]
Törtek
[szerkesztés]Egységtörtek
[szerkesztés]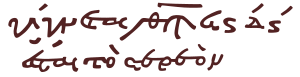
A törtek ábrázolására használták az egységtörteket. A görögök esetén a számjelet követő aposztróf (ʹ) jelölte, hogy az egységtörtként értelmezendő, azaz a számjel volt a tört nevezője a számláló pedig 1; így pl. a γʹ egyharmadot, a δʹ egynegyedet jelölt.
Az egységtörtek additívak voltak – mint az egyiptomi törtek –, így például az 5⁄12 -et a következőképp ábrázolták:
- δʹ ϛʹ = 1⁄4 + 1⁄6 = 5⁄12
További példa az egységtörtekkel való számábrázolásra:
- ͵θϡϟϛ δʹ ϛʹ = 9996 + 1⁄4 + 1⁄6
Csillagászati törtek
[szerkesztés]
A decimális rendszerek mellett az ókori és középkori csillagászok a csillagászati számításokban a törtekre külön szexagezimális rendszert használtak. Ebben kombinálva a hagyományos alfabetikus számírásokat a hatvanas alapú helyiértékes elvvel, melyet a görögök a babiloni csillagászoktól vettek át.
A babiloni csillagászok és matematikusok i. e. 2100-tól kezdődően egy kumulatív-helyiértékes, 60-as alapú és 10-es alrendszerű számírásrendszert használtak. A 60-nál kisebb számokat a 10 (![]() ) és az 1 (
) és az 1 (![]() ) ékírásjelének kumulatív kombinációjával ábrázolták, míg a 60 hatványait (60, 3600, 216 000, …) a helyiértékes elv bevonásával. I. e. 3. század körülre a görögök az addig babiloni befolyás alatt álló területeket kontrolljuk alá vonták a Nagy Sándor hódításai nyomán született Szeleukida Birodalomban. Ezt követően i. e. 3. és 1. század között a görögök a babiloni helyiértékes hatvanas alapú rendszert összeházasították a görög alfabetikus rendszerrel és ettől kezdődően a görög csillagászok a törtekre ezt használták.
) ékírásjelének kumulatív kombinációjával ábrázolták, míg a 60 hatványait (60, 3600, 216 000, …) a helyiértékes elv bevonásával. I. e. 3. század körülre a görögök az addig babiloni befolyás alatt álló területeket kontrolljuk alá vonták a Nagy Sándor hódításai nyomán született Szeleukida Birodalomban. Ezt követően i. e. 3. és 1. század között a görögök a babiloni helyiértékes hatvanas alapú rendszert összeházasították a görög alfabetikus rendszerrel és ettől kezdődően a görög csillagászok a törtekre ezt használták.
A csillagászati törtek (görög) számjelei minuszkula betűkkel:
1-esek α β γ δ ε ϛ ζ η θ 1 2 3 4 5 6 7 8 9 10-esek ι κ λ μ ν 10 20 30 40 50
͵αφιε κ ιε = 1515 + (20 x 1/60) + (15 x 1/3600) = 1515,3375
A rendszerben az egész számokat mindig a decimális alfabetikus rendszerrel írták, míg a törteket szexagezimális helyiértékes írással. A törtek különböző helyiértékeinek 1 és 59 közötti számaira a görög alfabetikus számok tizennégy számjelét használták (1-9-ig az egységjeleket és a tízesekből 10-től 50-ig). A babiloni rendszertől eltérően viszont a görög hatvanas számrendszerrel sosem éltek az egész számok ábrázolásánál. A törtek helyiértékes írásánál használták viszont a helypótlót, amit a görögök szintén a babiloniaktól vettek át – a babiloni helyiértékes számírás késői példáiban ezt már használták. A szexagezimális törteket bármilyen tört értékének jelölésére alkalmazhatták; az egymás utáni helyiértékek az 1/60, 1/602, 1/603 … etc. értékeit jelölték, amilyen kis értéket ki akartak fejezni. Nem használtak viszont radix pontot – tízes alapú helyiértékes rendszerben tizedesvessző lenne – az egész értékek és törtszámok elkülönítésére.
A szexagezimális számírás megfelelt a görög csillagászatnak, ahol ugyanúgy mint ma is, a kör 360 fokra volt osztható, mindegyik fok hatvan szögpercre, és mindegyik szögperc 60 szögmásodpercre, etc.
Egy példa a csillagászati törtekre: Alexandriai Theón (i. sz. 4. sz.) Ptolemaiosz Syntaxisáról írt munkájában a következő jelek:
- ͵αφιε κ ιε
- 1515 (͵αφιε) fokot, 20 (κ) percet és 15 (ιε) másodpercet jelentenek.[6] A fokokat a tízes alapú alfabetikus számírással, míg az utolsó két pozíción levő értékeket szexagezimálisan írta.
A szexagezimális törtek szabálya bármelyik alfabetikus rendszerrel kombinálható volt, az 1 – 59-ig terjedő görög jeleket az adott rendszer számjeleivel behelyettesítve. Az arabok a görögök után, az i. sz. 7. század közepén Mezopotámia felett megszerzett kontrolljuk következtében megörökölték a görög csillagászati ismeretek nagy részét is. Átvették a szexagezimális törtek használatát is, viszont az arab abdzsad jeleit használták és nem a görög alfabetikus számjeleket. Ehhez hasonlóan a középkori héber csillagászok is átvették a szexagezimális törteket, mint ez Lévi ben Gerson 14. századi munkáiban látható.[7]
A görög csillagászati szövegek arab fordításával jutottak el a szexagezimális – hatvanas alapú – helyiértékes számok i. sz. 1000 körülre Nyugat-Európába is.[8] Ettől kezdődően a középkori európai csillagászok a törtekre szexagezimális notációt használtak, sőt az Alfonz-táblázatoknak 1327-es párizsi szerkesztésű változatában még az egész számokat is szexagezimálisan jelölték. De még Afrikában is használták, a középkori etióp csillagászok szintén szexagezimális törtekkel írtak saját számításaikban és a görög és arab munkák fordításaiban is.[9]
Története
[szerkesztés]Kialakulása
[szerkesztés]Nincs egyetértés az alfabetikus számírás eredetét illetően:
- Korábbi elméletek szerint az első alfabetikus számírás a hébereknek köszönhető, a héber számírásnak egy i. e. 9. -7.- századi független eredetet valószínűsítenek,[10][11][12] melyek újabb kutatások szerint már nem hitelesek.[13]
- G. Ifrah vélekedése szerint kulturális kereszthatásoktól függetlenül alakult ki, posztulál egy i. e. 8. 9. századi eredetet, melyre viszont nem léteznek bizonyítékok.
- Az alfabetikus számírás S. Chrisomalis szerint az i. e. 6. századból a görögöktől eredeztethető, akik az egyiptomi demotikus számírásrendszert és saját fonetikus írásjeleik számjelekként való használatát ötvözték, szintén a demotikus számírásból vették át az egy adott szint feletti multiplikatív-additív struktúrát.[14]
Elterjedése
[szerkesztés]Alfabetikus számírásrendszereket használtak egészen északon, Angliában, Germániában, Oroszországban, és egészen délen is, pl. Etiópiában, Észak-Afrikában, Marokkótól keletre is, valamint a Közel-Keleten egészen Iránig.
A görög alfabetikus számírás legtöbb származéka saját írásuk betűivel helyettesítette a görög jeleket. Az i. e. 2. század vége felé a héberek a görög modell alapján fejlesztették ki a héber alfabetikus számírást. Az i. sz. 4. század közepén a gótok alakítottak ki egy saját alfabetikus számírást, míg a görög hatás alatt álló Észak-Afrikában, az egyiptomi kopt írás és az etiópiai Ge’ez írás mellett született a görög modell alapján alfabetikus számírás. Örményországban és Grúziában a Bizánci Birodalom határán írások és alfabetikus számírások fejlődtek ki az i. sz. 5. században, megközelítőleg a kereszténység felvételével egyidőben. Az i. sz. 6. században a szír írás megvált a korai kumulatív-additív számírásától egy, a görög rendszerre alapozott kedvéért. Megközelítőleg ugyanebben az időben jelent meg az arab abdzsad számírás, melyet az iszlám hódítást követően a Közel-Keleten használták. Az i. sz. 9. században a szláv területeken kialakult glagolita és a cirill számírás, mely a Cirill és Metód által kifejlesztett írás égisze alatt született. Végül a görög alfabetikus számírás megismerése vezetett egy latin alfabetikus számírás kifejlesztéséhez az. i. sz. 12. században.[15]
Hét alfabetikus számírásrendszert ezer évig, vagy még tovább is használtak – ez a görög, kopt, etióp, arab abdzsad, héber, szír, örmény és grúz számírás -. A görög rendszer esetében ez használóinak a politika jelentőségével is magyarázható, de másoknál, mint a héber és az örmény, a rendszerek használói nagymértékben politikailag és kulturálisan is marginalizálódtak. Hogy ezek a rendszerek mégis ilyen körülmények között is fennmaradtak, és olyan helyen is, ahová már a helyiértékes rendszer is eljutott, részben strukturális jegyeivel magyarázható:
- Az alfabetikus rendszerek „alfabetikussága” alapján az írásjelek mellé nem kellett még egy számírásjelkészletet is megtanulni.
- Az alfabetikus rendszerek tömörebbek még a helyiértékes rendszereknél is, ugyanis bármelyik helyiértékes numerikus szakasz tartalmazhat zérót is.
- Egy sokkal kielégítőbb magyarázat szerint az alfabetikus számírásrendszerek, ugyanúgy mint az írás is, a kulturális identitás jelentős markerei. Több esetben (pl. kopt, gót, örmény, grúz, glagolita és cirill számírás) egy szűk csoport fejlesztette ki saját írásukat és ezzel egyidőben az egyedi alfabetikus számírásukat is. Az alfabetikus számírások nem nyelvfelettiek, hanem az írásrendszerek szerves részévé váltak.[16]
Felváltása
[szerkesztés]A helyiértékes számírás megjelenésével az alfabetikus számírásrendszerek szerepe, használatának kontextusa beszűkült. Amikor alkalmazásuk rendszeres használata megszűnt, sokat közülük korlátozottabb funkciókra, de továbbra is használták, különösen egy adott vallás hazájában (pl. héber, szír, kopt, görög, cirill). Az elmúlt öt évszázad masszív globalizációja fényében a nyugati és az arab helyiértékes számírás vált a legkorábbi standard rendszerré, melyet majdnem mindenki megtanult. Az alfabetikus számírások jövője így egyre inkább kérdésesnek tűnik.
Gematria
[szerkesztés]A görögök, héberek és az arabok az alfabetikus számírásukat a gematriahoz, azaz a számmágia módszeréhez is felhasználták. Ennek alapja, hogy nemcsak az írás minden betűje bír számértékkel is, hanem így minden szónak is van numerikus értéke is, mely a betűk számértékének összegével egyenlő.
A héberek esetén a gematria az egyik fontos funkció volt, melyre a héber számokat a történelmükben használták.[17] A középkori és a modern kor eleji tudósok ezt a gyakorlatot általánosan alkalmazták a Talmud és Midrás egyes részeinek értelmezésére, azzal a céllal, hogy szimbolikus jelentést találjanak a szavak és az azoknak megfelelő számértékek között.
Ehhez kapcsolódó gyakorlat a kronogramma készítése is, amelyben az adott szavak számértékei egy esemény dátumával megegyezők. Ez a használat is, melyet az arab abdzsad is gyakorolt – arab megnevezése hisab al-adjummal-,[18] hozzájárulhatott jóval a helyiértékes rendszer átvétele után is az alfabetikus számírás fennmaradásához.[19]
Alfabetikus számírásrendszerek
[szerkesztés]- Görög alfabetikus számírás – gyakran „ion” vagy „milétoszi” rendszernek is nevezik Kis-Ázsia nyugati részéről való eredete miatt. Az első bizonyítékok az i. e. 6. századra tehetők, melyeket Kária ion városaiban – pl. Milétosz – használt archaikus görög írás betűivel írták, struktúráját közvetlenül az egyiptomi demotikus számírásból vették át.[20] Története során a számírást széles kontextusban – gazdasági dokumentumokon, emlékműveken, csillagászati, matematikai munkákban – használták. A legtöbb görög matematikai munkában alfabetikus számok állnak, melyeket az összes görög matematikus Arkhimédésztől kezdve Apollónioszig használt. A görög alfabetikus számírással egész története alatt elsősorban görög nyelvterületeken, vagy görög nyelvűek kontrollja alá eső régiókban írtak. Korai történetében a rendszert a kelet Mediterráneumban a Ptolemaioszi Egyiptomban és a Szeleukida Perzsiában is használták. A Római Birodalomban adminisztratív céllal nem alkalmazták, de a Bizánci Birodalomban már igen, viszont 1453-tól, Konstantinápoly eleste után, az adminisztratív funkció elhalt. Ugyanakkor ezután is alkalmazták korlátozott céllal, oldalszámozására, vagy listák sorszámozására, ugyanúgy, ahogy a római számokat a korabeli Nyugat-Európában. Az alfabetikus számokat számos görög bibliában fejezetek és versek számozására ma is használják, valamint bizonyos jogi környezetben és oldalszámozásra is.
- Kopt számírás – a kopt írás mellett Egyiptomban az i. sz. 4. században a görög alfabetikus számírás mintájára megszületett a kopt számírás,[21][22] melynek számjelei hasonlítanak az i. sz. 4. és 9. század közötti görög unciális jelekre. A kopt számok napjainkban is használatban vannak a kopt ortodox egyház liturgiai szövegeiben oldalszámozásra és sztichometriai célból.
- Zimám számírás – Egyiptomban az i. sz. 10. században kialakult számírás, a rendszer struktúrájában azonos a klasszikus kopt rendszerrel, de a numerikus jelek kurzív minuszkula betűk és nem unciálisak. Széleskörű kontextusban – elsődlegesen gazdasági dokumentumokban – hosszan megtartott használatuk okán lényegesen nagyobb jelentőségűnek számít, mint a beszűkült funkciójú unciális kopt számírás. A zimám számokat használók egyiptomi kopt keresztények voltak, de ez nem volt kőbevésett szabály, így egyiptomi héber és muszlim arab nyelvű írásokban is rendszeresen használták a zimám számokat az arab abdzsad, ill. a héber alfabetikus számírás helyett.[23] Használatuk túlélte Egyiptomnak az Oszmán Birodalom általi 1517-es meghódítását, csak a 17. században szűnt meg, amikor az arab helyiértékes számok átvették a szerepüket.[24]
- Etióp számírás – legkorábbi példája egy i. sz. 3. század végéről való sztélén áll. Az etióp numerikus jelek nem az etióp írás – Ge’ez – betűi, hanem a görög, ill. a kopt betűkből betűkből eredeztethetők, a számjeleknek így nincs az etióp írásban nemnumerikus jelentése is, mégis a számjel alatt és felett levő vonal mutatja, hogy az numerikus értékkel bír. A rendszer karakterkészlete csak tizennyolc jelből áll, efölött -100 fölött – már multiplikatívan ábrázolták a számokat. Az Akszúmi Királyság bukása után, az iszlám hódítás következtében az etióp írást csak ritkán használták, idővel ezoterikusnak számított, csak tudósok és az etióp ortodox egyház papjai ismerték. Matematikai, numerológiai és csillagászati szövegekben a középkori Etiópiában mind az egész számokat, mind a törtszámokat is az etióp számírással ábrázolták.[25] Az amhara nyelven írt szövegekben az etióp számokat széles kontextusban használták a 15. századtól napjainkig.[26] A modern etióp számírás struktúrája csak enyhén módosult, jelenleg még mindig használják alkalmanként dátumozásnál.[27][28]
- Gót számírás – a gótok az i. sz. 350 körül Wulfila püspök által kifejlesztett gót ábécé mellett kialakították a gót alfabetikus számírást is.[29] Az i. sz. 7., ill. a 8. században kezdett írásuk és számírásuk használata megszűnni, és felváltotta az ekkor egész Nyugat-Európában ismert római számírás.
- Héber alfabetikus számírás – az i. e. 2. századra a héber írás betűiből születtek meg az egyedi héber alfabetikus számok,[30] melyeknek az i. e. 125 és 100 közötti Hasmoneus érmék feliratai korai bizonyítékai.[31][32] Azok a korábbi elméletek, melyek egy sokkal korábbi, i. e. 9. -7.- századi független eredetet valószínűsítenek[10][11][12] S. Chrisomalis szerint már nem hitelesek. A héber számírás az íráshoz hasonlóan jobbról balra íródik. A modern Izraelben a legtöbb funkcióra a nyugati számírást használják, viszont a hagyományos héber kalendárium dátumaiban, különösen vallásos szövegekben és sírfeliratokon az alfabetikus számok is rendszeresen előfordulnak.[33]
- Szír alfabetikus számírás – valószínűleg az i. sz. 6. században alakulhatott ki, fokozatosan váltotta fel az ószír rendszert az elkövetkező két évszázad során.[34] Perzsia nesztoriánus keresztényei és Szíria jakobita keresztényei által használt kaldeus és certó írás mellett használták az alfabetikus számírásrendszert.[35] A rendszer jobbról balfelé íródik, a számokat a betűktől a numerikus szakaszok fölé írt vízszintes vonal különbözteti meg. A héber alfabetikus számíráshoz hasonlóan 22 jellel bír, az 500 és 900 közötti értékeket az alacsonyabb százas értékek és a 400-as jelének különböző additív kombinációjával képezték, ill. a nagyobb százas értékeket alkalmanként multiplikatívan jelölték, az 50 és 90 közötti értékek fölé pontot helyezve.[36][37] Szír számok csak nagyon gyéren találhatók monumentális kőfeliratokon vagy érméken. Viszont vallásos szövegekben használatuk nagymértékben elterjedt kifejlesztésétől egészen a mai napig is, a helyzet oka a jakobiták és a nesztoriánusok viszonylagos elhatárolódása a görög és a római kereszténységtől. A legtöbb szír vallásos szöveg oldalszámozásánál és a dátumozásánál a szír számokat használják.
- Arab abdzsad számírás – lehetséges, hogy iszlám előtti gyökerei vannak, de valószínűbb egy i. sz. 650 körüli eredet. A 8. század végére az arab abdzsad számok az egész Közel-Keleten elterjedtek, valamint a magrebi régióiban és az Ibériai-félsziget déli részén is. Adminisztratív dokumentumokban, irodalmi és tudományos szövegekben, érmék és feliratok dátumain használták. Röviddel az abdzsad számok kifejlesztése után, kiszorította azt a hinduktól átvett, jól ismert arab cifferes-helyiértékes számírás, melyet arab nyelven al-hisab al-hindi-ként ismertek. A helyiértékes számírás bevezetése ellenére is a csillagászok sokkal tovább használták az abdzsad számokat, mivel átültették azokat a kvázi-helyiértékes törtszámok használatára. A 13. század végéig az összes csillagászati és asztrológiai szövegben csak abdzsad számok álltak, és több évszázaddal ezt követően is még az abdzsad és a helyiértékes számok egymás mellett szerepeltek egy adott szövegben. Korlátozott céllal mind a mai napig fennmaradt, kriptografikus, irodalmi és mágikus funkciókra, mint pl. a kronogramma, valamint előszavak, táblázatok, könyvek tartalomjegyzékének oldalszámozására, ugyanúgy, mint ahogy a nyugati világban a római számokat használják.[38][39]
- Fez számírás – a fez számírás legkorábbi változatát a mozarabok használták Toledoban, Spanyolországban a 12. és 13. században[40] Később a modern Marokkó Fez városa körül is a 16. századtól kezdődően felbukkan, a számírás eltért mind az arabtól mind a görögtől is. A rendszert hisad al-qualam al-Fasi néven, ill. rumi (bizánci) jelekként ismerték. A rendszer 27 írásjellel bír, jobbról balra íródik. Marokkóban a gyarmatosítás utáni változások vetettek véget a rendszer használatának.
- Örmény számírás – az alfanumerikus számírás elvét ők is a görögöktől vették át. Nem tisztázott, hogy az örmény számírást is Meszrop Mastoc maga, vagy tanítványa, az i. sz. 5. század kezdetén fejlesztette-e ki, avagy még ugyanabban az évszázadban valamennyivel később hozták létre.[41] Az ősi, harminchat betűből álló örmény ábécé elegendő jellel szolgált 1-től 9000-ig a teljes számsorhoz, ugyanakkor a többi alfabetikus rendszertől eltérően az örmény rendszerben nem éltek a magasabb értékeknél multiplikatív elvvel, ezeket lexikális számokkal írták ki. A cifferes-helyiértékes számírással Örményországban először az i. sz. 12. sz-ban írtak,[42] viszont az örmény írástudók az alfabetikus számokat a legtöbb általános célra még jóval ezután is megtartották, néha még ma is használják az Újtestamentum fejezeteinek számozására.[43]
- Sirakaci számírása – az örmény ábécé tizenkét jelére Sirakaci örmény matematikus az i. sz. 7. században kifejlesztett egy számírásrendszert, ezt Aritmetika c. könyvében (T’aubant’iwn) írta le. Más vélekedés szerint a rendszert nem Shirakatsi alkotta, hanem létezett egy általánosan használt változata, melynek Shirakatsi munkája az egyedüli fennmaradt folyománya.[44] A rendszert matematikai és csillagászati számításokban használhatták, alapformája tizenkét jelet használ.[45] Az egyes jelek azonosak az örmény hagyományos rendszerben használtakkal, az egységjeleket viszont a tíz 3 hatványa követi (10, 100, 1000), a többi számot multiplikatív és additív módon ábrázolják.
- Grúz számírás – a kereszténység felvétele után az örményekhez hasonlóan a grúzok is a görög alfabetikus rendszert modellként tekintve kifejlesztettek egy írást és számírásrendszert. A grúz számokat irodalmi és vallásos szövegekben az egész középkorban használták, különösen oldalszámozásra, dátumok jelölésére, sztichometriai céllal és monumentális kőfeliratokon is. Rendszeres használata a 16. században lezárult, amikor a grúzok az Oszmán Birodalom ellenőrzése alá kerültek, ettől kezdve az arab helyiértékes számokat használták adminisztratív és kereskedelmi célokra is, bár az alfabetikus számírásuk fennmaradt vallási tárgyú írásokban.[46]
- Glagolita számírás – az i. sz. 860 és 870 között Cirill és Metód által, az ószláv keresztény írások számára kifejlesztett glagolita ábécéhez kapcsolt számírás.[47] A 15. század körüli időkre szinte az összes szláv nép vagy a római, vagy a cirill számírást adoptálta, csak a horvát katolikus liturgiát megőrző Horvátországban, különösen az Adriai partok mentén – Dalmáciában – használták továbbra is a glagolita írást és számírást.[48][49]
- Cirill számírás – az i. sz. 890-900-ban kifejlesztett cirill írást eredetileg az ószláv egyház írásaira használták, később a különböző szláv nyelvek írására is átvették, leginkább az oroszra. Ehhez egy alfabetikus számírásrendszert megközelítőleg ugyanebben az időben alakítottak ki. A cirill számírásrendszer az i. sz. 10. században jutott el a Kijevi Orosz Fejedelemséghez.[50] Oroszországban még a 18. század folyamán is az arisztokratáknak, hivatalnokoknak mind a római, a helyiértékes és a cirill számírásban is jártasnak kellett lenniük, hogy a különböző műfajok teljes skálájú szöveganyagát olvasni tudják. Egészen későn, 1918-ban Alexandra cárné utolsó naplójának oldalszámozását ezekkel írta, ez mutatja, a cirill számoknak még ekkor is volt jelentősége, még ha az utolsó cári korszakban egyre inkább csak formális.[50]
- Latin számírás – a 11. századtól kezdődően az arabok által lefordított görög csillagászati munkákat kezdték latinra is fordítani, így a nyugat-európai tudósok egyre nagyobb mértékben ismerték meg a görög számírást. Egy maroknyi szövegben kísérletet tettek a görög alfabetikus számírásnak, ill. arab abdzsad számoknak a latin ábécét felhasználó konvertálására, a latin ábécé akkor létező huszonkét betűjét használva az 1-től 9-ig, 10-től 90-ig, ill. 100-tól 400-ig terjedő számokhoz rendelve.[51] Nem ismert a 13. századból vagy későbbi dokumentumokból a rendszer használata.
Jegyzetek
[szerkesztés]- ↑ Stephen Chrisomalis. Numerical Notation: A Comparative History. Cambridge University Press, 184. o. (2010). ISBN 9780521878180. Hozzáférés ideje: 2019. április 5.
- ↑ S. Chrisomalis 133. old.
- ↑ Heath 1921: 39-41. old)
- ↑ Ifrah: 246-247. old.
- ↑ S. Chrisomalis 186. old.
- ↑ Thomas, Ivor. 1962. Selections Illustrating the History of Greek Mathematics, vol. 1. Cambridge, MA: Harvard University Press. 50-51. old.
- ↑ Georges Ifrah. The universal history of numbers: from prehistory to the invention of the computer; translated from the French by David Bellos. London: Harvill Press, 158. o. (1998). ISBN 9781860463242
- ↑ Neugebauer
- ↑ Neugebauer 1979
- ↑ a b Smith and Karpinski 1911: 33. old.
- ↑ a b Gandz 1933: 75-76. old.
- ↑ a b Schanzlin 1934
- ↑ S. Chrisomalis
- ↑ S. Chrisomalis 185. old.
- ↑ S. Chrisomalis 146. old.
- ↑ S. Chrisomalis 187. old.
- ↑ Ifrah 1998: 250-256.old.
- ↑ Colin 1971: 468. old.
- ↑ S. Chrisomalis 159. old.
- ↑ S. Chrisomalis 140. old.
- ↑ Megally 1991
- ↑ Messiha 1994
- ↑ S. Chrisomalis 150. old.
- ↑ Messiha 1994: 26. old.
- ↑ Neaugebauer
- ↑ Pankhurst
- ↑ Bender 1976: 124. old.
- ↑ S. Chrisomalis 154. old.
- ↑ Braune and Ebbinghaus 1966: 10. old.
- ↑ Stephen Chrisomalis 156. old.
- ↑ Gandz 1933: 76.old.
- ↑ Millard 1995: 192. old.
- ↑ S. Chrisomalis 159. old.
- ↑ Duval, Rubens. 1881. Traite de grammaire syriaque. Paris: Vieweg. 15. old.
- ↑ Daniels, Peter T. and William Bright, eds. 1996. The World's Writing Systems. New York: Oxford University Press.
- ↑ Duval, Rubens. 1881. Traite de grammaire syriaque. Paris: Vieweg. 15. old.
- ↑ Nöldeke, Theodor. 1904. Compendious Syriac Grammar. Translated by James A. Crichton. London: Williams and Norgate. 316-317. old.
- ↑ Colin 1960: 97. old.
- ↑ S. Chrisomalis 162. - 167. old.
- ↑ S. Chrisomalis 171. old.; Colin, Georges S. 1933. De l'origine grecque des "chiffres de Fes" et de nos "chiffres arabes". Journal Asiatique 222: 193-215. 204. old.
- ↑ S. Chrisomalis 174. old.
- ↑ Shaw 1938-39: 368. old.
- ↑ S. Chrisomalis 175. old.
- ↑ Shaw 1938-39: 369. old.
- ↑ Shaw 1938-39: 270. old.
- ↑ S. Chrisomalis 177. old.
- ↑ S. Chrisomalis 178. old.
- ↑ S. Chrisomalis 180. old.
- ↑ Cubberley 1996: 350. old.
- ↑ a b S. Chrisomalis 182. old.
- ↑ S. Chrisomalis 183. old.
Források
[szerkesztés]- Stephen Chrisomalis. Numerical Notation: A Comparative History. Cambridge University Press, 133-187. o. (2010). ISBN 9780521878180
- Georges Ifrah. The universal history of numbers: from prehistory to the invention of the computer; translated from the French by David Bellos. London: Harvill Press (1998). ISBN 9781860463242
- Heath, Thomas L.. A History of Greek Mathematics. 2 vols.. Cambridge: Cambridge University Press. (1921)
- Otto Neugebauer. Ethiopic Astronomy and Computus. Wien: Verlag der Österreichischen Akademie der Wissenschaften (1979)
- Megally, Fuad. Numerical system, Coptic, 1820-1822. o. (1991).
- Messiha, Heshmat. 1994. Les chiffres coptes. Le Monde Copte 24: 25-28.
- Braune, Wilhelm and Ernst Ebbinghaus. 1966. Gotische Grammatik. Tubingen: Max Niemeyer Verlag.
- Gandz, Solomon. 1933. Hebrew numerals. Proceedings of the American Academy of Jewish Research 4: 53-112.
- Millard, A. 1995. Strangers from Egypt and Greece – the signs for numbers in early Hebrew. In Immigration and Emigration within the Ancient Near East, K. van Lerberghe and A. Schoors, eds., pp. 189–194. Leuven: Peeters.
- Colin, G.S. 1960. Abdjad. In Encyclopedia of Islam, vol. 1, pp. 97–98. Leiden: Brill.
- Colin, G.S. 1971. Hisab al-djummal. In Encyclopedia of Islam, vol. 3, p. 468. Leiden: Brill.
- Bender, Marvin L., Sydney W. Head, and Roger Cowley. 1976. The Ethiopian writing system. In Language in Ethiopia, M.L. Bender, J.D. Bowen, R.L. Cooper, and CA. Ferguson, eds., pp. 120–129. London: Oxford University Press.
- Shaw, Allen A. 1938-9. An overlooked numeral system of antiquity. National Mathematics Magazine 13: 368-372.
- Cubberley, Paul. 1996. Tlie Slavic alphabets. In The World's Writing Systems, Peter T. Daniels and William Bright, eds., pp. 346–355. New York: Oxford University Press.
- Pankhurst, Richard K.P., ed. 1985. Letters from Ethiopian Rulers (Early and Mid-Nineteenth Century), translated by David L. Appleyard and A.K. Irvine. Oxford: Oxford University Press.
- Smith, David E. and L. C Karpinski. 1911. The Hindu-Arabic Numerals. Boston: Ginn
- Gandz, Solomon. 1933. Hebrew numerals. Proceedings of the American Academy of Jewish Research 4: 53-112. old.
- Schanzlin, G.L. 1934. The abjad notation. The Moslem World 24: 257-261.



