Általános relativitáselmélet

A GW150914 kettős fekete lyuk rendszer lassú mozgású számítógépes szimulációja, ahogy egy közeli megfigyelő látja, végső becsavarodásának, egyesülésének és leeresztésének 0,33 másodperce alatt. A fekete lyukak mögötti csillagmező erősen torzult, ill. forgásban és mozgásban levőnek tűnik az extrém gravitációs lencsehatás miatt, amikor is maga a téridő torzult és felcsavarodott a forgó fekete lyukak körül.

Az általános relativitáselmélet Albert Einstein 1915-ben közzétett geometriai elmélete a gravitációról és egyben a gravitáció jelenleg elfogadott legpontosabb, kísérletekkel is ellenőrzött leírása a modern fizikában. Az általános relativitáselmélet tekinthető az összes létező fizikai elmélet közül a legszebbnek. Az általános relativitáselmélet általánosítja a speciális relativitáselméletet és a Newton-féle univerzális gravitációs törvényt, a gravitációt az egyesített tér és idő, azaz téridő, geometriai tulajdonságaként írja le. Pontosabban, a téridő görbülete közvetlenül kapcsolódik a bármely jelenlevő anyag és sugárzás energiájához és impulzusához. A pontos kapcsolatot az Einstein-féle mezőegyenletek határozzák meg, amely nemlineáris parciális differenciálegyenletek rendszere.

Az általános relativitáselmélet egyes előrejelzései jelentősen különböznek a klasszikus fizikától, különösen az idő múlása, a tér geometriája, a testek mozgása szabadesésben és a fény terjedése tekintetében. Ezekre a különbségekre példák a gravitációs idődilatáció, a gravitációs lencsehatás, a fény gravitációs vöröseltolódása és a gravitációs késleltetés. Az általános relativitáselmélet előrejelzései napjainkig minden eddigi megfigyelés és kísérlet során beigazolódtak. Habár az általános relativitáselmélet a gravitációnak nem az egyetlen relativisztikus elmélete, de ez a legegyszerűbb elmélet, amely konzisztens a kísérleti adatokkal. Megválaszolatlan azonban, hogy az általános relativitáselmélet hogyan egyeztethető össze a kvantumfizika törvényeivel, hogy a kvantumgravitáció teljes és önkonzisztens elméletét adja.

Einstein elméletének fontos asztrofizikai következményei vannak. Például megjósolja a fekete lyukak – olyan területek a térben, ahol a tér és az idő annyira eltorzultak, hogy semmi, még a fény sem szökhet ki –, mint a masszív csillagok végső állapotának létezését. Egyértelmű bizonyíték található arra, hogy bizonyos fajtájú csillagászati objektumok által kibocsátott intenzív sugárzást a fekete lyukak okozzák, például a mikrokvazárokat és az aktív galaxismagokat, melyeket a stelláris fekete lyukak, ill. nagyon nagy tömegű fekete lyukak létezése okoz. A fény gravitáció általi elhajlítása a gravitációs lencsehatás jelenségéhez vezet, amikor ugyanazon távoli csillagászati objektum többszöri képe látható az égbolton. Az általános relativitáselmélet előrejelzi a gravitációs hullámok létezését is, ezeket azóta a LIGO-Virgo együttműködés közvetlenül meg is figyelte. Ezen kívül az általános relativitáselmélet az alapja a táguló világegyetem jelenlegi kozmológiai modelljeinek.

Története

Nem sokkal a speciális relativitáselmélet 1905-ös publikálása után Einstein azon kezdett el gondolkodni, hogyan helyezhetné be a gravitációt az általa felvázolt relativisztikus keretbe. 1907-ben egy szabadon eső megfigyelőt magában foglaló egyszerű gondolatkísérlettel elkezdte a gravitáció relativisztikus elmélete utáni nyolcéves kutatást. Számos zsákutca és hibás kiindulópont után munkája, amit ma Einstein-féle mezőegyenletek néven ismerünk, 1915 novemberében a Porosz Tudományos Akadémia előtti előadásában csúcsosodott ki. Ezek az egyenletek meghatározzák, hogyan befolyásolja a benne jelenlévő anyag és sugárzás a tér és az idő geometriáját, ezek alkotják Einstein általános relativitáselméletének magját.

Einstein mezőegyenletei nemlineárisak és megoldásuk nagyon bonyolult. Elmélete kezdeti előrejelzéseinek kidolgozásánál Einstein közelítő módszereket használt, de már 1916-ban Karl Schwarzschild asztrofizikus megtalálta az Einstein-féle mezőegyenletekre az első nem triviális egzakt megoldást, a Schwarzschild-metrikát. Ez a megoldás alapozta meg a gravitációs összeomlás végső fázisainak, és a ma fekete lyukakként ismert objektumok leírását. Ugyanezen évben megtörténtek az első lépések Schwarzschild megoldásának általánosítására elektromosan töltött objektumok esetén, mely végül napjainkban az elektromosan töltött fekete lyukakkal összefüggő Reissner-Nordström-metrikát eredményezte. 1917-ben Einstein elméletét alkalmazta az univerzumra mint egészre, megnyitva a relativisztikus kozmológia területét. A kortárs gondolkodással összhangban egy statikus univerzumot feltételezett, és az eredeti mezőegyenleteihez egy új paramétert – a kozmológiai állandót – adott, hogy egyezzen ezzel a megfigyelési előfeltételezéssel. 1929-re azonban Hubble és mások megfigyelései megmutatták, hogy világegyetemünk tágul. Ezt pontosan leírták Alexander Friedmann 1922-ben felfedezett, kibővített kozmológiai megoldásai, amelyek nem igényelték a kozmológiai állandót. Georges Lemaître ezeket a megoldásokat használta az ősrobbanás-modellek korai változatainak kialakításához, amelyekben univerzumunk egy extrém forró és sűrű korábbi állapotból fejlődött ki. Einstein később a kozmológiai állandót élete legnagyobb baklövésének nevezte.

Ezen időszak alatt az általános relativitáselmélet csak egy érdekesség maradt a fizikai elméletek között. Egyértelműen felette állt a newtoni gravitációnak, konzisztens volt a speciális relativitáselmélettel, és számolt jó néhány, a newtoni elmélet által megmagyarázhatatlan hatással. Maga Einstein 1915-ben megmutatta, hogyan magyarázza meg elmélete a Merkúr bolygó perihéliumának anomáliás mozgását önkényes paraméter nélkül. Hasonlóképp egy 1919-es, Arthur Stanley Eddington által vezetett expedíció a Nap 1919. május 29-i teljes napfogyatkozása során megerősítette az általános relativitáselmélet előrejelzését a csillagok fényének elhajlásával kapcsolatban, ezzel Einstein egy csapásra híres lett. Mégis, az elmélet az elméleti fizika és asztrofizika fősodrába az 1960 és 1975 közötti időszak fejleményeivel került csak be, amit ma az általános relativitáselmélet aranykoraként ismerünk. A fizikusok kezdték megérteni a fekete lyuk elméleti modelljét, és a kvazárokat ezen objektumok asztrofizikai megjelenéseként azonosították. Egyre pontosabb naprendszeri kísérletek erősítették meg az elmélet előrejelzési erejét, és a relativisztikus kozmológia szintén alkalmassá vált közvetlen megfigyelési kísérletekre.

A klasszikus mechanikától az általános relativitáselméletig

Az általános relativitáselméletet a klasszikus fizikával való hasonlóságainak és különbözőségeinek a vizsgálatával lehet megérteni. Az első lépés annak a felismerése, hogy a klasszikus mechanika és Newton gravitációs törvénye megengednek egy mértani leírást. Ennek a leírásnak a kombinációja a speciális relativitáselmélettel az általános relativitáselmélet egy heurisztikus derivációját eredményezik.

A newtoni gravitáció geometriája

Az általános relativitáselmélet szerint a gravitációs mezőben található objektumok egy gyorsuló dobozban levő objektumokhoz hasonlóan viselkednek. Például egy megfigyelő a golyót ugyanúgy látja esni egy rakétában (balra), mint a Földön (jobbra), feltéve, hogy a rakéta gyorsulása egyenlő 9,8 m/s²-tel (ennyi a gravitáció okozta gyorsulás a Föld felszínén)

A klasszikus mechanika alapvetéseiben az a tétel jelenik meg, hogy egy test mozgása leírható a szabad (tehetetlenségi) mozgás és ezen szabad mozgástól való eltérés kombinációjával. Ezeket az eltéréseket Newton második mozgástörvényével összhangban a külső erő testre gyakorolt hatása okozza, amely kimondja, hogy a testre ható eredő erő egyenlő a test (tehetetlenségi) tömegével, szorozva a gyorsulásával. A kialakuló tehetetlenségi mozgások a tér és az idő geometriájához kapcsolódnak: a klasszikus mechanika hagyományos vonatkoztatási rendszerében az objektumok egy egyenes vonal mentén állandó sebességgel szabadon mozognak. Modernebbül megfogalmazva útjaik geodetikus vonalak, egyenes világvonalak a görbült téridőben.

Ennek megfelelően elvárható lenne, hogy az egykoron a testek aktuális mozgásának megfigyelésével és a külső erők (mint az elektromágnesesség vagy a súrlódás) figyelembe vételével meghatározott tehetetlenségi mozgások segítségével meghatározható mind a tér geometriája, mind egy idő koordináta. Azonban van itt egy kettősség, amint a gravitáció bekerül a képbe. Newton gravitációs törvénye alapján, és független kísérletekkel ellenőrizve, mint Eötvös Lorándé és követőié (ld. Eötvös kísérlet), a szabadesésnek van egy egyetemlegessége (ez gyenge ekvivalenciaelvként, vagy a tehetetlenségi és passzív-gravitációs tömeg univerzális egyenlőségeként is ismert): a próbatest pályája szabadesésben csak a helyzetétől és a kezdeti sebességtől függ, és nem anyagának bármely tulajdonságától. Ennek egyszerűsített változata testesül meg Einstein felvonókísérletében, a jobb oldali ábrán ábrázolva: egy kicsi, zárt szobában levő megfigyelő a testek, mint pl. egy leejtett golyó pályájának követésével nem képes eldönteni, hogy a szoba nyugalomban van-e egy gravitációs mezőben, vagy a szabad űrben található egy, a gravitációs mezőnek megfelelő gyorsulással gyorsuló rakéta fedélzetén.

Ha adott a szabadesés egyetemlegessége, akkor nem létezik megfigyelhető különbség a tehetetlenségi mozgás és a gravitációs erő hatására történő mozgás között. Ez sugallja a tehetetlenségi mozgás egy új fajtájának a meghatározását, mégpedig a gravitáció hatása alatt álló szabadon eső objektumokét. A kialakuló mozgások ezen új fajtája szintén meghatároz egy tér- és időgeometriát – matematikai kifejezéssel, ez olyan megadott konnekcióval kapcsolatos geodetikus mozgás, amely a gravitációs potenciál gradiensétől függ. A térnek ebben a szerkezetben még megvan a rendes Euklideszi geometriája. Azonban, maga a téridő sokkal bonyolultabb. Amint az bemutatható a különböző kísérleti részecskék szabadesési pályájának követéséből álló egyszerű gondolatkísérlettel, egy részecske sebességét jelölő téridő vektorok (idő-szerű vektorok) transzportálásának eredménye a részecske pályájával fog változni; matematikai kifejezéssel élve, a newtoni konnekció nem integrálható. Ebből vezethető le, hogy a téridő görbült. Az ebből eredő Newton-Cartan elmélet a newtoni gravitáció egy mértani megfogalmazása csak kovariáns fogalmakkal, azaz egy olyan leírás, amely bármely kívánt koordináta-rendszerben érvényes. Ebben a mértani leírásban, az árapályhatások – a szabadon eső testek viszonylagos gyorsulása – a konnekció deriváltjával kapcsolatosak, mutatva, hogy a módosított geometriát a tömeg jelenléte okozza.

Relativisztikus általánosítás

Fénykúp

Bármennyire is érdekes a mértani newtoni gravitáció, alapja, a klasszikus mechanika csak egy határesete a (speciális) relativisztikus mechanikának. A szimmetria nyelvén: ahol a gravitáció elhanyagolható, a fizika inkább a speciális relativitáselmélet Lorentz-invarianciájához áll közelebb, mint a klasszikus mechanika Galilei-invarianciájához. (A speciális relativitáselmélet meghatározó szimmetriája a Poincaré-féle csoport, amely transzlációkat, forgatásokat és boost-okat tartalmaz.) A kettő közti különbség jelentős lesz, amikor a fénysebességhez közelítő sebességekről és nagy energiájú jelenségekről van szó.

A Lorentz-szimmetriával további struktúrák jelennek meg. Ezeket fénykúpok sorozata határozza meg (lásd az ábrán). A fénykúpok kauzális struktúrákat definiálnak: minden egyes A eseményhez létezik egy olyan eseménykészlet, amelyek elvben vagy befolyásolhatják A-t, vagy befolyásolva lehetnek általa olyan jelek vagy kölcsönhatások útján, amelyeknek nem szükséges a fénynél gyorsabban haladni (mint pl. a B esemény a az ábrán), és egy olyan eseménykészlet, mely esetén az ilyen befolyásolás nem lehetséges (mint pl. a C esemény az ábrán). Ezek a készletek megfigyelő-függetlenek. A szabadon eső részecskék világvonalaival kapcsolatban a fénykúpok felhasználhatók a tér-idő fél-Riemann-metrikumának rekonstrukciójára, legalábbis egy pozitív skaláris tényezőig. Matematikai kifejezéssel, ez egy konformális struktúrát vagy konformális geometriát határoz meg.

A speciális relativitáselmélet a gravitáció mellőzésével van definiálva, így gyakorlati alkalmazása egy alkalmas modell, ha a gravitációt el lehet hanyagolni. A gravitációt behozva és a szabadesés egyetemlegességét feltételezve azonban egy, az előző szakaszhoz hasonló okfejtés érvényes: nincsenek globális inerciarendszerek. Helyette közelítő inerciarendszerek mozognak a szabadon eső részecskékkel együtt. A téridő nyelvébe lefordítva: az egyenes időszerű vonalak, amelyek a gravitációmentes inerciarendszert határozzák meg, egymáshoz képest görbült vonalakká deformálódnak, ami azt sejteti, hogy a gravitáció belefoglalása szükségessé teszi a változást a téridő geometriájában.

A priori, nem tiszta, hogy a szabadesés új lokális rendszerei egybe esnek-e a referenciarendszerekkel, amelyekben a speciális relativitáselmélet törvényei fennállnak – az elmélet a fény terjedésén alapul, és így az elektromágnesességen, aminek különböző lehet a kialakuló rendszerkészlete. De különböző feltételezéseket használva a speciális-relativitáselméleti rendszerekről (mint a földi-rögzített vagy szabadesésben levő) eltérő előrejelzések vezethetők le a gravitációs vöröseltolódásról, ami az a jelenség, ahogy a fény frekvenciája változik, amikor a fény egy gravitációs mezőn halad át (ld. lentebb). A jelenlegi mérések azt mutatják, hogy a szabadon eső rendszerek azok, amelyekben a fény úgy terjed, mint a speciális relativitáselméletben. Ezen állítás általánosítása, miszerint a speciális relativitáselmélet törvényei jó közelítéssel a szabadon eső (és nem forgó) vonatkoztatási rendszerekben is ugyanazok, Einstein ekvivalenciaelveként ismert, egy lényegi vezérelve a speciális relativitáselméleti fizikának a gravitáció befogadásánál.

Ugyanez a kísérleti adat mutatja azt is, hogy a gravitációs mezőben található órák által mért idő, a sajátidő nem követi a speciális relativitáselmélet szabályait. A téridő mértan nyelvén, nincs a Minowski-metrika által mérve. Mint a newtoni esetben, ez is egy sokkal általánosabb geometriát sejtet. Kis léptékben az összes szabadon eső vonatkoztatási rendszer egyenlő és közelítőleg Minkowski-féle. Tehát a Minkowski-tér görbült általánosításával van dolgunk. A metrikus tenzor, ami a geometriát meghatározza – pontosabban a hosszúságokat és szögeket hogyan mérjük – nem a speciális relativitáselmélet Minkowski-metrikája, hanem egy, fél- vagy ál-riemanni metrikaként ismert általánosítás. Továbbá minden riemanni metrika természeténél fogva társul egy bizonyos fajta konnekcióval, a Levi–Civita-konnekcióval, és ez tulajdonképpen az a konnekció, ami kielégíti az ekvivalenciaelvet és a teret lokálisan Minkowski-félévé teszi (azaz megfelelő lokális vonatkoztatási rendszerben a metrika Minkowski-féle, és első parciális deriváltjai és konnekciós együtthatói eltűnnek).

Einstein egyenletei

Miután a gravitáció hatásainak relativisztikus, geometriai változata meghatározásra került, a gravitáció forrásának a kérdése van hátra. A newtoni gravitációban a forrás a tömeg. A speciális relativitáselméletben a tömeg egy sokkal általánosabb mennyiség, az energia-lendület tenzor részévé válik, amely magába foglalja mind az energia, mind a lendület sűrűségeit, valamint a feszültséget (azaz a nyomást és a nyírást) is. Az ekvivalenciaelv alkalmazásával ez a tenzor már általánosítva van a görbült téridőre. Tovább építve a geometrikus newtoni gravitáció analógiájára, jogos az a feltételezés, hogy a gravitáció mezőegyenlete ehhez a tenzorhoz és a Ricci-tenzorhoz kapcsolódik, amely leírja az árapály hatások egy bizonyos fajtáját: egy kísérleti részecskékből álló kis felhő térfogatváltozását, melyek kezdetben nyugalomban vannak, majd szabadon esnek. A speciális relativitáselméletben az energia-lendület megmaradása megfelel annak az állításnak, hogy az energia-lendület tenzor divergenciamentes. Ez a képlet a parciális deriváltak görbült sokaságaikkal, a differenciálgeometria által tanulmányozott kovariáns deriváltakkal való helyettesítéssel már szintén létezik általánosítva a görbült téridőre. Ezzel a további feltétellel – miszerint az energia-lendület tenzor kovariáns divergenciája, és így bármi is legyen az egyenlet másik oldalán, nulla –, amit Einstein-féle (mező)egyenleteknek hívunk, a legegyszerűbb összessége az egyenleteknek:

$G_{\mu \nu }\equiv R_{\mu \nu }-{\textstyle 1 \over 2}R\,g_{\mu \nu }={8\pi G \over c^{4}}T_{\mu \nu }\,$

A bal oldal az Einstein-tenzor, a Ricci-tenzor $R_{\mu \nu }$ és a metrika specifikus divergenciamentes kombinációja, ahol $G_{\mu \nu }$ szimmetrikus. Pontosabban,

$R=g^{\mu \nu }R_{\mu \nu }\,$

a görbület skaláris. Maga a Ricci-tenzor az általánosabb Riemann-féle görbületi tenzorhoz így viszonyul

$R_{\mu \nu }={R^{\alpha }}_{\mu \alpha \nu }.\,$

Jobb oldalon a $T_{\mu \nu }$ az energia-lendület tenzor. Minden tenzor absztrakt index jelölésben van leírva. Az elmélet előrejelzéseinek összeegyeztetése alapján a bolygópályák megfigyelési eredményeivel (vagy, azonos módon az arról való meggyőződés, hogy a gyenge gravitációjú, alacsony sebességű határérték a newtoni mechanika), az arányossági állandó κ = 8πG/c⁴-ként rögzíthető, ahol G a gravitációs állandó és c a fénysebesség. Ha nincs jelen anyag, azaz az energia-lendület tenzor eltűnik, az eredmény a vákuumbeli Einstein-egyenletek,

$R_{\mu \nu }=0.\,$

Az általános relativitáselmélet alternatívái

Vannak az általános relativitáselméletnek olyan azonos előfeltételezésekre épülő alternatívái, amelyek további szabályokat és/vagy megkötéseket tartalmaznak, és eltérő mezőegyenletekhez vezetnek. Erre példák a Brans-Dicke elmélet, a távoli párhuzamosság, az f(R) gravitáció és az Einstein-Cartan elmélet.

Definíció és alapszintű alkalmazása

Az előző részben felvázolt levezetés tartalmaz minden információt az általános relativitáselmélet meghatározásához, tulajdonságainak leírásához, és a fizika alapvető fontosságú kérdéseinek megválaszolásához, miszerint hogyan használható az elmélet modellalkotásra.

Definíció és alapvető tulajdonságok

Az általános relativitáselmélet a gravitáció metrikaelmélete. Középpontjában az Einstein-egyenletek állnak, amelyek leírják a téridőt képviselő négy dimenziós, ál-Riemann-sokaság geometriája és az ebben a téridőben található energia-lendület közti összefüggést. Azok a jelenségek, amit a klasszikus mechanikában a gravitáció erejének tulajdonítunk (mint a szabadesés, a pályamozgás és az űreszközök pályái), az általános relativitáselméletben megfelelnek a téridő egy görbült geometriájában történő tehetetlenségi mozgásnak; nem létezik az a gravitációs erő, ami eltérítené az objektumokat saját természetes, egyenes útjukról. Ehelyett a gravitáció megfelel a tér és idő tulajdonságaiban bekövetkező változásnak, ami így megváltoztatja a lehetséges legegyenesebb utat, amit az objektumok természetszerűleg követnének. A görbületet ezáltal az anyag energia-lendülete okozza. John Archibald Wheeler által másképp megfogalmazva, a téridő megmondja az anyagnak, hogyan mozogjon, az anyag megmondja a téridőnek, hogyan görbüljön.

Míg az általános relativitáselmélet a klasszikus fizika skaláris gravitációs potenciálját egy szimmetrikus másodrendű tenzorral helyettesíti, ez utóbbi az elsővé egyszerűsödik bizonyos határértékeknél. Gyenge gravitációs mezők és a fénysebességhez képest alacsony sebességek esetén az elmélet előrejelzései közelítenek a Newton-féle gravitációs törvényéihez.

Mivel tenzorokból épül fel, az általános relativitáselmélet általános kovarianciát mutat: törvényei – és az általános relativitáselmélet keretein belül megfogalmazott további törvények – ugyanazt az alakot öltik fel minden koordináta-rendszerben. Ezen felül az elmélet nem tartalmaz semmilyen invariáns geometriai háttérstruktúrát, azaz háttérfüggetlen. Ezáltal eleget tesz a relativitás sokkal szigorúbb általános elvének, miszerint a fizika törvényei minden megfigyelő számára ugyanazok. Lokálisan, ahogy az ekvivalenciaelvben kifejezésre kerül, a téridő Minkowski-féle és a fizikai törvényei helyi Lorentz-invarianciát mutatnak.

Modellalkotás

Az általános relativisztikus modellalkotás lényegi alapja az Einstein-féle mezőegyenletek egy megoldása. Figyelembe véve az Einstein-féle mezőegyenleteket és az anyag tulajdonságaira alkalmazható egyenleteket, az ilyen megoldás egy bizonyos (általában bizonyos koordinátákkal megadott metrika által meghatározott) fél-Riemann-féle sokaságból, és az ezen sokaságon meghatározott bizonyos anyagi terekből áll. Az anyagnak és a geometriának ki kell elégítenie az Einstein-féle egyenleteket, pontosabban az anyag energia-lendület tenzorának divergencia-mentesnek kell lennie. Az anyagnak természetesen ki kell elégítenie bármely más egyenletet is, amely tulajdonságaira alkalmazandó. Összefoglalva, az ilyen megoldás egy modell-univerzum, ami kielégíti az általános relativitáselmélet törvényeit, és a bármely jelenlevő anyagra vonatkozó további törvényeket.

Az Einstein-féle egyenletek nemlineáris parciális differenciálegyenletek, és mint olyanoknak, nehéz egzakt megoldásukat megadni. Mindazonáltal számos egzakt megoldás ismert, bár csak néhányuknak van fizikai alkalmazásuk. A legismertebb egzakt megoldások, és egyben fizikai szempontból a legérdekesebbek is, a Schwarzschild-megoldás, a Reissner-Nordström megoldás és a Kerr metrika, ezek mindegyike megfelel egy bizonyos fajta fekete lyuknak az egyébként üres világegyetemben, és a Friedmann–Lemaître–Robertson–Walker, ill. de Sitter-világegyetem, ezek egy táguló világegyetemet írnak le. A nagy elméleti érdeklődésre számot tartó egzakt megoldások a Gödel világegyetem (amely a görbült térben megnyitja az időutazás érdekes lehetőségét), a Taub-NUT megoldás (egy homogén, de anizotróp modell-világegyetem), és az anti-de Sitter-tér (amely legújabban az ún. Maldacena-sejtés kapcsán került előtérbe).

Az egzakt megoldások megtalálásának nehézsége miatt az Einstein-féle mezőegyenleteket gyakran számítógépen numerikus integrálással oldják meg, vagy feltételezve az egzakt megoldások enyhe zavarát. A numerikus relativitáselmélet területén nagy kapacitású számítógépek vannak alkalmazva a téridő geometriájának a szimulációjára, és érdekes helyzetek, mint két összeütköző fekete lyuk Einstein-féle egyenleteinek megoldására. Alapvetően ezek a módszerek bármely rendszerre alkalmazhatók, ha adott az elegendő számítógépes erőforrás, és olyan alapvető kérdésekkel foglalkozhatnak, mint a meztelen szingularitások. Közelítő megoldások találhatók perturbációszámításokkal is, mint a linearizált gravitáció és általánosításai, a post-Newton-i tágulás, mely mindkettőt Einstein fejlesztette ki. Ez utóbbi egy olyan téridő geometriához kapcsolódó megoldás szisztematikus megoldását nyújtja, amelyben a fénysebességhez mérten lassú mozgású anyageloszlás található. A tágulás egy sor fogalmat érint; az első fogalom a newtoni gravitációt képviseli, miközben a későbbi fogalmak a newtoni elmélet általános relativitáselmélet okozta egyre kisebb korrekcióját képviselik. Ezen tágulás kibővítése a paraméteres post-Newton-i (PPN) formalizmus, amely lehetővé teszi az általános relativitáselmélet és az alternatív elméletek előrejelzései közti mennyiségi összehasonlítást.

Einstein elméletének következményei

Az általános relativitáselméletnek számos fizikai következménye van. Egyesek közvetlenül az elmélet axiómáiból erednek, míg mások csak az Einstein eredeti közzétételét követő sok év kutatómunkája által váltak világossá.

Gravitációs idődilatáció és frekvenciaeltolódás

Egy masszív test felszínéről elszökő fénysugár gravitációs vöröseltolódásának vázlatos bemutatása

Feltételezve, hogy az ekvivalenciaelv érvényes, a gravitáció befolyásolja az idő múlását. Az egy gravitációs kútba leküldött fény kékeltolódást szenved el, míg az ellenkező irányba küldött fény (pl. a gravitációs kútból feltörő) vöröseltolódást; gyűjtőnevükön ezt a két jelenséget gravitációs frekvenciaeltolódásnak nevezzük. Általánosabban, a masszív testhez közelebbi folyamatok sokkal lassabban mennek végbe a távolabb végbemenő folyamatokkal összehasonlításban; ez a hatás a gravitációs idődilatáció.

A gravitációs vöröseltolódást megmérték laboratóriumban és csillagászati megfigyelésekkel. Atomórák használatával a Föld gravitációs terében a gravitációs idődilatációt már számtalanszor megmérték, míg az állandó bizonyíték erre a Global Positioning System (GPS) egyik mellékhatása. Erősebb gravitációs terekbeli vizsgálatok kettőspulzárok megfigyelésével végezhetők. Minden eredmény összhangban áll az általános relativitáselmélettel. Azonban a jelen pontossági szint mellett ezek a megfigyelések nem tudnak különbséget tenni az általános relativitáselmélet és más olyan elméletek között, amelyekben az ekvivalenciaelv érvényes.

Fényelhajlás és gravitációs időkésleltetés

A (kékkel jelölt helyről kibocsátott) fény elhajlása egy (szürkével jelzett) kompakt test közelében

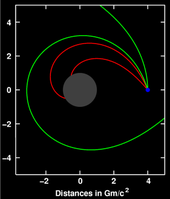
Az általános relativitáselmélet előrejelzi hogy a fény útja gravitációs mezőben meghajlik; egy masszív test mellett elhaladó fény a test felé hajlik. Ezt a hatást megerősítették a csillagok vagy távoli kvazárok fényelhajlásának megfigyelésével, miközben a Nap mellett elhaladnak.

Ez és a kapcsolódó előrejelzések abból a tényből következnek, hogy a fény az ún. fény-szerű vagy nullás geodetikát követik – a klasszikus fizikában jelenlevő, a fény által befutott egyenes vonalak egy általánosítása. Ilyen geodetikus vonalak a speciális relativitáselméletben a fénysebesség invarianciájának általánosítása. Ha megfelelő téridő-modelleket vizsgálunk (vagy a külső Schwarzschild-megoldást, vagy több mint egyetlen tömeg esetén a post-Newton-i tágulást), felmerül a gravitáció számos hatása a fény terjedésére. Bár a fény elhajlása levezethető a szabadesés egyetemlegességének kiterjesztéséből a fényre, az ilyen számításokból kapott elhajlási szög csak fele az általános relativitáselmélet által megadottnak.

A fény elhajlásához szorosan kapcsolódik a gravitációs időkésleltetés (vagy Shapiro-késleltetés), az a jelenség, hogy a fényjeleknek tovább tart áthaladni egy gravitációs mezőn, mint a mező hiányában. Számos sikeres próbája volt ennek az előrejelzésnek. A paraméteres post-Newton-i formalizmusban (PPN) mind a fény elhajlása, mind a gravitációs időkésleltetés meghatároznak egy γ paramétert, amely kifejezi a gravitáció hatását a tér geometriájára.

Gravitációs hullámok

Egy (linearizált, a jobb láthatóság kedvéért felerősített) gravitációs hullám által torzított kísérleti részecske-gyűrű

Albert Einstein 1916-os előrejelzése alapján léteznek gravitációs hullámok: fodrok a téridő metrikumában, melyek fénysebességgel terjednek. Ezek a gyenge-mezejű gravitáció és az elektromágnesesség közti számos hasonlóság egyike, abban az értelemben, hogy hasonlatosak az elektromágneses hullámokhoz. 2016. február 11-én a LIGO csapata bejelentette, hogy egy kettős fekete lyuk összeolvadása során keletkező gravitációs hullámokat érzékelt közvetlenül.

Egy ilyen hullám legegyszerűbb típusa szemléltethető egy szabadon lebegő részecskékből álló gyűrűn. Egy ilyen gyűrűn, az olvasó felé áthaladó szinuszhullám jellegzetes, ritmikus módon eltorzítja a gyűrűt (animációs képe a jobb oldalon). Mivel az Einstein-féle egyenletek nemlineárisak, a tetszőleges erős gravitációs hullámok nem követik a lineáris szuperpozíciót, megnehezítve leírásukat. Gyenge mezők esetén azonban lehetséges a lineáris közelítés. Az ilyen linearizált gravitációs hullámok elegendően pontosak a nagyon távoli kozmikus események Földre érkező, egyre gyengülő hullámainak leírására, amelyek jellemzően $10^{-21}$-nel vagy még kisebb értékkel növekvő vagy csökkenő relatív távolságokat eredményeznek. Az adatelemzési módszerek rutinszerűen használják azt a tényt, hogy ezek a linearizált hullámok Fourier-felbonthatók.

Vannak egzakt megoldások, amelyek a gravitációs hullámokat bármely közelítés nélkül írják le, pl. az üres térben haladó hullámsorozat vagy az ún. Gowdy-világegyetemek, a gravitációs hullámokkal teli táguló kozmosz változatai. De az asztrofizikailag jelentős szituációk során keletkező gravitációs hullámok esetén, mint pl. két fekete lyuk összeolvadása, jelenleg csak a numerikus módszerek az egyetlen lehetőség a megfelelő modellek megalkotására.

Keringési hatások és az irány relativitása

Az általános relativitáselmélet a klasszikus mechanikától a keringő testek kapcsán számos előrejelzéseben különbözik. Előrejelzi a bolygópályák általános forgási precesszióját, éppúgy mint a gravitációs hullámok kibocsátása és az irány relativitásának hatásai okozta pályasugár-csökkenést.

Az apszispontok precessziója

Egy csillag körül keringő magányos bolygó newtoni (piros) és einsteini (kék) pályája

Az általános relativitáselméletben bármely pálya apszispontja (a rendszer tömegközéppontjához való legközelebb kerülés pontja) el fog mozdulni – a pálya nem egy ellipszis, hanem hasonlatos egy rózsa alakú görbét rajzoló, fókusza körül forgó ellipszishez (ld. az ábrán). Einstein ezt az eredményt először egy newtoni határértéket képviselő közelítő metrika felhasználásával és a keringő testet kísérleti részecskének véve vezette le. Számára az a tény, hogy elmélete egyszerű magyarázatot adott a Merkúr, Urbain Le Verrier által 1859-ben felfedezett anomáliás perihélium eltolódására, fontos bizonyíték volt arra, hogy beazonosította a gravitációs mezőegyenletek helyes alakját.

A hatás szintúgy levezethető vagy ez egzakt (a gömbszerű tömeg körüli téridőt leíró) Schwarzschild-metrika használatával, vagy a sokkal általánosabb post-Newton-i formalizmussal. Ennek oka a gravitáció befolyása a tér geometriájára és a sajátenergia hozzájárulása a test gravitációjához (ami az Einstein-egyenletek nemlinearitásából eredeztethető). A relativisztikus precesszió valamennyi bolygónál megfigyelhető, amelyeknél lehetséges a pontos precessziómérés (Merkúr, Vénusz és a Föld), hasonlóan a kettőspulzár rendszereknél, ahol ez öt nagyságrenddel nagyobb.

Az általános relativitáselméletbe a perihélium σ eltolódása, forgásonkénti radiánban kifejezve, megközelítőleg így adható meg:

$\sigma ={\frac {24\pi ^{3}L^{2}}{T^{2}c^{2}(1-e^{2})}}\ ,$

ahol

• $L$ a fél nagytengely
• $T$ a keringési idő
• $c$ a fénysebesség
• $e$ az excentricitás.

Pályasugár-csökkenés

A PSR1913+16 pályasugár-csökkenése: az időeltolódás másodpercekben három évtizedig követve.

Az általános relativitáselmélet alapján egy kettős rendszer gravitációs hullámokat fog kibocsátani, ezáltal energiát veszít. Emiatt a veszteség miatt a két keringő test közti távolság csökken, és ugyanígy csökken a keringési periódusuk. A Naprendszerben vagy hagyományos kettőscsillag esetén a hatás túl kicsi ahhoz, hogy megfigyelhető legyen. Nem ez a helyzet azonban majdnem kettőspulzárok, két keringő neutroncsillagból álló rendszer esetén, ahol egyikük egy pulzár. A földi megfigyelők szabályos rádióimpulzus-sorozatokat észlelnek, amelyek nagyon pontos óraként szolgálhatnak. Ez teszi lehetővé a keringési periódus mérését. Mivel a neutroncsillagok végtelenül tömörek, az energia jelentős mennyisége gravitációs sugárzás formájában kerül kibocsátásra.

A gravitációs hullámok kibocsátása általi keringési perióduscsökkenést elsőként Hulse és Taylor figyelte meg az általuk 1974-ben felfedezett PSR1913+16 kettőspulzár segítségével. Ez volt a gravitációs hullámok első érzékelése, még ha közvetett módon is, amelyért 1993-ban megkapták a fizikai Nobel-díjat. Azóta több más kettőspulzárt találtak, kiemelkedő a PSR J0737-3039, amelyben mindkét csillag pulzár.

Geodetikus precesszió és tércsavarodás

Számos relativisztikus hatás az irány relativitásával van közvetlen kapcsolatban. Az egyik a geodetikus precesszió: egy giroszkóp tengelyének iránya görbült téridőben való szabadesésben változni fog például a távoli csillagokból érkező fény irányához képest-még ha egy ilyen giroszkóp a lehető legstabilabb iránytartás módját jelenti is („párhuzamos transzport”). A Hold-Föld rendszer estén ezt a hatást a lézeres holdtávolság-mérés segítségével sikerült megmérni. Újabban a Gravity Probe B műhold fedélzetén található kísérleti tömegek esetén mérték meg 0,3%-nál is jobb pontossággal.

Egy forgó tömeg közelében fellép az ún. gravitomagnetikus vagy felcsavarodási hatás. Egy távoli megfigyelő úgy fogja érzékelni, hogy a tömeghez közeli objektumok „felcsavarodnak”. A legextrémebb módon a forgó fekete lyukak esetén, amikor bármely objektum számára, amely az ergoszféraként ismert övezetbe való belépéskor a forgás elkerülhetetlen. Ezeket a hatásokat szintén a szabadesésben levő giroszkóp irányára való befolyásukon keresztül lehet vizsgálni. Némiképp ellentmondásos vizsgálatokat végeztek a LAGEOS műholdak felhasználásával, megerősítve a relativisztikus előrejelzést. A Mars Global Surveyor is felhasználásra került a Mars körül.

Asztrofizikai alkalmazásai

Gravitációs lencse

Einstein-kereszt: ugyanazon csillagászati objektum négy képe egy gravitációs lencse által képezve

A gravitáció általi fényelhajlás a csillagászati jelenségek egy új osztályáért felelős. Ha a csillagász és a távoli célobjektum között egy megfelelő tömeggel és relatív távolságokkal rendelkező masszív objektum található, a csillagász a cél több torzult képét látja majd. Ez a hatás a gravitációs lencse néven ismert. Az összeállítástól, léptéktől és a tömeg eloszlásától függően két vagy több kép, Einstein-gyűrűként ismert fényes gyűrű vagy ívekként ismert részleges gyűrűk létezhetnek. A legkorábbi példát erre 1979-ben fedezték fel; azóta több száz gravitációs lencsét sikerült megfigyelni. Még ha a több kép túl közel is van egymáshoz ahhoz, hogy megkülönböztethető legyen, a hatás mégis mérhető, pl. mint a célobjektum teljes fényesedése; számos ilyen „mikrolencse-eseményt” sikerült megfigyelni.

A gravitációs lencse a megfigyelési csillagászat egy eszközévé fejlődött. Használatos a sötét anyag létezésének és eloszlásának érzékelésére, „természet adta távcsőként” szolgál a távoli galaxisok megfigyelésére, és a Hubble-állandó egy független becslését lehet vele megkapni. A lencsék adatainak statisztikai kiértékelése értékes betekintést ad a galaxisok szerkezeti fejlődésébe.

Gravitációs hullámcsillagászat

Az űrbéli gravitációshullám-érzékelő LISA művészi ábrázolása

A kettőspulzárok megfigyelése erős közvetett bizonyítékot szolgáltat a gravitációs hullámok létezésére (ld. a pályasugár-csökkenést fent). Ezen hullámok érzékelése az aktuális, relativitáshoz kapcsolódó kutatás fő célja. Számos földi gravitációs hullámérzékelő működik jelenleg, legfontosabbak a GEO 600, LIGO (két érzékelő), TAMA 300 és VIRGO interferenciás érzékelők. A különböző pulzáridőzítési hálózatok milliszekundumos pulzárokat használnak a kettős szupermasszív fekete lyukakból származó gravitációs hullámok érzékelésére a 10⁻⁹-10⁻⁶ hertzes frekvenciatartományban. Egy európai űrbéli érzékelő, a eLISA / NGO jelenleg fejlesztés alatt áll, megelőző küldetése LISA Pathfinder 2015 decemberében indult útjára.

A gravitációs hullámok megfigyelése az elektromágneses spektrumbéli megfigyelések kiegészítése miatt ígéretes. További információk begyűjtése várható tőlük a fekete lyukakról és más sűrű objektumokról, mint a neutroncsillagok és fehér törpék, bizonyos típusú szupernóva-berobbanásokról, és a nagyon korai világegyetem folyamatairól, beleértve bizonyos típusú hipotetikus kozmikus húrok nyomait. 2016 februárjában az Advanced LIGO csapata bejelentette, hogy egy fekete lyuk összeolvadásból gravitációs hullámokat érzékeltek.

Fekete lyukak és egyéb tömör objektumok

Amikor egy objektum tömegének a sugarához viszonyított aránya elegendően naggyá válik, az általános relativitáselmélet egy fekete lyuk kialakulását jelzi előre, a tér egy olyan régióját, ahonnan semmi, még a fény sem tud kiszökni. A csillagfejlődés jelenleg elfogadott modelljében az 1,4 naptömegnyi neutroncsillagok, és a néhány és néhány tucat naptömeg közti stelláris fekete lyukakat gondoljuk a nagy tömegű csillagok végső fejlődési állapotának. Általában a galaxisok középpontjában egy pár millió és pár milliárd naptömeg közti nagyon nagy tömegű fekete lyuk található, és úgy gondoljuk, jelenléte fontos szerepet játszott a galaxis és nagyobb kozmikus struktúrák kialakulásában.

Az általános relativitáselmélet egyenletein alapuló szimuláció: egy csillag összeomlása fekete lyuk kialakulásával, miközben gravitációs hullámokat bocsát ki

Csillagászati szempontból a tömör objektumok legfontosabb tulajdonsága, hogy a lehető leghatékonyabb mechanizmussal rendelkeznek a gravitációs energia elektromágneses sugárzássá való átalakítására. Az akkréciót, a por vagy gáznemű anyag stelláris vagy nagyon nagy tömegű fekete lyukakba való behullását tartják felelősnek egyes látványosan fényes csillagászati objektumért, főként galaktikus méretekben változatos fajtájú aktív galaxismagok, és csillagméretű objektumok között a mikrokvazárok esetén. Elsősorban az akkréció vezethet relativisztikus kilövellésekhez, nagy energiájú részecskék fókuszált nyalábaihoz, amelyek az űrbe közel fénysebességgel kerülnek kilövellésre. Az általános relativitáselmélet központi szerepet játszik mindezen jelenségek modellezésében, és a megfigyelések erős bizonyítékokat szolgáltatnak az elmélet által előrejelzett tulajdonságokkal rendelkező fekete lyukak létezésére.

A fekete lyukak is a gravitációs hullámok utáni kutatás keresett célpontjai (ld. Gravitációs hullámok fent). Kettős fekete lyukak összeolvadása eredményezheti az itt, a Földön található érzékelőket elérő legerősebb gravitációs hullámjelek némelyikét, és a közvetlenül az összeolvadás előtti fázis ("chirp") használható standard gyertyaként az összeolvadási esemény távolságának meghatározásához-és ezzel a nagy távolságban végbemenő világegyetem-tágulás vizsgálatául szolgálhat. Egy stelláris fekete lyuk becsapódása egy nagyon nagy tömegűbe közvetlen információkkal szolgálhat a nagyon nagy tömegű fekete lyuk geometriájáról.

Kozmológia

Ez a kék patkó egy távoli galaxis, amely az előtérben levő nagy tömegű fényes vörös galaxis erős gravitációs vonzásának hatására egy közel teljes gyűrűvé erősödött és vetemedett

A kozmológia jelenlegi modelljei az Einstein-féle mezőegyenleteken alapulva tartalmazzák a Λ kozmológiai állandót, mivel ennek fontos befolyása van a kozmosz nagyléptékű dinamikájára,

$R_{\mu \nu }-{\textstyle 1 \over 2}R\,g_{\mu \nu }+\Lambda \ g_{\mu \nu }={\frac {8\pi G}{c^{4}}}\,T_{\mu \nu }$

ahol $g_{\mu \nu }$ a téridő metrikája. Ezen fejlett egyenletek izotróp és homogén megoldása, a Friedmann–Lemaître–Robertson–Walker-megoldás, lehetővé teszi a fizikusok számára egy, az elmúlt 14 milliárd év alatt egy forró, korai ősrobbanás fázisából kifejlődött világegyetem modellezését. Amint egy kis számú paraméter (például a világegyetem átlagos anyagsűrűsége) megfigyelések segítségével rögzítésre került, a további megfigyelési adatok felhasználhatók a modell vizsgálatára. Az előrejelzések mind sikeresen tartalmazzák az legelső nukleoszintézis időszaka során kialakult vegyi elemek kezdeti sokaságát, a világegyetem nagy léptékű szerkezetét, és a korai kozmoszból származó "hőmérsékleti visszhang", a kozmikus háttérsugárzás létezését és tulajdonságait.

A kozmikus tágulás mértékének csillagászati megfigyelései lehetővé teszik a világegyetemben jelen levő anyag teljes mennyiségének a becslését, bár ezen anyag természete részben titokzatos marad. Az összes anyag közel 90%-a ún. sötét anyag lehet, aminek van tömege (vagy ennek megfelelően gravitációs befolyása), de nincs elektromágneses közrehatása, tehát nem lehet közvetlenül érzékelni. Ennek az új fajta anyagnak nincs általánosan elfogadott leírása, az ismert részecskefizika keretein belül, sem másképpen. A távoli szupernóvák vöröseltolódási kutatásainak megfigyelési bizonyítéka és a kozmikus háttérsugárzás mérései szintén azt mutatják, hogy világegyetemünk fejlődését jelentősen befolyásolja a kozmológiai állandó, amely a kozmikus tágulás gyorsulását eredményezi, vagy ezzel egyenértékűen a sötét energiaként ismert, szokatlan állapotegyenletű energiaforma, amelynek a természete tisztázatlan marad.

Egy ún. felfúvódási fázisnak, egy, a kozmikus idő szerinti 10⁻³³ másodperc körüli erősen gyorsuló tágulás újabb fázisának 1980-as elméleti kidolgozásával tették meg ezt felelősnek a számos zavaró megfigyelésért, amelyek magyarázat nélkül maradtak a klasszikus kozmológiai modell által, mint például a kozmikus háttérsugárzás közel tökéletes homogenitása. A kozmikus háttérsugárzás legújabb méréseinek eredménye az első bizonyíték erre a forgatókönyvre. Azonban zavarba ejtően sokféle lehetséges felfúvódási forgatókönyv van, amelyek nem zárhatók ki a jelenlegi megfigyeléseinkkel. Egy még nagyobb kérdés a korai világegyetem fizikája, a felfúvódási fázis előtt és közel ahhoz, ahol a klasszikus modell a nagy bumm szingularitást jelzi előre. Egy hiteles válaszhoz szükség lehet a kvantumgravitáció teljes elméletére, amely még nem került kidolgozásra (vö. a kvantumgravitáció résszel lentebb).

Időutazás

Kurt Gödel megmutatta, hogy léteznek az Einstein-féle egyenleteknek zárt időszerű görbéket (CTC-ket) tartalmazó megoldásai, amelyek lehetővé teszik a hurkokat az időben. A megoldáshoz olyan szélsőséges fizikai feltételek szükségesek, amelyek nem valószínű, hogy a gyakorlatban valaha is előfordulnak, és nyitott kérdés marad, vajon a fizika további törvényei eltörlik-e őket teljesen. Azóta más – hasonlóan nem gyakorlatias – GR-megoldásokat sikerült találni, mint a Tipler-henger és az átjárható féreglyukak.

Továbbfejlesztett elképzelések

Kauzális struktúra és globális geometria

Egy végtelen Minkowski-világegyetem Penrose–Carter diagrammja

Az általános relativitáselméletben semmilyen anyagi test sem közelítheti vagy előzheti meg a fényimpulzust. Egyetlen A esemény befolyása sem érhet el egy másik X helyet az A-ból X-be küldött fény előtt. Következésképp, az összes fény világvonal (nullás geodetikák) felkutatása magában hordozza a téridő kauzális struktúrájának kulcsfontosságú információit. Ez a struktúra ábrázolható Penrose–Carter-diagrammokkal, amelyekben a tér végtelenül nagy régiói és végtelen időintervallumai össze vannak tömörítve ("kompaktifikálva"), hogy ráférjenek egy véges térképre, míg a fény továbbra is az átlók mentén halad, mint a hagyományos téridődiagramokon.

Tudatában a kauzális struktúrák fontosságának, Roger Penrose és mások kifejlesztették a globális geometriát. A globális geometriában a vizsgálat tárgya nem az Einstein-féle egyenletek egy egzakt megoldása (vagy megoldáscsaládja). Ehelyett az összes geodetikára igaz összefüggések, mint a Raychaudhuri-egyenlet, és további nem specifikus feltételezések az anyag természetéről (általában ún. energiafeltételek formájában) használatosak az általános eredmények levezetésére.

Horizontok

A globális geometria használatával egyes téridőkben kimutathatók a horizontoknak nevezett határok, amelyek elválasztanak egy régiót a téridő többi részétől. A legismertebb példák erre a fekete lyukak: ha a tömeg a tér egy elegendően sűrű régiójába tömörödik (ahogy azt a karika-sejtés meghatározza), a megfelelő távolsági tartomány a Schwarzschild-sugár), a fény belülről nem tud kiszökni a külvilágba. Mivel semmilyen objektum sem előzheti meg a fényimpulzust, a belül levő anyag szintén be van zárva. A külvilágból befelé az átjárás továbbra is lehetséges, ami azt mutatja, hogy a határ, a fekete lyuk horizontja nem egy fizikai akadály.

Egy forgó fekete lyuk ergoszférája, ami fontos szerepet játszik egy ilyen fekete lyukból való energiakivételnél

A fekete lyukak korai tanulmányai az Einstein-féle egyenletek egzakt megoldásaira támaszkodtak, mégpedig a gömbszimmetrikus Schwarzschild-megoldásra (ami egy statikus fekete lyuk leírására használatos) és a tengelyszimmetrikus Kerr-megoldásra (ami egy forgó, nyugalmi fekete lyuk leírására használatos), és olyan érdekes jellegzetességeket vezettek be, mint az ergoszféra. A globális geometria használatával a későbbi tanulmányok a fekete lyukak több általános tulajdonságát is felfedték. Hosszútávon inkább egyszerű objektumok, ahol tizenegy paraméter határozza meg az energiát, a lendületet, a perdületet, a helyzetet egy adott időben és az elektromos töltést. Ezt állítja a fekete lyuk egyediségi tétel: "a fekete lyukak kopaszak", azaz nincsenek az emberi frizurákhoz hasonló megkülönböztető jegyeik. Tekintet nélkül a fekete lyukká alakuló összezuhanó gravitációs objektum bonyolultságára, az eredményobjektum (gravitációs hullámok kibocsátásával) nagyon egyszerű.

Ennél is figyelemre méltóbb, hogy létezik olyan, fekete lyuk mechanikája néven ismert általános törvényösszesség, amely hasonlatos a termodinamika törvényeihez. Például a fekete lyuk mechanikájának második törvénye alapján egy általános fekete lyuk eseményhorizontjának a területe nem fog csökkenni az idővel, hasonlóan a termodinamikai rendszer entrópiájához. Ez behatárolja azt az energiát, ami egy forgó fekete lyukból klasszikus módszerekkel kivonható (pl. a Penrose-folyamat által). Erős bizonyíték van arra, hogy a fekete lyuk mechanikájának törvényei valójában a termodinamikai törvények alkészlete, és a fekete lyuk területe arányos az entrópiájával. Ez a fekete lyuk mechanikájának eredeti törvényeit módosítja: például úgy, hogy a fekete lyuk mechanikájának második törvénye a termodinamika második törvényének a része lesz, lehetséges a fekete lyuk területének csökkennie – amennyiben más folyamatok biztosítják, hogy összességében az entrópia növekszik. Épp úgy mint a nem nulla hőmérsékletű termodinamikai objektumoknak, a fekete lyukaknak is hőmérsékleti sugárzást kell kibocsátaniuk. A félklasszikus számítások azt mutatják, hogy tényleg így van, ahol a felületi gravitáció szerepel a hőmérséklet helyén Planck törvényében. Ez a sugárzás Hawking-sugárzásként ismert (vö. a kvantumelmélet résszel, lentebb).

Vannak más típusú horizontok is. Egy táguló világegyetemben egy megfigyelő úgy találhatja, hogy a múlt néhány régiója nem megfigyelhető ("részecskehorizont"), és a jövő néhány régiója nem befolyásolható (eseményhorizont). Még a lapos Minkowski-térben is, egy gyorsuló megfigyelő által leírva (Rindler-tér), lesznek az Unruh-sugárzás néven ismert félklasszikus sugárzáshoz társítható horizontok.

Evolúciós egyenletek

Az Einstein-féle egyenletek minden egyes megoldása lefedi a világegyetem teljes történelmét – nemcsak valamiféle pillanatkép a dolgok állásáról, hanem egy teljes, vélhetően anyaggal teli téridő. Az adott világyegyetemben leírja az anyag állapotát és geometriáját mindenhol és minden időpillanatban. Általános kovarianciája okán Einstein elmélete önmagában nem elegendő a metrika tenzor időbeli fejlődésének meghatározására. Vegyíteni kell egy koordinátafeltétellel, ami hasonlatos a más mezőelméletekbeli mértékszabadsággal.

Ahhoz, hogy az Einstein-féle egyenleteket parciális differenciálegyenletekként megértsük, segítség lehet olyan formában kifejezni őket, ami a világyegyetem fejlődését írja le az időben. Ez az ún. „3+1” alakban lehetséges, ahol a téridő három térbeli és egy időbeli dimenzióra bomlik. A legismertebb példa erre az ADM formalizmus. Ezek a felbontások megmutatják, hogy az általános relativitáselmélet téridő fejlődési egyenletei jól viselkednek: a megoldások mindig léteznek, és egyedileg meghatározottak, miután a megfelelő kezdeti feltételek megadásra kerültek. Az Einstein-féle mezőegyenletek ilyen alakjai a numerikus relativitáselmélet alapjai.

Globális és kvázi-globális mennyiségek

A fejlődési egyenletek elképzelése szorosan kapcsolódik az általános relativitáselmélet fizikájának egy másik szemszögéhez. Einstein elméletében úgy tűnik, lehetetlen általános meghatározását találni egy olyan, látszólag egyszerű tulajdonságnak, mint egy rendszer teljes tömege (vagy energiája). A fő ok, hogy a gravitációs mezőnek – mint minden más fizikai mezőnek – egy bizonyos energiát kell tulajdonítani, de alapvetően lehetetlennek tűnik ezen energia helyének a meghatározása.

Mindazonáltal vannak lehetőségek egy rendszer teljes tömegének a meghatározására, vagy a hipotetikus „végtelen távoli megfigyelő” (ADM-tömeg), vagy megfelelő szimmetriák (Komar-tömeg) használatával. Ha kivesszük a rendszer teljes tömegéből a gravitációs hullámok által a végtelenben elvitt energiát, az eredmény az ún. Bondi-tömeg a nullás végtelenben. Mint ahogy a klasszikus fizikában is, megmutatható, hogy ezek a tömegek pozitívak. Megfelelő globális meghatározások léteznek a lendületre és a perdületre. Számos próbálkozás volt már a kvázi-globális mennyiségek meghatározására, mint például egy elszigetelt rendszer tömege, csak az ezt a rendszert tartalmazó tér egy véges régiójában meghatározott mennyiségeinek használatával. Remélhetően megkapunk egy mennyiséget, amely elszigetelt rendszerekről szóló általános állításokra alkalmas, mint a karika-sejtés pontosabb kifejezése.

Viszonya a kvantumelmélettel

Ha az általános relativitáselméletet tekintjük a modern fizika egyik tartópillérének, akkor a kvantumelmélet, az elemi részecskéktől a szilárdtestfizikáig terjedő anyag megértésének az alapja, lenne a másik. A kvantumelmélet összeegyeztetése az általános relativitáselmélettel azonban még nyitott kérdés.

Kvantum mezőelmélet a görbült téridőben

A hagyományos kvantum mezőelméletek, amelyek a modern elemi részecskefizika alapját képezik, a lapos Minkowski-térben vannak meghatározva, amely egy nagyszerű közelítés, amikor a makroszkopikus részecskék olyan gyenge gravitációs mezőben való viselkedésének a leírásáról van szó, mint ami a Földön található. Ahhoz, hogy leírjuk azokat a helyzeteket, ahol a gravitáció elég erős a (kvantum) anyag befolyásolására, mégsem akkora, hogy önmaga kvantizációjára lenne szükség, a fizikusok kialakították a kvantum mezőelméleteket a görbült téridőben. Ezek az elméletek az általános relativitáselméletre támaszkodnak a görbült háttér téridő leírásához, és meghatároznak egy általánosított kvantum mezőelméletet a kvantum anyagnak ebben a téridőben való viselkedésére. Ennek a formalizmusnak a felhasználásával megmutatható, hogy a fekete lyukak részecskék Hawking-sugárzásként ismert feketetest spektrumát bocsátják ki, azt a lehetőséget vonva maguk után, hogy idővel elpárolognak. Ahogy fentebb röviden megemlítettük, ez a sugárzás fontos szerepet játszik a fekete lyukak termodinamikájában.

Kvantumgravitáció

Az anyag kvantumleírása és a téridő geometriai leírása közti konzisztencia iránti igény, valamint a szingularitások felbukkanása (ahol a görbület hosszléptékei mikroszkopikussá válnak), jelzik a kvantumgravitáció teljes elméletének a szükségességét: a fekete lyukak belsejének és a nagyon korai világegyetemnek a megfelelő leírásához egy olyan elmélet szükséges, amelyben a gravitáció és a téridő társult geometriája a kvantumfizika nyelvén van leírva. A jelentős erőfeszítések ellenére jelenleg nem ismert a kvantumgravitáció teljes és konzisztens elmélete, bár számos ígéretes jelölt akad.

Egy Calabi–Yau-sokaság kivetítése, egyik módja a húrelmélet által rögzített extra dimenziók tömörítésének

Az elemi részecskefizikában az alapvető kölcsönhatások leírására használt hagyományos kvantum mezőelméletek általánosítására tett próbálkozások, úgy mint a gravitáció belefoglalása, komoly problémákhoz vezettek. Egyesek azzal érveltek, hogy alacsony energiáknál ez a megközelítés sikeresnek bizonyul abban a tekintetben, hogy a gravitáció egy elfogadható effektív (kvantum) mezőelméletét eredményezi. Nagyon nagy energiák esetén azonban a perturbáló eredmények súlyosan divergensek, és az előrejelző erejüktől mentes modellekhez vezetnek ("perturbáló nem-renormalizáció").

A hurok-kvantumgravitációban használt típusú egyszerű spinhálózat

Ezen korlátokon való felülemelkedés egyik próbálkozása a húrelmélet, amely nem pontrészecskék elmélete, hanem pillanatnyi, egy dimenziós kiterjedésű objektumoknak. Az elmélet minden részecske és kölcsönhatás, beleértve a gravitáció egységes leírásának ígérkezik; ennek az ára olyan szokatlan jellegzetességek, mint a tér a szokásos hármon felüli hat extra dimenziója. Az ún második szuperhúr-forradalomban úgy sejtették, hogy mind a húrelmélet, mind az általános relativitáselmélet és a szuperszimmetria szupergravitáció néven ismert egyesítése az M-elmélet néven ismert hipotetikus tizenegy dimenziós modell részét képezik, amely megalapozná kvantumgravitáció egységesen meghatározott és konzisztens elméletét.

Egy másik megközelítés a kvantumelmélet kanonikus kvantizációs eljárásaival kezdődik. Az általános relativitáselmélet kezdeti érték kialakulásának használatával (vö. evolúciós egyenletek fent) az eredmény a Wheeler-deWitt-egyenlet (hasonlatos a Schrödinger-egyenlethez), amely sajnálatos módon rosszul meghatározottá válik a megfelelő ibolyántúli rács levágása nélkül. Azonban annak bevezetése, amit manapság Ashtekar-változókként ismerünk, a hurok-kvantumgravitáció ígéretes modelljéhez vezet. A teret egy spinhálózatnak nevezett hálószerű struktúra képviseli, amely az időben diszkrét lépésekkel fejlődik.

Attól függően, hogy az általános relativitáselmélet és a kvantumelmélet melyik tulajdonságát fogadjuk el változatlannak, és milyen szinten kerülnek bevezetésre változások, számos egyéb próbálkozás is létezik egy életképes kvantumgravitáció elérésére, ennek egyes példái a Feynman útintegrál-megközelítésén és a Regge-számtanon alapuló gravitációs rácselmélet, a dinamikus háromszögesítések, a kauzális készletek, a twistor-modellek vagy a kvantumkozmológia útintegrál-alapú modelljei.

Az összes elméletjelöltnek vannak megoldandó jelentős formális és elképzelésbeli problémái. Szembesülnek azzal a közös problémával is, hogy még nincs módszer arra, hogy a kvantumelmélet előrejelzéseit kísérleti vizsgálatokba ültessük át (és ezzel eldöntsük a jelöltek között, hol különböznek az előrejelzéseik), habár van remény ennek megváltozására, amint a világegyetembeli megfigyelések és részecskefizikai kísérletek jövőbeli adatai elérhetővé válnak.

Jelenlegi állapot

A GW150914 kettős fekete lyuk összeolvadásából keletkező gravitációs hullámok megfigyelése.

Az általános relativitáselmélet mint a gravitáció és a kozmológia nagyon sikeres modellje jelent meg, amely sikeresen teljesített sok egyértelmű megfigyelésben és kísérleti vizsgálatban. Azonban erős jelei mutatkoznak, hogy az elmélet nem teljes. A kvantumgravitáció problémája és a téridő szingularitások valóságának kérdése nyitott marad. A sötét energia és a sötét anyag bizonyítékának tekintett megfigyelési adatok azt jelezhetik, hogy egy új fizikára lehet szükség. Önmagában véve is az általános relativitáselmélet gazdag a további kutatásra érdemes lehetőségekben. A matematikus relativisták a szingularitások természetének és az Einstein-féle egyenletek alapvető tulajdonságainak a megértését keresik, míg a numerikus relativisták egyre erősebb számítógépes szimulációkat (mint például az egyesülő fekete lyukakat leírót) futtatnak. 2016 februárjában bejelentették, hogy a gravitációs hullámok létezését az Advanced LIGO csapat 2015. szeptember 14.-én közvetlenül is érzékelte. Bevezetése után egy évszázaddal az általános relativitáselmélet egy nagyon aktívan kutatott terület marad.

Kapcsolódó szócikkek

• Alcubierre-meghajtás (warp meghajtás)
• Relativitáselmélet
• Gravitációs lencse
• Gravitációs mikrolencse
• Arthur Stanley Eddington
• Albert Einstein

Irodalom

Magyar nyelvű könyvek

• Landau – Lifsic: Elméleti fizika II. Tankönyvkiadó, Budapest, 1976
• Novobátzky Károly: A relativitás elmélete. Tankönyvkiadó, Budapest, 1963
• Perjés Zoltán: Általános relativitáselmélet. Akadémiai Kiadó. Budapest. 2006. ISBN 963-05-8423-9

Népszerű könyvek

• Geroch, R. (1981), General Relativity from A to B, Chicago: University of Chicago Press, ISBN 0-226-28864-1
• Lieber, Lillian (2008), The Einstein Theory of Relativity: A Trip to the Fourth Dimension, Philadelphia: Paul Dry Books, Inc., ISBN 978-1-58988-044-3
• Wald, Robert M. (1992), Space, Time, and Gravity: the Theory of the Big Bang and Black Holes, Chicago: University of Chicago Press, ISBN 0-226-87029-4
• Wheeler, John & Ford, Kenneth (1998), Geons, Black Holes, & Quantum Foam: a life in physics, New York: W. W. Norton, ISBN 0-393-31991-1

Kezdő szintű egyetemi tankönyvek

• Callahan, James J. (2000), The Geometry of Spacetime: an Introduction to Special and General Relativity, New York: Springer, ISBN 0-387-98641-3
• Taylor, Edwin F.; Wheeler, John Archibald (2000), Exploring Black Holes: Introduction to General Relativity, Addison Wesley, ISBN 0-201-38423-X

Haladó szintű egyetemi tankönyvek

• B. F. Schutz (2009), A First Course in General Relativity (Second Edition), Cambridge University Press, ISBN 978-0-521-88705-2
• Cheng, Ta-Pei (2005), Relativity, Gravitation and Cosmology: a Basic Introduction, Oxford and New York: Oxford University Press, ISBN 0-19-852957-0
• Gron, O. & Hervik, S. (2007), Einstein's General theory of Relativity, Springer, ISBN 978-0-387-69199-2
• Hartle, James B. (2003), Gravity: an Introduction to Einstein's General Relativity, San Francisco: Addison-Wesley, ISBN 0-8053-8662-9
• Hughston, L. P. & Tod, K. P. (1991), Introduction to General Relativity, Cambridge: Cambridge University Press, ISBN 0-521-33943-X
• d'Inverno, Ray (1992), Introducing Einstein's Relativity, Oxford: Oxford University Press, ISBN 0-19-859686-3
• Ludyk, Günter. Einstein in Matrix Form, 1st, Berlin: Springer (2013. december 29.). ISBN 978-3-642-35797-8 

Doktori szintű tankönyvek

• Carroll, Sean M. (2004), Spacetime and Geometry: An Introduction to General Relativity, San Francisco: Addison-Wesley, ISBN 0-8053-8732-3
• Grøn, Øyvind & Hervik, Sigbjørn (2007), Einstein's General Theory of Relativity, New York: Springer, ISBN 978-0-387-69199-2
• Landau, Lev D. & Lifshitz, Evgeny F. (1980), The Classical Theory of Fields (4th ed.), London: Butterworth-Heinemann, ISBN 0-7506-2768-9
• Misner, Charles W.; Thorne, Kip. S. & Wheeler, John A. (1973), Gravitation, W. H. Freeman, ISBN 0-7167-0344-0
• Stephani, Hans (1990), General Relativity: An Introduction to the Theory of the Gravitational Field,, Cambridge: Cambridge University Press, ISBN 0-521-37941-5
• Wald, Robert M. (1984), General Relativity, University of Chicago Press, ISBN 0-226-87033-2

További információk

A Wikimédia Commons tartalmaz Általános relativitáselmélet témájú médiaállományokat.

Az angol Wikikönyvekben
további információk találhatók

Általános relativitáselmélet témában.

A magyar Wikiforrásban további forrásszövegek találhatóak

Relativitás témában.

A magyar Wikiforrásban további forrásszövegek találhatóak

Relativitás: A speciális és általános elmélet témában.

• Einstein Online – Az átlag olvasó számára érthető cikkek a relativisztikus fizika különböző aspektusairól, a Max Planck Gravitációsfizikai Intézet gondozásában
• NCSA Spacetime Wrinkles – készítette a NCSA numerikus relativitás csoportja, egy alapszintú bevezetéssel az általános relativitáselméletbe

• Kurzusok
• Előadások
• Segédletek

• Einstein's General Theory of Relativity. YouTube (Leonard Susskind előadása 2008. szeptember 22-én a Stanford Egyetemen).
• Általános relativitáselméleti előadások sorozata elhangzott 2006-ban a Henri Poincaré Intézetben (kezdő/haladó).
• Általános relativitáselméleti segédletek John Baez-től.
• Brown, Kevin: Reflections on relativity. Mathpages.com. [2015. december 18-i dátummal az eredetiből archiválva]. (Hozzáférés: 2005. május 29.)
• Carroll, Sean M.: Lecture Notes on General Relativity. (Hozzáférés: 2014. január 5.)
• Moor, Rafi: Understanding General Relativity. [2015. december 28-i dátummal az eredetiből archiválva]. (Hozzáférés: 2006. július 11.)
• Waner, Stefan: Introduction to Differential Geometry and General Relativity (PDF). [2015. április 19-i dátummal az eredetiből archiválva]. (Hozzáférés: 2015. április 5.)

Fordítás

Ez a szócikk részben vagy egészben a General relativity című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.