Húrelmélet

Az anyag különböző szinteken, egészen a feltételezett húrok szintjéig.
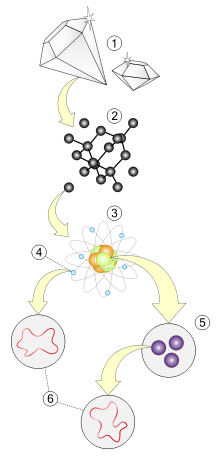
Magyarázat 1 Anyag, 2 Molekulaszerkezet (atomok), 3 Atom (proton, neutron, elektron), 4 Elektron, 5 Kvark, 6 Húr

A húrelmélet és az M-elmélet két egymásra épülő részecskefizikai modell, mely a részecskéket nem pontszerű, hanem kiterjedt objektumokként kezeli (húrok, membránok). A húrelméletnek a szuperszimmetriát is tartalmazó változatát gyakran szuperhúrelméletnek nevezik. Ezeket az elméleteket azért hozták létre, hogy az általános relativitáselméletet és a kvantummechanikát összhangba hozzák, és elkerüljék a részecskefizikának azokat a buktatóit, melyek a pontszerű részecskék feltételezésével előbukkannak. Az M-elméletben nemcsak húrokat, hanem membránokat és magasabb dimenziós objektumokat is feltételeznek. Jelenleg nincs semmilyen kísérleti tény, amely a húrelméletet igazolná vagy cáfolná.

A húrelmélet elnevezést mind a 26 dimenziós bozonikus húrelméletekre, mind a szuperszimmetria felfedezése után annak hozzáadásával nyert szuperhúrelméletre szokták használni. Újabban gyakran a szuperhúrelméletet mondjuk húrelméletnek. Az 1990-es években Edward Witten és mások meggyőző bizonyítékokat találtak arra, hogy a különböző szuperhúr elméletek (öt különböző változata van) egy M-elméletnek nevezett 11 dimenziós elmélet határesetei. Ezzel indult el a második szuperhúr-forradalom. (Az M-elméletnek még a fekete lyukak termodinamikájában is sikerült olyan eredményeket elérnie, amelyek a korábbi számításokkal összhangban vannak.)

A húrelmélet főként annak köszönheti népszerűségét, hogy reményeink szerint képes az összes erőhatás leírását egyetlen elméletbe összesűríteni. A húrelméletnek köszönhető, hogy mélyebben sikerült megértenünk a szuperszimmetrikus térelméleteket, amelyek a részecskéket pontszerűnek tekintő standard modellnek lehetséges kiterjesztései.

Extra dimenziók

A húrelmélet egyik furcsa tulajdonsága, hogy feltételezi, hogy az univerzumnak sok dimenziója van, és megjósolja a számukat. Sem Maxwell elmélete az elektromágnességről, sem Einstein relativitáselmélete nem adja meg a dimenziószámot. A jól ismert 3 tér és egy idődimenziót "kézzel" helyezzük bele ezekbe az elméletekbe. Ezzel szemben a húrelméletben megjósolható a téridő dimenziószáma alapvető elvekből. (Adott dimenziószám szükséges ahhoz, hogy az elmélet Lorentz-invariáns legyen.) Az egyetlen probléma, hogy ha kiszámoljuk a szükséges dimenziószámot, akkor nem négyet (3 tér + 1 idő), hanem 26-ot, 10-et, illetve 11-et kapunk a bozonikus húrelméletben, a szuperhúrelméletben, illetve az M-elméletben.

Világvonalak és világfelületek

Ezek a tények komolyan ellentmondanak a megfigyelt eseményeknek. A fizikusok a következő két lehetőség egyikével oldják meg a problémát. Az első módszer, ha összezsugorítjuk a hiányzó dimenziókat. Ez azt jelenti, hogy a 6 vagy 7 dimenzió olyan kicsi, hogy nem észlelhető a kísérleteinkben. A 6 dimenziós esetben ezt a Calabi–Yau-terekkel oldják meg. 7 dimenzióban úgynevezett G₂ manifoldokkal. Lényegében a hiányzó dimenziókat úgy teszik kicsivé, hogy azok magukba hurkolódnak. A szokásos hasonlat erre a locsolócső. Távolról nézve egydimenziós alakzatnak, vonalnak látszik, de ha közelebb megyünk, láthatóvá válik a második kiterjedése, amely kör keresztmetszetű. Ehhez hasonlóan úgy gondoljuk, hogy a hiányzó dimenziók csak közelről nézve láthatóak.

(Természetesen a locsolócső 3 dimenziós, de mi csak a felületén mozgunk. Ekkor a helyünket két számmal adhatjuk meg. Az egyik kitüntetett végétől való távolsággal és kerületén például a felső ponttól egyik kitüntetett körüljárási irányban mért távolsággal. Mivel a hely megadásához két adat kell és elegendő, ezért mondjuk, hogy a locsolócső felszíne kétdimenziós. A földfelszín is kétdimenziós, hiszen a földrajzi szélesség és hosszúság (két adat) ismeretében a hely adott.)

A másik lehetőség az, hogy mi a világegyetemnek egy 3+1 dimenziós alterében élünk, ahol a +1 emlékeztet arra, hogy az idő egy másfajta dimenzió, mint a tér. Mivel ez a látásmód D-brán nevű matematikai objektumokkal írja le elméletét, ezért ezt bránvilág elméletnek nevezzük. Egy érdekes mellékterméke, hogy eszerint elképzelhető, hogy a kvantumgravitációs jelenségeket akár a CERN 2008-ban elindult gyorsítógyűrűjében, a Nagy Hadronütköztetőben (LHC) megfigyeljünk. Bár ez érdekes dolog, ebben a lehetőségben azért nem sokan hisznek.

A relativitáselmélet és a kvantummechanika egyesítése

A húrelmélet 3 dolgot tud magyarázni: alapvető kölcsönhatások, a gravitáció gyengesége, a részecskék tulajdonságai.

Ami a kölcsönhatásokat illeti az erős kölcsönhatást, a gyenge kölcsönhatást és az elektromágneses kölcsönhatást nyitott húrok közvetítik amelyek csak a három dimenziós térben képesek mozogni ámde a gravitációt ha úgy fogjuk fel mint Einstein tehát a tér görbületeként akkor meggörbíti a tömeg a többi irányban is a teret és ezért észleljük gyengének a többi kölcsönhatáshoz képest ha részecskeként képzeljük el akkor a gravitonok képesek a többi dimenzióban is mozogni mert ezeket zárt húrok alkotják és valamivel kisebb mint a többi részecske mert valamiért a graviton húrjai sokkal kisebbre vannak formálva és de ez lehetőséget ad neki mozogni a többi irányba, egyébként a sötét energia is valahogy így működik hogy az összes dimenzióban hat és több dimenzió azt is magyarázza hogy mért viselkednek az alapvető részecskék olyan furán valamint a sötét anyagot úgy magyarázná hogy annak nincs kiterjedése a 3 dimenziós térben ezért csak a gravitációs hatását észleljük.

Problémák a húrelmélettel

A húrelméletnek három komolyabb problémája van. Az első, hogy senki sem képes megoldani a húrok mezőelméletét, vagy hogy bármilyen más nemperturbatív eredményt hozzon ki a húrelméletből. A feladat kristálytiszta, de a sors iróniája, hogy a megoldása olyan technikákat igényel, amelyek túlmutatnak a fizikusok jelenlegi képességein. Érdekes tény, hogy miközben a huszonegyedik század fizikája véletlenül belepottyant a huszadik századba, a huszonegyedik század matematikája még nem született meg; s már csak ezért is él ez a probléma, hogy a jelenben e húrok mezőelméletét nem tudjuk megoldani.

A második, hogy a 10⁻³⁵ méter átmérőjű húrokat jelenlegi technikánkkal képtelenek vagyunk megfigyelni.

A harmadik probléma az, hogy a kvantumtérelmélethez hasonlóan csak perturbatívan kezelhető (közelítések sorozatával pontos megoldás helyett). Bár komoly előrelépések történtek a nemperturbatív módszerek felé, a teljes elmélet nem írható le ily módon.

A húrelmélet típusai

Öt különböző típusú húrelmélet létezik. Ezek a következőek: I típus, IIA típus, IIB típus, heterotikus-O és heterotikus-E. Ezekről sokáig azt hitték, hogy különbözőek, de a közelmúltban kiderült, hogy a húrelméletek között van összefüggés. Mert ha figyelembe vesszük a dualitást, akkor a csatolási állandók változtatása az egyik típustól elvisz a másik típusig. Így az I típusú duális a heterotikus-O-val, a heterotikus-E a IIA típusúval egyesül az M-elméleten belül, a IIB típusú pedig önmagával duális. Valamint ha figyelembe vesszük a téridő geometria dualitását is, akkor a heterotikus-O duális a heterotikus-E-vel, valamint a IIA típusú a IIB típusúval.

I típus <---> heterotikus-O

IIA típus <---> heterotikus-E

IIB típus <---> IIB típus

heterotikus-O <...> heterotikus-E

IIA típus <...> IIB típus

Források

• Csaba, Zoltán (2005). „Szuperhúrok és a mindenség eredete”. Új Galaxis. Tudományos-fantasztikus antológia, Pécs 5, 116–148. o, Kiadó: Kódex Kiadó. 
• Jéki, László: Szuper szuperhúrok. [2005. március 16-i dátummal az eredetiből archiválva]. (Hozzáférés: 2005. március 10.)
• The Official String Theory Web Site (angol nyelven)

További információk

• Györfi András: Kalandos fizika. Egy viking portya története a húrelmélet és kozmológia felségvizein; Pallas-Akadémia, Csíkszereda, 2010
• Lee Smolin: Mi a gubanc a fizikával? A húrelmélet problémái és a lehetséges kiutak; ford. Koronczay Dávid; Akkord, Bp., 2011 (Talentum tudományos könyvtár)