Gravitációs idődilatáció

A gravitációs idődilatáció az időeltolódás egy fajtája, amely jelenség a különböző, egymáshoz képest gyorsuló vonatkoztatási rendszerekben történő megfigyelések során lép fel. Két esemény között eltelt idő tényleges különbsége, amelyet a gravitációs tömegtől különböző távolságban lévő megfigyelők mérnek. Minél alacsonyabb a gravitációs potenciál (minél közelebb van az óra a gravitáció forrásához), annál lassabban telik az idő, és ellenkezőleg gyorsabban, ahogy a gravitációs potenciál növekszik (az óra eltávolodik a gravitációs forrástól). Albert Einstein eredetileg relativitáselméletében jósolta ezt a hatást, és ezt azóta az általános relativitáselméleti tesztek is megerősítették.^[1]

Ez bebizonyította, hogy az eltérő magasságban lévő atomórák (és így a különböző gravitációs potenciálon) végül különböző időket mutatnak. Az ilyen földhöz kötött kísérletek során kimutatott hatások rendkívül kismértékűek, a különbségeket nanoszekundumokban mérik. A Föld évmilliárdos korához viszonyítva, a Föld magja gyakorlatilag csak 2,5 évvel fiatalabb a felszínénél.^[2] A nagyobb hatások szemléltetéséhez nagyobb távolságokra lenne szükség a Földtől vagy egy másik, nagyobb gravitációs forrásra.

A gravitációs időeltolódást Albert Einstein írta le először 1907-ben,^[3] mint a speciális relativitáselmélet következményét a gyorsuló vonatkoztatási rendszerekben. Az általános relativitáselméletben, a különböző pozíciókban vett sajátidők közötti időbeli különbségének tekinthető, amelyet a téridő metrikus tenzora ír le. A gravitációs időeltolódás meglétét először közvetlenül Pound – Rebka kísérlettel erősítették meg 1959-ben, később pedig a Gravity Probe A és más kísérletek precízebben alátámasztották az eredményeket.

Meghatározás

A nagy tömegű testektől távol eső (vagy nagyobb gravitációs potenciállal rendelkező) órák gyorsabban járnak, míg a masszív testekhez közeli (vagy alacsonyabb gravitációs potenciállal rendelkező) órák pedig lassabban járnak. Például a Föld teljes időtartamát (4,6 milliárd év) figyelembe véve, egy órát geostacionárius helyzetbe állítottak volna körülbelül 9000 méter tengerszint feletti magasságban, például a Mount Everest tetején ( kiemelkedés 8848 m), akkor körülbelül 39 órával megelőzné a tengerszintre beállított órát.^[4]^[5] A gravitációs idődilatáció ugyanis gyorsuló vonatkoztatási rendszerben vagy az ekvivalencia elv alapján masszív tárgyak gravitációs mezőjében nyilvánul meg.^[6]

Az általános relativitáselmélet szerint a tehetetlenségi tömeg és a gravitációs tömeg megegyezik, és az összes gyorsuló vonatkoztatási rendszer (mint például egy egyenletesen forgó vonatkoztatási rendszer a megfelelő sajátidő-dilatációval) fizikailag egyenértékű az azonos erősségű gravitációs mezővel.^[7]

Vegyünk egy megfigyelő csoportot egy egyenes "függőleges" vonal mentén, akik mindegyike különálló állandó g-erőt tapasztal a vonal irányába (pl. Hosszú gyorsuló űrhajó,^[8]^[9] felhőkarcoló, tengely a bolygón). Legyen $g(h)$ a g-erő, ami függ a "magasságtól", egy koordinátától a fent említett vonal mentén. Az egyenlet egy bázis megfigyelőhöz viszonyítva a $h=0$ van

T_{d}(h)=\exp \left[{\frac {1}{c^{2}}}\int _{0}^{h}g(h')dh'\right]

ahol $T_{d}(h)$ a teljes dilatáció egy távoli $h$ helyzetben mérve , $g(h)$ a g-erő függése a $h$ "magasságtól" , $c$ a fény sebessége, és $\exp$ hatványozást jelöl e-vel .

Az egyszerűség kedvéért egy Rindler-féle megfigyelők családjában egy sík tér-időben a függőség a következő lenne

g(h)=c^{2}/(H+h)

$H$ állandóval, amely ezt eredményezi

T_{d}(h)=e^{\ln(H+h)-\ln H}={\tfrac {H+h}{H}}

.

Másrészt, mikor $g$ majdnem állandó és $gh$ sokkal kisebb, mint $c^{2}$ , a lineáris "gyenge mező" közelítés is használható. $T_{d}=1+gh/c^{2}$

Lásd még az Ehrenfest-paradoxont, amikor ugyanezt a képletet alkalmazzuk egy forgó vonatkoztatási rendszerre sík tér-időben.

Forgást nem végző gömbszimmetrikus testen kívül

A gravitációs idődilatáció meghatározására használt közönséges egyenlet a Schwarzschild metrikából származik, amely a téridőt egy nem forgó, masszív, gömbszimmetrikus objektum közelében írja le. Az egyenlet az

t_{0}=t_{f}{\sqrt {1-{\frac {2GM}{rc^{2}}}}}=t_{f}{\sqrt {1-{\frac {r_{s}}{r}}}}=t_{f}{\sqrt {1-{\frac {v_{e}^{2}}{c^{2}}}}}=t_{f}{\sqrt {1-\beta _{e}^{2}}}

ahol

$t_{0}$ a két esemény közötti sajátidő egy megfigyelő számára, amely közel van a masszív szférához, vagyis a gravitációs mező mélyén
$t_{f}$ az események közötti koordinátaidő egy olyan megfigyelő számára, amely önkényesen nagy távolságra van a masszív objektumtól (ez azt feltételezi, hogy a távoli megfigyelő Schwarzschild-koordinátákat használ, egy olyan koordináta-rendszert, ahol a hatalmas tömegű gömbtől végtelen távolságban lévő órán egy másodperc telik el a koordinátaidő egy másodpercében, míg a közelebbi órák ennél kevesebbet ketyegnek),
$G$ a gravitációs állandó,
$M$ a gravitációs mezőt létrehozó objektum tömege,
$r$ a megfigyelő sugárirányú koordinátája a gravitációs mezőn belül (ez a koordináta analóg az objektum középpontjától való klasszikus értelemben vett távolsággal, de valójában ez egy Schwarzschild-koordináta; ebben a formában az egyenletnek valós megoldásai $r>r_{s}$ esetben vannak),
$c$ a fény sebessége,
$r_{s}=2GM/c^{2}$ a Schwarzschild-sugár az $M$ tömegű test esetében,
$v_{e}={\sqrt {\frac {2GM}{r}}}$ a szökési sebesség, és
$\beta _{e}=v_{e}/c$ a szökési sebesség, és a c fénysebesség hányadosa.

Ennek szemléltetésére, a forgás hatásainak figyelembevétele nélkül, a Föld gravitációs potenciáljának közelsége miatt a bolygó felszínén egy órán 0,0219 másodperccel kevesebb idő telik el egy év alatt, mint egy nagyon távoli megfigyelő óráján. Ehhez képest a nap felszínén 66,4 másodperccel kevesebb idő telik el ugyanezen egy év alatt.

Körpályák

A Schwarzschild metrikában a szabadon eső tárgyak kör alakú pályát is bejárhatnak, ha a pálya sugara nagyobb, mint ${\tfrac {3}{2}}r_{s}$ (a foton gömb sugara). A nyugalomban lévő óra képlete fentebb lett megadva; az alábbi képlet egy körpályán lévő óra általános relativisztikus idődilatációját adja meg:^[10]^[11]

t_{0}=t_{f}{\sqrt {1-{\frac {3}{2}}\!\cdot \!{\frac {r_{s}}{r}}}}\,.

Mindkét dilatációt az lentebbi ábra mutatja.

A gravitációs idődilatáció fontos jellemzői

Az általános relativitáselmélet szerint a gravitációs idődilatáció jelensége együtt jár a gyorsuló vonatkoztatási rendszer létezésével. Emellett hasonló körülmények között minden fizikai jelenség egyformán idődilatációt szenved, az általános relativitáselméletben alkalmazott ekvivalencia-elvnek megfelelően.
A területi fénysebesség mindig megegyezik c-vel az ott tartózkodó megfigyelő szerint. Vagyis a téridő minden infinitezimálisan kis régiójához hozzá lehet rendelni a saját sajátidejét, és a fény sebessége a sajátidő szerint ebben a régióban mindig c. Ez független attól, hogy egy adott régiót megfigyelő foglal-e el vagy sem. Időkésleltetést lehet mérni azon fotonok esetében, amelyek a Földből kibocsátódnak, a Nap közelében meghajlanak, a Vénuszra utaznak, majd hasonló úton haladnak vissza a Földre. Itt nem sérül a fénysebesség állandósága, mivel bármely megfigyelő, aki megfigyeli a fotonok sebességét a régiójukban, megállapítja, hogy ezeknek a fotonoknak sebessége c, miközben az a sebesség, amellyel a fényt megfigyeljük, véges távolságokat tesz meg a Nap közelében, különbözni fog c-től.
Ha egy megfigyelő képes távolról messzi területre követni a fényt, amelyet egy távoli, idődilatált megfigyelő elfog, aki közelebb van egy nagy tömegű testhez, akkor az első megfigyelő nyomon követi, hogy mind a távoli fénynek, mind annak a távoli dilatált megfigyelőnek lassabb az órája mint más fénynek, amely az első megfigyelőhöz érkezik c-vel, mint minden más fény, amelyet az első megfigyelő valóban megfigyelhet (a saját helyén). Ha a másik, távoli fényt végül elfogja az első megfigyelő, azt az első megfigyelő ugyancsak c-nek fogja mérni.
A gravitációs idődilatáció $T$ egy gravitációs potenciálban megegyezik a sebesség idődilatációjával egy olyan sebességnél, amely szükséges a gravitációs potenciál elhagyásához (tekintettel arra, hogy a metrika a következőképp alakul $g=(dt/T(x))^{2}-g_{space}$ , azaz időben változatlan, és nincsenek "mozgás" kifejezéső részek $dxdt$ ). Ennek bizonyítására Noether tételét alkalmazni lehet egy testre, amely a végtelenségtől kezdve szabadon esik a centrumba. Ekkor a metrika időbeli változatlansága a mennyiség megőrzését jelenti $g(v,dt)=v^{0}/T^{2}$ , hol $v^{0}$ a 4-es sebesség időösszetevője, $v$ a test sebességének 4-es vektora. A végtelenben $g(v,dt)=1$ , így $v^{0}=T^{2}$ , vagy a helyi idődilatációhoz igazított koordinátákban, $v_{loc}^{0}=T$ ; vagyis a megszerzett sebesség miatti dilatáció (a leeső test helyzetében mérve) megegyezik a gravitációs idődilatációval abban a potenciálban, ahová a test beesett. Ezt a bizonyítást általánosabban alkalmazva azt kapjuk, hogy (a metrikán ugyanazon feltételezések mellett) a két pont közötti relatív gravitációs idődilatáció megegyezik az alacsonyabb ponttól a magasabbig való felmászáshoz szükséges sebesség miatti idődilatációval.

Kísérleti megerősítés

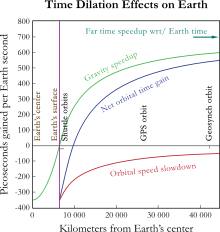
A gravitációs idődilatációt kísérleti úton megmérték repülőgépeken lévő atomórákkal. A repülőgépek fedélzetén lévő órák valamivel gyorsabbak voltak, mint a földön. A hatás elég jelentős már ahhoz, hogy a globális helymeghatározó rendszer mesterséges műholdjainak korrigálni kelljen az óráikat.^[12]

Mindemellett a laboratóriumban kísérletileg igazolták az egy méternél kisebb magasságkülönbségek miatti dilatációkat.^[13]

A gravitációs idődilatációt megerősítette a Pound – Rebka kísérlet, a Sirius B fehér törpe spektrumának megfigyelése és a Viking 1 Mars leszállóra küldött és onnan érkező időjelekkel végzett kísérletek is.

Lásd még

Fordítás

Ez a szócikk részben vagy egészben a Gravitational time dilation című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Hivatkozások

↑ Einstein, A.. Relativity : the Special and General Theory by Albert Einstein. Project Gutenberg (2004. február 1.)
↑ Uggerhøj (2016. december 21.). „The young centre of the Earth”. European Journal of Physics 37 (3), 035602. o. DOI:10.1088/0143-0807/37/3/035602.
↑ A. Einstein, "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen", Jahrbuch der Radioaktivität und Elektronik 4, 411–462 (1907); English translation, in "On the relativity principle and the conclusions drawn from it", in "The Collected Papers", v.2, 433–484 (1989); also in H M Schwartz, "Einstein's comprehensive 1907 essay on relativity, part I", American Journal of Physics vol.45,no.6 (1977) pp.512–517; Part II in American Journal of Physics vol.45 no.9 (1977), pp.811–817; Part III in American Journal of Physics vol.45 no.10 (1977), pp.899–902, see parts I, II and III.
↑ Hassani, Sadri. From Atoms to Galaxies: A Conceptual Physics Approach to Scientific Awareness. CRC Press, 433. o. (2011). ISBN 978-1-4398-0850-4 Extract of page 433
↑ Topper, David. How Einstein Created Relativity out of Physics and Astronomy, illustrated, Springer Science & Business Media, 118. o. (2012). ISBN 978-1-4614-4781-8 Extract of page 118
↑ John A. Auping, Proceedings of the International Conference on Two Cosmological Models, Plaza y Valdes, ISBN 9786074025309
↑ Johan F Prins, On Einstein's Non-Simultaneity, Length-Contraction and Time-Dilation
↑ Kogut, John B.. Introduction to Relativity: For Physicists and Astronomers, illustrated, Academic Press, 112. o. (2012). ISBN 978-0-08-092408-3
↑ Bennett, Jeffrey. What Is Relativity?: An Intuitive Introduction to Einstein's Ideas, and Why They Matter, illustrated, Columbia University Press, 120. o. (2014). ISBN 978-0-231-53703-2 Extract of page 120
↑ Keeton, Keeton. Principles of Astrophysics: Using Gravity and Stellar Physics to Explore the Cosmos, illustrated, Springer, 208. o. (2014). ISBN 978-1-4614-9236-8 Extract of page 208
↑ Taylor, Edwin F.. Exploring Black Holes. Addison Wesley Longman, 8-22. o. (2000. december 21.). ISBN 978-0-201-38423-9
↑ Richard Wolfson. Simply Einstein. W W Norton & Co., 216. o. (2003). ISBN 978-0-393-05154-4
↑ C. W. Chou, D. B. Hume, T. Rosenband, D. J. Wineland (24 September 2010), "Optical clocks and relativity", Science, 329(5999): 1630–1633;

További irodalom

Grøn, Øyvind. Einstein's Theory: A Rigorous Introduction for the Mathematically Untrained. Springer (2011. december 21.). ISBN 9781461407058

[1] Einstein, A.. Relativity : the Special and General Theory by Albert Einstein. Project Gutenberg (2004. február 1.)

[2] Uggerhøj (2016. december 21.). „The young centre of the Earth”. European Journal of Physics 37 (3), 035602. o. DOI:10.1088/0143-0807/37/3/035602.

[3] A. Einstein, "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen", Jahrbuch der Radioaktivität und Elektronik 4, 411–462 (1907); English translation, in "On the relativity principle and the conclusions drawn from it", in "The Collected Papers", v.2, 433–484 (1989); also in H M Schwartz, "Einstein's comprehensive 1907 essay on relativity, part I", American Journal of Physics vol.45,no.6 (1977) pp.512–517; Part II in American Journal of Physics vol.45 no.9 (1977), pp.811–817; Part III in American Journal of Physics vol.45 no.10 (1977), pp.899–902, see parts I, II and III.

[4] Hassani, Sadri. From Atoms to Galaxies: A Conceptual Physics Approach to Scientific Awareness. CRC Press, 433. o. (2011). ISBN 978-1-4398-0850-4 Extract of page 433

[5] Topper, David. How Einstein Created Relativity out of Physics and Astronomy, illustrated, Springer Science & Business Media, 118. o. (2012). ISBN 978-1-4614-4781-8 Extract of page 118

[6] John A. Auping, Proceedings of the International Conference on Two Cosmological Models, Plaza y Valdes, ISBN 9786074025309

[7] Johan F Prins, On Einstein's Non-Simultaneity, Length-Contraction and Time-Dilation

[8] Kogut, John B.. Introduction to Relativity: For Physicists and Astronomers, illustrated, Academic Press, 112. o. (2012). ISBN 978-0-08-092408-3

[9] Bennett, Jeffrey. What Is Relativity?: An Intuitive Introduction to Einstein's Ideas, and Why They Matter, illustrated, Columbia University Press, 120. o. (2014). ISBN 978-0-231-53703-2 Extract of page 120

[10] Keeton, Keeton. Principles of Astrophysics: Using Gravity and Stellar Physics to Explore the Cosmos, illustrated, Springer, 208. o. (2014). ISBN 978-1-4614-9236-8 Extract of page 208

[11] Taylor, Edwin F.. Exploring Black Holes. Addison Wesley Longman, 8-22. o. (2000. december 21.). ISBN 978-0-201-38423-9

[Wolfson-12] Richard Wolfson. Simply Einstein. W W Norton & Co., 216. o. (2003). ISBN 978-0-393-05154-4

[13] C. W. Chou, D. B. Hume, T. Rosenband, D. J. Wineland (24 September 2010), "Optical clocks and relativity", Science, 329(5999): 1630–1633;

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]