Gravitáció

Fekete lyuk gravitációs lencsehatása szimulált animáción

A gravitáció, más néven tömegvonzás egy kölcsönhatás, amely bármilyen két, tömeggel bíró test között fennáll, és a testek tömegközéppontjainak egymás felé ható gyorsulását okozza. A gravitációs erő a klasszikus fizikában az az erő, amelyet az egyik test a másikra a gravitáció jelenségének megfelelően kifejt.

Egy testre ható gravitációs erő az egyik – a Föld felszínén álló megfigyelő számára a legnagyobb – összetevője a test súlyának, a testre ható nehézségi erőnek. A Földhöz rögzített koordináta-rendszerben – amely nem inerciarendszer, hanem gyorsuló koordináta-rendszer – szemlélve a gravitációs erő mellett kisebb mértékben tehetetlenségi erők, a centrifugális erő, a Coriolis-erő és Föld nagyon kis mértékben változó szögsebességű forgása – szöggyorsulása – miatti Euler-erő is hozzájárul a nehézségi erőhöz.

Az általános relativitáselmélet ekvivalenciaelve szerint lokálisan megkülönböztethetetlen egymástól, hogy egy testre ható erő gravitáció vagy a koordináta-rendszer gyorsulása miatt lép-e fel.

Elméletek

Newton

A leeső test mozgásának okát elsőként Sir Isaac Newton azonosította egy erővel, amely a testre hat, és amelyet „univerzális gravitációs kölcsönhatás”-ként írt le Philosophiae Naturalis Principia Mathematica című könyvében. A később többek által kiegészített elmélet szerint két, tömeggel rendelkező test egymásra vonzerőt fejt ki, ez az erő a két test tömegközéppontját összekötő egyenesen helyezkedik el, és mindkét test tömegével arányos, ugyanakkor a testeket egymástól távolítva csökken. A gravitációs erő egyetlen feltétele és oka a testek tömege. Minden test, anyagi összetételétől, halmazállapotától, hőmérsékletétől függetlenül folyamatosan kifejti a tömegéből eredő vonzerőt. Az erő bármilyen távolságból hat, bár a távolsággal gyengül, és a gravitációs erő el nem téríthető és nem árnyékolható.

A gravitációs vonzerő nagysága a következő összefüggés szerint számítható ki:

$F_{\mathrm {grav} }=G{\frac {m_{1}m_{2}}{d^{2}}}$

ahol m₁ és m₂ a két test tömege, d a két test tömegközéppontja közti távolság, továbbá G a gravitációs állandó, amelynek ma elfogadott értéke (2018 CODATA):

$G=\left(6{,}67430\pm 0{,}00015\right)\cdot 10^{-11}\ {\mbox{m}}^{3}\ {\mbox{kg}}^{-1}\ {\mbox{s}}^{-2}\,$

Az összefüggés vektori alakban, azaz az (1)-es test az alábbi erővel vonzza a (2)-es testet, ha $\mathbf {d} _{1;2}$ az (1)-ből a (2)-be mutató vektor:

$\mathbf {F} _{1;2}=-G{\frac {m_{1}m_{2}}{|\mathbf {d} _{1;2}|^{2}}}{\frac {\mathbf {d} _{1;2}}{|\mathbf {d} _{1;2}|}}$

Szigorúan véve ez a törvény csak pontszerű objektumokra vonatkozik. Ha a tárgynak térbeli kiterjedése van, az erőt integrálszámítással kell megadni. Kimutatható, hogy ha a tárgy gömbszimmetrikus tömegeloszlású, akkor az integrálszámítás ugyanazt az eredményt adja, mintha a test pontszerű lenne. A tárgytól távolodva a kiterjedt valódi és a pontszerű elméleti tömeg közötti elvi különbség egyébként is egyre kisebb jelentőségűvé válik.

A gravitációs erő két tömeggel rendelkező test között sosem nulla, és értéke nullánál kisebb sem lehet. Negatív gravitáció, vagyis két test közötti gravitációs taszítóerő, ún. antigravitáció a jelen ismereteink szerint nem létezik.

Megjegyzendő, hogy noha később más elvekre épülő, finomított pontosságú elméletek is születtek a gravitáció jelenségére, a newtoni törvények hétköznapi körülmények között ma is teljesen pontosan leírják a jelenség működését, vagyis jól használhatóak.

Hasonló tömegű testeknél az egymás felé való elmozdulás már látható mértéket is öltene. A két test itt kezdetben egymáshoz képest áll, és a tömegvonzási erőn kívül más erő nem hat rájuk. Kattintson a képre.

Nem szabad megfeledkezni arról, hogy ha két testet megfigyelünk, akkor nem csak az egyik vonzza a másikat, hanem ugyanakkora, de ellentétes irányú erővel a másik is az egyiket, ez Newton harmadik törvényéből, a kölcsönhatás törvényéből következik. Tehát ha a két test szabadon mozoghat, akkor nem csak az egyik test kezd gyorsulni a másik irányába, hanem mindkét test elindul egymás irányába, egymás felé gravitálnak. Newton második törvénye szerint ez a gyorsulás az adott test tömegével fordítottan arányos, de sosem nulla. Azaz ha elejtünk egy téglát, akkor a tégla a földi nehézségi gyorsulással megindul a Föld tömegközéppontja felé, de valójában a Föld is elindul a tégla felé, csak a tömegük különbözősége miatt megmérhetetlenül kis mértékben.

A gravitáció newtoni elméletének megoldatlan hiányosságai vannak. Elsősorban kérdés maradt, hogy a tömegvonzást miféle közeg közvetíti. Tehát ahogy az elektromos és mágneses vonzást részletesen leírt tulajdonságú erőterek továbbítják, nem tudjuk, milyen erőtér, milyen részecskék adják át a tömegvonzást a másik testnek. Az ehhez feltételezett elemi részecskét, a gravitont máig nem sikerült kísérletileg kimutatni, noha folynak ez irányban kutatások. A kísérleteket külön nehezíti, hogy mivel a gravitáció leárnyékolhatatlan, a Földön és egyáltalán égitestek közelében nagyon nehéz ezek zavaró hatásától független méréseket végezni.

Einstein

Albert Einstein az 1916-ban megjelentetett második, általános relativitáselméletében a tömegvonzás jelenségére más elméleti leírást adott. Az elmélet szerint tömegvonzási erő nem létezik, így az azt közvetítő részecskét sem kell keresnünk. Ehelyett azt kell elképzelnünk, hogy egy test a tömegétől függő mértékben meghajlítja, elgörbíti maga körül a téridőt. A tér eme torzulása rajzon, maketten két dimenzióban úgy ábrázolható, hogy egy feszes gumilepedőre vagy gumihálóra rátesznek egy súlyos golyót. A golyó felé haladva az egyre meredekebbé váló felület érzékelteti a tér görbületének, és az ezzel ábrázolt gravitációnak az erősödését. Ha erre a felületre egy másik, kisebb golyót helyezünk, az a lejtős felület miatt a nagy golyó felé indul el, mintha az vonzaná magához.

Egy test (a fekete gömb) körül a tér úgy görbül, hogy a test felé lejt (szemléltető ábrázolás)

A modell matematikai eszközökkel is vizsgálható. Így kiderül, hogy a modell nincs ellentmondásban a newtoni elmélettel, hanem csak egy másik magyarázatot kínál a megfigyelt tömegvonzási jelenségekre. A testtől távolodva gyengülő gravitációs erőnek megfelel a torzult tér egyre kisebb „lejtése”. A hatalmas tömegű Nap körül a Föld pedig nem azért kering, mert a Nap egy erőt fejt ki rá valami nem tisztázott módon, hanem mert a Föld a Nap körül létrejött térbeli „gödör” lejtős oldalán szalad körbe, a sebességének köszönhetően mindig azonos magasságban maradva. A gödörmodell igazodik a Kepler-törvényekhez is, vagyis ha egy kisebb sebességű bolygót is elindítunk ebben a gödörben kisebb sugarú körpályán, akkor ez a bolygó gyorsabban fog keringeni, ahogy az a Naprendszer esetében is ismert.

Ne feledjük, hogy ez az előbb használt, gödörről és lejtőkről szóló modell csak egy kényszerűségből alkalmazott hasonlat, amely két dimenzióra egyszerűsítve mutat be a háromdimenziós tér torzulásai által okozott jelenségeket.

A modell értelmez egy másik, azóta megfigyelt, sőt ma már a csillagászok által a távoli világegyetem vizsgálatára gravitációs lencse formájában ki is használt jelenséget is. Tudjuk, hogy a fény mindig egyenes vonalban halad, a lehetséges legnagyobb sebességgel. Newton első törvénye szerint egy magára hagyott test egyenes vonalban, egyenletes sebességgel halad. Einstein az elméletéből azt a jóslatot vezette le, hogy nagy tömegű csillagok, galaxisok mellett elhaladva a fény az egyenes útvonalról letér, a pályája a nagy tömeg közelében valamennyire elhajlik. Annak ellenére hatni látszik rá a gravitációs erő, hogy a fénynek tulajdonképpen nincs is tömege. Newton elméletével ez így nem is lenne megmagyarázható, Einstein viszont ezt mondja: a fény részecskéi (a fotonok) nem egy erő hatására térülnek el egy nagy tömegű test gravitációjának hatására, hanem maga az egyenes vonal hajlik el a térrel együtt. Azaz a fény továbbra is egyenes vonalban mozog, csak ez az egyenes hajlik meg egy független külső megfigyelő számára. A test gravitációjának hatása alatt álló megfigyelő a fény útját továbbra is egyenesnek látja, mert az ő által érzékelt térben az a pálya valóban egybeesik az ő terének egy egyenes vonalával. A hipotetikusan előrejelzett jelenséget 1919-ben egy napfogyatkozás során angol csillagászok valóban megfigyelték, az előrejelzettel azonos mértékben, és így az elméletnek ezt a szakaszát kísérletileg igazolták is. Ez is mutatja, hogy Newton és Einstein modelljei között ha normál körülmények között nem is, kozmikus, extrém méretű jelenségekben már kimutatható eltérés. A nagy pontosságú megfigyelések Einstein elméletét igazolják.

A relativitáselméletben bemutatott gravitációmodell alapján gondolkodva tehát kijelenthetjük, hogy gravitációs erő valójában nincs is, csak a gravitáció jelensége létezik, „gravitációs hatásról” beszélhetünk, amelyet nem erőkkel, hanem a tér torzulásaival indokolhatunk.

A gravitációs hatás terjedési sebessége ebben a modellben is feltehető kérdés. Ha egy gondolatkísérletben egy tömeg hirtelen felbukkan a térben és azt meghajlítja maga körül, akkor ez a tértorzulás azonnal vagy valamilyen késéssel éri-e el a távol levő másik testet? Az azonnali terjedés végtelen sebességet feltételez, akkor pedig létezne a fénynél nagyobb sebességgel terjedő fizikai hatás, amit viszont a relativitáselmélet kizár. A véges terjedési sebesség következtében pedig egy, a térben haladó tömeg által okozott térgörbület hasonló módon terjed a test körül, mint ahogy egy előre haladó csónak kelti ék alakú orrhullámát a víz felszínén. Ezt az elvi megfontolást kiteljesítve előrejelezhető, hogy az aszimmetrikus gyorsuló (változó sebességű vagy irányú) mozgást végző testek hullámszerű zavart keltenek a térben. Ezek a hatások csak igazán nagy tömegek hatókörében lehetnek megfigyelhetőek, például összeomló vagy egymásba rohanó csillagok által létrehozva. Az így leírt, már Einstein által is tárgyalt gravitációs hullámokat kísérletileg először a LIGO Tudományos Együttműködésnek sikerült igazolnia, melyet 2016. február 11-én jelentettek be, igazolva ezzel Einstein legutolsó jóslatát. (A megfigyelés 2015. szeptember 14-én történt.) Más, közvetett módszerrel már 2003-ban sikerült bizonyítani, hogy a gravitációs hatás fénysebességgel terjed.

Mások

Nikola Tesla kétségbe vonta Albert Einstein relativitáselméletét, bejelentve, hogy ő a gravitáció dinamikus elméletén dolgozik (amelyet még 1892 és 1894 között kezdett el). Úgy érvelt, hogy egy „erőtér” feltételezése sokkal jobb koncepció lenne és az elektromágneses energia közegére fókuszált, amely kitölti a matematikailag definiált teret és ezáltal az egész általunk belátható világűrt.

A Világegyetemet kitöltő sötét anyag és az Univerzumot mozgató sötét energia kutatásakor fölmerült, hogy gravitációs centrum nem csak tömeggel bíró test lehet, azaz "minden tömeggel bíró test gravitációs erőt fejt ki, de nem minden gravitáció származik tömeggel bíró testtől". A sötét anyag és energia korunk természettudományának egyik legnagyobb rejtélye, a kérdés eldöntése még évtizedeket vehet igénybe.

A sötét energia jellegének egyik lehetséges leírási módja szorosan összefügg a Newton-féle gravitációs állandó univerzalitásának a hangsúlyozásával, amennyiben értéke megadható a $c^{5}\cdot {\frac {t_{U}}{G}}$ összefüggéssel. Ebben c a vákuumbeli fénysebesség, $t_{U}$ pedig a Metagalaxis "életkora", ami jelenlegi ismereteink szerint 13,72·10⁹ év. Az így definiált energiaérték 1,571·10⁷⁰ joule, s ez valóban megfelel a csillagászati kutatások eredményeként posztulált energiaértéknek.

Kísérletek

Cavendish torziós mérlege

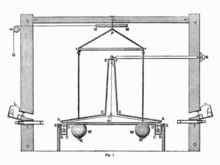
A gravitáció jelenségeinek szabályai szerint minden tömegnek van gravitációs hatása. Nagy tömegek, égitestek tömegvonzásának következményei az égbolton jól láthatóak, de sokkal kisebb tömegek vonzereje is megmérhető, különlegesen érzékeny eszközökkel. Ilyen eszköz a torziós mérleg, amelyet Henry Cavendish használt először a fentebb említett gravitációs állandó pontos megmérésére.

Ezt az ingát Eötvös Loránd többféle módon is továbbfejlesztette. Ezekkel a műszerekkel nagy pontosságig sikerült igazolni a tehetetlen és gravitációs tömeg egyenértékűségét, amely az egyik alapaxiómája az általános relativitáselméletnek is. Az Eötvös-inga egy másik változata pedig alkalmas arra, hogy a földfelszín alatti kőzet összetételéről, az ott rejlő, bányászati szempontból értékes anyagtömegek elhelyezkedéséről tehessenek már kielégítő pontosságú becsléseket, kihasználva, hogy a különböző sűrűségű, egyenetlenül elhelyezkedő ásványrétegek, olajlelőhelyek eltérő tömegvonzása kis mértékű aszimmetriát okoz a felszínen az ingára ható gravitációs erőkben.

Következmények

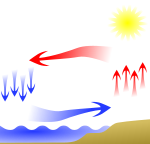
Nyilvánvaló, hogy többnyire a gravitáció az oka a nehézkedés és a súly jelenségeinek, bár ezek más hatás nyomán is létrejöhetnek. De a nehézkedés megteremtésével a Föld gravitációja számos alapvető és fontos jelenség előidézője.

A nehézkedés eredménye a súly, és így a fajsúly is, amely viszont a fajsúly (sűrűség) szerinti függőleges elrendeződést eredményezi. Ennek következménye az is, hogy a meleg levegő a hideg levegő fölé emelkedik, ami az alapja bolygónk teljes időjárásának, a szélnek, az égövi hőmérsékletek alakulásának, a felhőket létrehozó feláramlásoknak és a csapadékzónák mozgásának.

A meleg levegő felfelé áramlásának az eredménye a tűzgyújtás is. A tűzben a felhevült levegő, magával sodorva a parázsló koromszemcséket, felfelé törekszik – ez a láng –, megnyitja az utat az alul a tüzelőanyaghoz áramló friss levegőnek, ami az égést táplálja. Súlytalanságban a láng gömb alakúvá zárul az égő anyag körül, ami a kísérletek szerint ha már stabilizálódott, nem alszik el, viszont csak jól éghető anyag gyújtható meg.

A nehézkedésnek köszönhető az, hogy járni tudunk a talajon, mivel ehhez egyrészt a súlypontunk áthelyezését alkalmazzuk, másrészt a talpunk és a talaj közötti súrlódásra is szükség van, amely csak akkor lép fel, ha a két felületet egy erő, esetünkben a súlyerő összenyomja. Hasonlóképp lehetetlen lenne az autók, kerékpárok, mozdonyok közlekedése a súrlódás hiányában.

Végül a nehézkedésnek köszönhető a hidrosztatikai felhajtóerő jelensége, és az ennek eredményeként létrejövő úszás. Ami mindenfajta vízfelszíni közlekedés és vízi szállítás alapja.

Ám ezeken a nehézkedési jelenségeken kívül közvetlenül a gravitációnak más következményei is ismertek, ezekből következik néhány.

Égitestek

Az Univerzum anyaga a jelenleg leggyakrabban hallott elmélet szerint az Ősrobbanás során keletkezett, és annak energiájával szóródott szét a térben. Ahhoz, hogy a térben egyenlőtlenül szétterjedt gáz atomjai, egyszerű molekulái porszemcsékké álljanak össze, a saját tömegvonzásuk parányi erejére volt szükség. És ezek a porszemcsék ugyancsak a gravitációjuk hatására álltak össze, nagyon lassan, kisebb rögökké, végül egész égitestekké, az óriáscsillagoktól a kavicsnyi meteorokig. Ha az összetapadt anyagnak a tömege már elég nagy lett, akkor a saját gravitációjának hatására gömbszerű alakzatba tömörült, épp ez a lényeges megkülönböztető jegy választja el a gömbszerű törpebolygók és a szabálytalan formájú kisbolygók csoportját az IAU 2006-os kongresszusán hozott döntés szerint. Ugyanezt a gömbszerű alakot vették fel a nagyobb tömegű égitestek is, a holdak, a bolygók és a csillagok.

Az Orion-köd. A mérhetetlenül nagy gázködből még mindig születnek új csillagok

A legújabb megfigyelések szerint viszont az üstökösmagoknak és kisbolygóknak legalább egy része nem a korábban feltételezett, tömör, sziklaszerű tömbbé állt össze, hanem a világűr hidegében megfagyott gáz által összekötött porszemcsék szerkezete inkább a megszilárdult cukorhab törékenységéhez lehet hasonló. Ennek az oka az, hogy ezeknek a kis égitesteknek a gravitációja ennél erősebb tömörödésre nem kényszeríti az anyagukat.

Ha viszont az anyagcsomó tömege nagyon nagy, akkor ennek a gravitációja annyira összepréselheti az anyagát, hogy a belsejében már egy fúziós reakció indul be, és az égitest csillaggá válik. Ez a fúzió lehet robbanásszerű is, mint ami a nóvák esetében történik, amikor egy csillag a társcsillagától ragad el nagy mennyiségű anyagot, ami végül burokszerűen robban le róla. Egyes típusú csillagoknál az elszívott anyag olyan nagy sűrűségűvé tömörödik, hogy a beinduló fúzió egy szupernóva elképzelhetetlenül hatalmas robbanásában szórja szét a csillag anyagát, aminek az elméletek szerint a Naprendszerünk kialakulásának felgyorsulását és a Földön található nehezebb elemek létezését köszönhetjük.

Naprendszer

Mára teljesen ismertté és elfogadottá vált a néhány száz évvel ezelőtt még hevesen támadott tény, hogy a Föld bolygótársaival együtt a Nap körül kering, a Naprendszerünket alkotva. A keringő mozgás a Naptól kifelé ható centrifugális erőt hoz létre, amelyet a Nap gravitációs ereje ellensúlyoz, megközelítőleg körpályán tartva a bolygókat. Ha a Nap tömege és tömegvonzási ereje a mainál kisebb vagy nagyobb lenne, akkor a Föld keringési pályája is más távolságban lenne, és a Földön valószínűleg nem is jött volna létre a szárazföldi élet. (Megjegyzendő, hogy ha a Napnak más lenne a tömege, akkor sugárzásának ereje és összetétele is más lenne, igazodva a csillagfejlődés törvényeihez.) Ha a Nap gravitációja megszűnne, a Föld a pillanatnyi pályáját egyenesen folytatva, megtartva mostani 30 km/s sebességét, elszáguldana a csillagközi térbe.

A gravitációs erő fentebb látható képletét felhasználva kiszámíthatjuk a Nap és Föld között fennálló erőt, amelynek értéke 3,54 × 10²² newton. Ez a borzalmas erő háromszor akkora, mint amennyit egy képzeletbeli mérleg mutatna itt a Földön, ha rátehetnénk az egész Plútót. Ekkora erő kell ahhoz, hogy a Föld a körpályán maradjon.

Az alábbi táblázat azt sorolja fel, hogy melyik égitest mekkora tömegvonzási erőt gyakorol egy 1 kg tömegű testre, amelyet a Föld felszínén elhelyezünk. A kétféle érték a keringő égitestek változó távolságai közül a lehetséges legnagyobb és legkisebb távolságot veszi alapul. Érdekességként megjegyezhető, hogy a hatás–ellenhatás törvénye szerint az 1 kg-os test ugyanekkora erőkkel vonzza az égitesteket.

1 kg-ra	leggyengébb (N)		legerősebb (N)
Föld	9,81
Nap	5,90 × 10−3	0,00590	6,14 × 10−3	0,00614
Hold	2,90 × 10−5	0,0000290	3,87 × 10−5	0,0000387
Merkúr	4,47 × 10−10	0,000000000447	3,71 × 10−9	0,00000000371
Vénusz	4,77 × 10−9	0,00000000477	2,25 × 10−7	0,000000225
Mars	2,66 × 10−10	0,000000000266	1,41 × 10−8	0,0000000141
Jupiter	1,35 × 10−7	0,000000135	3,66 × 10−7	0,000000366
Szaturnusz	1,38 × 10−8	0,0000000138	2,64 × 10−8	0,0000000264
Uránusz	5,81 × 10−10	0,000000000581	8,68 × 10−10	0,000000000868
Neptunusz	3,10 × 10−10	0,000000000310	3,67 × 10−10	0,000000000367

A fenti számok szerint a Nap, mellette talán még a Hold gravitációs ereje is számottevőnek nevezhető, a többi bolygóé viszont már lényegében elhanyagolható. Különösen azért, mert a Föld gravitációja, annak földrajzi helytől függő ingadozásai ezeket az erőket észlelhetetlenné teszik. Sőt nem is szükséges bolygónyi méretekre hagyatkoznunk. A gravitációs erő képletét és a felsorolt számokat felhasználva megállapíthatjuk, hogy ha egy hétköznapi V43-as villanymozdonyt 40 méterre megközelítünk, akkor a mozdony már akkora gravitációs erővel hat ránk, mint amekkorával a Merkúr bolygó, a hozzánk legközelebbi helyzetében. Ennek négyszerese, tehát például egy egész vonat, vagy nagy panelház tömegének vonzereje már a Mars legnagyobb ránk gyakorolt gravitációs erejével egyezik meg. De ha egy kis termetű (56 kg tömegű) embertől 1 méterre állunk, az ő vonzereje szintén megegyezik a Merkúr legnagyobb vonzásával.

Ezek fényében feltehető a kérdés, hogy az asztrológia, amely a horoszkópjaiban a bolygók életünkre gyakorolt hatásáról tesz megállapításokat, vajon milyen fizikai hatás következményének tekinti az égitestek általuk precízen leírt befolyásoló erejét, ha ekkora távolságokból a gravitációs erő és az elektromágneses hullámok (fény) jelentéktelenségéről a számok és a rengeteg mérés révén meggyőződhettünk.

Az erők jelentéktelensége ellenére azonban tény, hogy a kozmoszban a Nap körül súlytalanul keringő égitestekre, kisbolygókra, üstökösökre ható, több százezer év alatt összegződő gravitációs hatások már képesek a keringési pályákon módosítani, így a csillagászok kénytelenek az égitestek perturbációs erejével is számolni például ún. földsúroló kisbolygók, visszatérő üstökösök, de még űrszondák pályájának kiszámításakor is.

Árapály

a Hold által okozott árapály jelenségének erősen eltúlzott arányú, vázlatos ábrázolása

Az árapály jelensége a Földön elsősorban a Hold, másodsorban a Nap gravitációs erejének a következménye. Ahogy a nagyon vázlatos ábrán látható, a Hold a Föld hozzá közelebb eső részét jobban vonzza, mint a távolabbi részt, és a Föld felszíne ennek a vonzásnak engedelmeskedve a Hold felé púposodik. A víz jobban formálható, ezért ez a dagálykúp a nagy kiterjedésű tengereken figyelhető meg a leginkább, ahol a Hold felé eső részre áramlik át a vizek egy kis része, a tenger szintjének emelkedését, máshol pedig csökkenését eredményezve. Ez a szintemelkedés sok más tényezőtől is függ, összességében csak néhány méter mértékű. A Föld szilárd felszínének megemelkedését is megfigyelték már, pontos mérések révén, és az mindössze centiméternyinek bizonyult.

A tudósok az árapálynak a Föld történetében, az élővilág kialakulásában fontos szerepet tulajdonítanak. A dagálykúp a Föld gyorsabb forgása miatt "előresiet", és az, hogy az aszimmetrikus tömegeloszlást létrehozó dagálykúpot a Hold maga felé vonzza, a Föld forgásának mikromásodpercnyi, de folyamatos lassulását eredményezi.

A függőleges

A kéregben vetődések, geológiai átrendeződések miatt a kőzet egyenetlen sűrűségű

Az Eötvös-ingával végzett mérésekből, és persze számos más jellegű mérésből is tudjuk, hogy a Föld anyagösszetétele nem egyenletes, nem gömbszimmetrikus. A hozzánk legközelebb eső rétegben, a kéregben is változó összetételű, változó sűrűségű, kilométeres nagyságrendben kifejezhető anyagtömbök, átrendeződések vannak. Ha a felszín alatt tőlünk jobbra egy nagy vasércmező rejtőzik, balra pedig egy vízzel feltöltődött karsztbarlang-rendszer, akkor tőlünk jobbra van a nagyobb átlagsűrűségű kéregszelvény, amelynek ebből eredően nagyobb a gravitációja. Ha most például egy függőónt egy nagyon precíz módszerrel megnéznénk, akkor azt láthatnánk, hogy az egy kicsit jobbra, a vasércmező felé tér el az elméleti, geometriai, a Föld középpontjához húzott függőleges iránytól, hiszen tőlünk jobbra nagyobb gravitációjú anyag van, mint balra. (Az egyik Eötvös-inga pontosan ezt a rendellenességet méri meg nagy érzékenységgel.) Mivel a "függőleges" számunkra arra mutat, amerre a leejtett tárgy esik, ezért ez az irány a Föld felszínén ide-oda kitér az elméleti irányhoz képest. Az eltérés a gyakorlatban lényegtelen mértékű, de nagy precizitást igénylő helyzetekben már számításba kell venni. (A függőleges irányt befolyásoló egyéb egyéb tényezők mellett.)

A Föld középpontja

A Föld felszíni gravitációs erejének szabálytalanságát ábrázoló képsorozat, a GRACE műholdprogram eredményei alapján

A jobbra látható egyszerű illusztráció a NASA 2002-ben kezdődött GRACE műholdprogramjának mérései alapján készült, amely kifejezetten a Föld gravitációs terének igen pontos megmérésére indult. Az ábra, amely kinagyítható, kilenc lépésben körüljárja a Földet, és eltérő színekkel ábrázolja a földfelszínen, azonos földrajzi magasságon érvényes tömegvonzási értékeket. Az ábrán nem a Föld alakja látható, hanem a tömegvonzásának helytől függő nagysága, a láthatóság kedvéért nagyon eltúlzott léptékben mutatva.

Azt tudjuk, hogy ha a felszíntől távolodunk, magasabbra emelkedünk, akkor a ránk gyakorolt tömegvonzás – ennek folyományaként a súlyunk – folyamatosan, apró mértékben csökken. Feltételezhetnénk, hogy ha viszont nem változtatjuk a magasságunkat, és így körbeutazzuk a világot, akkor a Föld tömegvonzása mindvégig állandó lesz. Az ábra azt mutatja be, hogy ez nem így van. Ha ugyanis a vörös, sőt, bíbor színnel jelölt területekre utazunk, tehát például Izlandra vagy Új-Guineára, akkor ott egy kicsivel erősebbnek mérhetnénk a Föld vonzerejét, mint ha ugyanabban a magasságban egy pontos mérést végeznénk a sárga, zöld, leginkább a cián színű területeken, például Srí Lanka szigetén. Az eltérés oka tulajdonképpen ugyanaz, mint ami már az előző szakaszban, kis területekre vonatkozóan olvasható volt, vagyis a Föld anyagának nem teljesen egyenletes eloszlása, változó sűrűsége, ebből következően a tömegének aszimmetriája, ami a gravitációra is hatással van.

A két szélső helyzet, tehát a bíbor és a cián területek között a gravitációs erők különbsége 120-130 mGal, ami a szabványos felszíni gravitáció 0,012–0,013%-a, azaz 10⁻⁴ nagyságrendű.

Ha a rajzzal ábrázolt gravitációs potenciálfelület egy "lejtős" részén, például Szumátra szigetén egy Eötvös-ingával precíz mérést végeznénk, azt láthatnánk, hogy a fizikai függőleges iránya eldől az elméletihez képest, mert tőlünk keletre erősebb, nyugatra gyengébb a földfelszíni tömegvonzási erő.

A bemutatott szabálytalanságból az is megállapítható, hogy a forgó Föld geometriai középpontja és a Föld gravitációs középpontja (egyben tömegközéppontja) nem esik egybe. Geometriai szempontból az előbbit, fizikai szempontból az utóbbit nevezhetjük a Föld középpontjának.

Műholdak

Az erősen torzított arányú ábra mutatja, ahogy a műhold váltakozó tömegű felszíni rétegek fölött halad el

Egy műhold, egy leegyszerűsítő fizikai modellben, a Föld tömegközéppontja körül kering, mivel bolygónk tömegvonzását innen induló erőnek tekintjük. Ez a tömegközéppont, ahogy az előző fejezetben olvasható, nem a Föld mértani középpontjában van, és a Föld felszínközeli tömegeloszlásában jelentős globális egyenetlenségek vannak. Ugyan a műholdak nagy része és az űrhajók a Föld felszínétől számított 250-400 kilométer magasságban keringenek, amely roppant nagy távolságnak tűnik, de ez a távolság nem elég nagy ahhoz, hogy a keringés közben a bolygó sűrűbb vagy könnyebb részei fölött elhaladva az ingadozó gravitáció ne legyen a műholdra hatással. Hiszen a műholdak a világűrben súrlódástól és más visszatartó erőtől szabadon mozognak, és a sok-sok keringés közben apránként összegződő eltérítő hatást már nem lehet figyelmen kívül hagyni. Annál is inkább, mivel ha megnézünk egy méretarányos rajzot, ha a Föld sugarát 100%-nak vesszük, akkor látjuk, hogy a műholdak pályája ennél csak 4-6%-kal van távolabb a bolygó középpontjától, ami a zavaró hatások szempontjából igazán nem nagy távolság.

Az ingadozó helyi gravitáció miatt a műhold pályájának magassága is mutat kis ingadozást, alacsonyabban van az erősebb gravitációjú területek, például Izland fölött, magasabban az óceánok fölött. Kis ingadozást mutat, részben emiatt a műhold sebessége is, és oldalirányú pályaingadozás is jelentkezik. Hosszú távra előrejelezni kívánt műholdpályák tervezésekor ez a hatás éppúgy számításba veendő, mint a Naprendszer többi bolygóinak a gravitációs hatása, a Nap és a Hold erős hatásainak kiegészítéséül.

A Föld precessziója

A Föld precessziója

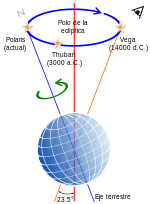
Ha egy forgó gömböt súlytalanságba és minden egyéb hatástól mentes környezetbe helyezünk, akkor a gömb a forgástengelye körül a végtelenségig foroghat. De ha a gömbre valamilyen kitérítő erőt gyakorolunk, akkor a gömb forgástengelye elbillenve forogni kezd egy láthatatlan kúpfelszínt követve. Pörgettyűvel, búgócsigával ez a jelenség nagyon egyszerűen megfigyelhető. Ezt a jelenséget precessziónak hívják, és a forgó Föld esetében is megfigyelhető. A precesszió kialakulásához viszont valamilyen zavaró hatás szükséges, és ilyen zavaró hatást a Nap és a Hold is bőségesen produkál. Ezekhez kis mértékig hozzájárul a Föld egyenetlen tömegeloszlása is, amely a tektonikai mozgások következtében lassan még változik is. Mivel a bolygó eltérő sűrűségű részeinek más a tömegvonzása, ez az aszimmetria a Hold és a Nap felé irányuló vonzóerőben is jelentkezik, amelynek eredményeként még maga a precesszió is szabálytalanná válik, a tengely ingadozása is ingadozik, és a csillagászok és ősgeológusok számára számításba veendő tényezőt képeznek.

Lásd még: Nutáció

GPS

A Globális Helymeghatározó Rendszer műholdjain igen nagy pontosságú órák működnek, mert az idő az egyik fontos alapja a rendszer működésének, a helymeghatározás pontossága az időmérés pontosságától függ. A műholdak kb. 26 600 km sugarú pályán (20 200 km-rel a föld felett) keringenek Ebből a tényből két érdekes hatás ered, amelyek a műholdak óráit befolyásolják, és mindkettőt az einsteini relativitáselméletek jósolták meg. Az első hatás az, hogy mivel a műholdak nagy sebességgel haladnak az űrben, az idődilatáció jelenségének megfelelően a fedélzetükön az idő egy egész kicsit lassabban telik. Tehát a műhold órája a Földi órákhoz képest naponta kb. 7 mikroszekundumot késik. Ám azt is tudjuk, hogy az idő az erősebb gravitáció által uralt térben is lassabban telik. Márpedig a műhold távolabb van a Földtől, mint mi a felszínen, kisebb gravitációs térben, emiatt a jelenség miatt a műhold órája naponta kb. 46 mikroszekundumot siet. A két számból következik, hogy a kilövés előtt a műholdak óráit úgy kellett beállítani, hogy a földi órákhoz képest azok naponta 39 mikroszekundumot késsenek, és ez a késés a pályára állítás után megszűnik.

Extrém gravitáció

“Cheshire Cat” galaxiscsoport a Nagy Medve csillagképben, a nevét Lewis Carroll Alice Csodaországban című művének folyton vigyorgó macska szereplőjéről kapta. Két fényes elliptikus galaxis körül található négy galaxisból jövő sugárzásra erős gravitációs tér hat

Einstein térgörbület-modelljében a gravitáció jelenségét olyan egyszerűsített módon magyaráztuk, hogy a tér a gravitáló test, például egy csillag felé "lejt". Vagyis ha egy űrhajóval a csillag irányába repülünk, a gravitáció még gyorsítja is a hajónkat, viszont ha sarkon fordulunk, és távolodni kezdünk a csillagtól, akkor mintegy "felfelé megyünk a lejtőn", és a hajót a csillag vonzása lassítani próbálja.

A kozmológusok, akik a csillagok fejlődésének szabályait és állomásait sok éve elemzik, azt állítják, hogy a csillagok egyik típusa az élete végén a saját rettenetes gravitációjának a hatására összeroppan, és egy elképzelhetetlenül sűrű anyagból álló, akár csak néhány kilométer sugarú gömbbé zsugorodik, neutroncsillag lesz belőle, amely mellesleg rendkívül gyorsan forog a tengelye körül. Mivel ebben egy egész csillag teljes anyaga, tömege van összezsúfolva, a kis méret ellenére igen nagy a tömegvonzása. Ha az előbbi űrhajóval közelítenénk hozzá, akkor a csillag alaposan hozzátenne a sebességünkhöz, ám ha távolodni próbálnánk tőle, akkor csak úgy tudnánk a vonzásából kimenekülni, ha a hajónk sebessége nagyon nagy lenne. Mondhatjuk, hogy a neutroncsillag felé közeledve a tér "lejtése" már nagyon meredekké válik, amelyen csak nagy erővel, nagy lendülettel lehet feljebb kapaszkodni. Ha valami elképzelhetetlenül teherbíró technikai megoldással leszállnánk egy neutroncsillag felszínére, akkor akár a fénysebesség felével is repülni képes űrhajóra lenne szükség, hogy fel tudjunk róla szállni és el tudjuk a csillag térségét hagyni.

A gravitációs kút valójában egy nagyon nagy tömegű csillag körül meggörbült térre alkotott hasonlat

Az ilyen szupersűrű csillagok körüli teret – érthető hasonlattal – gravitációs kútnak nevezik.

Nincs elméleti akadálya annak, hogy elképzeljünk egy olyan szupersűrű égitestet, amelynek a tömege egy óriáscsillagéval egyezik meg, és így a saját súlya alatt még a neutroncsillagnál is sűrűbb gömbbé zsugorodjon össze. Bizonyos tömeg felett arra lehet már számítani, hogy ha ennek a csillagnak a felszínére szállnánk le, akkor már a fénysebességnél is gyorsabb űrhajó kellene ahhoz, hogy onnan kiszabaduljunk, hogy a gravitációs kút nagyon-nagyon meredek képzeletbeli "falán" felmásszunk. Ám Einstein elméleteinek egyik ismert végkövetkeztetése, hogy a fénynél gyorsabban semmi sem haladhat. Vagyis ha egy ilyen csillaghoz egy határnál – a Schwarzschild-sugárnál – közelebb merészkedünk, akkor már fénysebességgel sem tudunk tőle elszakadni. Persze érvényes ez magára a fényre is, ezért az ilyen feneketlenné vált gravitációs kútból ő sem tud kijönni, aminek az a következménye, hogy erről az égitestről semmiféle sugárzás, semmilyen fény nem tud kilépni. Ez pedig azt jelenti, hogy ez a csillag, onnan induló fény híján, láthatatlan lesz számunkra. Olyan, mint egy nagyon apró fekete lyuk az égbolton.

Természetesen nincs ott semmiféle lyuk, ez csak egy tréfás hasonlat, az sem lehetséges, hogy ezen a lyukon átrepüljünk valahová, hiszen a hasonlat csak azt takarja, hogy ott egy mindent magához ragadni képes, szupersűrű, emiatt nem látható égitest van a világűrben. Amelynek a kozmológusok, asztrofizikusok számos érdekességét megjósolták elméleteikben, és ezeknek egy részét már sikerült megfigyelésekkel is valószínűsíteni, például a Hubble- és Spitzer-űrtávcsövek felvételeinek aprólékos elemzése révén. Azt a képzeletbeli gömbfelszínt a csillag körül, amelyen belülre kerülvén már fénysebességgel sem tudunk menekülni, hívják a fekete lyuk eseményhorizontjának.

Érdekességként elmondható, hogy ha valamiért űrhajóval egy fekete lyuk felé repülnénk, akkor nem úgy tűnnénk el a világ szeme elől, mint amikor a golflabda belepottyan a lyukba. Az óriási gyorsasággal forgó fekete lyuk gravitációja először arra kényszerítené az űrhajónkat, hogy keringeni kezdjen körülötte, egyre nagyobb sebességgel, éppúgy, mint ahogy az a fürdőkádból leengedett vízen úszó apró szivacsdarabbal is megfigyelhető a lefolyó körül. És amikor a csillagba zuhanó többi anyaggal való ütközések lelassítják az űrhajónkat, akkor kerülnénk csak egyre közelebb a csillaghoz, míg végül a hatalmas gravitációjú, nagyon közel került csillag ereje széttépne mindent.

Noha egy fekete lyuk megközelítésének veszélye még jó ideig nem fenyeget egyetlen embert sem, megnyugtató tudnunk, hogy a fekete lyuk gigantikus gravitációja és a körülötte keringésünk óriási sebessége a relativitáselmélet alapján annyira lelassítaná hajónkon az idő múlását, hogy mi a fedélzeten az egész jelenséget másodpercek alatt éreznénk megtörténni.

Források

• ↑ Science.nasa.gov: Not Just Another Old Flame Archiválva 2011. január 13-i dátummal a Wayback Machine-ben (NASA Science)
• ↑ Tuztorony.hu: Meggyullad-e a gyertya a súlytalanság állapotában? Archiválva 2011. január 4-i dátummal a Wayback Machine-ben (Tűztorony.hu)
• ↑ NASA Technical Reports: (NASA Technical Reports Server)
• ↑ Kereszturi Axioma: Dr. Kereszturi Endre: AXIOMA PHYSICA HUNGARICA - természeti állandók egységes elméletének axiomatikus megalapozása

További információk

• https://qubit.hu/2018/03/07/miert-gorbul-a-ter
• Richard Panek: Mi a baj a gravitációval? (Scolar, 2020)
• Emilio Segré: Die grossen Physiker und ihre Entdeckungen (Piper Sonderausgabe, 1997)
• http://physics.nist.gov/cuu/Constants/Table/allascii.txt (angol)
• J.D. Bernal: A fizika fejlődése Einsteinig (Gondolat/Kossuth, 1977)
• Hraskó Péter: Relativitáselmélet (Typotex, 2002)
• Albert Einstein: A speciális és általános relativitás elmélete (5. kiadás, Gondolat, Budapest, 1978)
• Albert Einstein: Grundzüge de Relativitaetstheorie (VIEWEG - 6. Auflage 1990.)
• Max Born: Die Relativitaetstheorie Einsteins (Springer, 1984)
• George Gamow - John M. Cleveland: Fizika (2. kiadás, Gondolat, Budapest, 1977)
• William J. Kaufmann, III – Relativitás és kozmológia (Gondolat, Budapest, 1985)
• szerk.: Dr. Szilágyi Miklós: Fizikai kislexikon. Műszaki Könyvkiadó, Budapest (1977). ISBN 963 10 1695 1 
• How Stuff Works: How does gravity work? (angol)
• Űrhajókkal, lézersugárral igazolják Einstein gravitációs hullám-elméletét (LISA-program) (Transindex, 2010. május 11.)
• Javítottak a gravitációs hullámok észlelésén (Index, 2010. december 9.)
• A Föld gravitációs térképe (Index - Tudomány)
• Bevezetés az űrgravimetriába (Magyar Űrkutatási Iroda)
• What the Global Positioning System Tells Us about Relativity (angol)