Szerkesztő:Szaszicska/Vegyérték-elektronpár taszítási elmélet
A vegyérték-elektronpár taszítási elmélet (angol rövidítéssel VSEPR-elmélet) a molekulák térszerkezetét írja le a központi atom körüli elektronok száma alapján.[1]
Az elmélet feltevése, hogy az atomok vegyérték-elektronpárjai taszítják egymást, így olyan elrendeződést vesznek fel, amelyben a taszítás a lehető legkisebb mértékű, meghatározva ezzel a molekula térszerkezetét..
Az elméletet régóta kritizálják amiatt, hogy nem kvantitatív, és emiatt a molekulageometriának csak "nyers" (bár szerkezetileg helyes) megadására képes.[2]
Description
[szerkesztés]VSEPR theory, occasionally pronounced "vesper" or "vuh-seh-per",[3] is used to predict the arrangement of electron pairs around non-hydrogen atoms in molecules, especially simple and symmetric molecules, where these key, central atoms participate in bonding to 2 or more other atoms; the geometry of these key atoms and their non-bonding electron pairs in turn determine the geometry of the larger whole.
The number of electron pairs in the valence shell of a central atom is determined after drawing the Lewis structure of the molecule, and expanding it to show all electron-pair bonds and lone pairs *of* electrons.[4] For the purposes of VSEPR theory, the multiple electron pairs in a double bond or triple bond are treated as though they were a bond with single pair of electrons.[4] In cases where a molecule can be depicted by two or more resonance structures, these structures generally differ only by the interchange of double and single bonds, so that they have the same steric number and therefore the same VSEPR model.
The electron pairs are assumed to lie on the surface of a sphere centered on the central atom and tend to occupy positions that minimizes their mutual repulsions by maximizing the distance between them.[4][5] Gillespie has emphasized that the electron-electron repulsion due to the Pauli exclusion principle is more important in determining molecular geometry than the electrostatic repulsion.[6] The number of electron pairs, therefore, determine the overall geometry that they will adopt. For example, when there are two electron pairs surrounding the central atom, their mutual repulsion is minimal when they lie at opposite poles of the sphere. Therefore, the central atom is predicted to adopt a linear geometry. If there are 3 electron pairs surrounding the central atom, their repulsion is minimized by placing them at the vertices of an equilateral triangle centered on the atom. Therefore, the predicted geometry is trigonal. Likewise, for 4 electron pairs, the optimal arrangement is tetrahedral.[4]
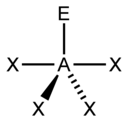
This overall geometry is further refined by distinguishing between bonding and nonbonding electron pairs. The bonding electron pair shared in a sigma bond with an adjacent atom lies further from the central atom than a nonbonding (lone) pair of that atom, which is held close to its positively-charged nucleus. VSEPR theory therefore views repulsion by the lone pair to be greater than the repulsion by a bonding pair. As such, when a molecule has 2 interactions with different degrees of repulsion, VSEPR theory offers the structure where lone pairs occupy positions that allow them to experience less repulsion. Lone pair-lone pair (lp-lp) repulsions are considered stronger than lone pair-bonding pair (lp-bp) repulsions, which in turn are considered stronger than bonding pair-bonding pair (bp-bp) repulsions, distinctions that then guide decisions about overall geometry when 2 or more non-equivalent positions are possible.[4] For instance, when 5 ligands or lone pairs surround a central atom, a trigonal bipyramidal molecular geometry is specified. In this geometry, the 2 collinear "axial" positions lie 180° apart from one another, and 90° from each of 3 adjacent "equatorial" positions; these 3 equatorial positions lie 120° apart from each other. The axial positions therefore experience more repulsion than the equatorial positions; hence, when there are lone pairs, they tend to occupy equatorial positions.[5]
The difference between lone pairs and bonding pairs may also be used to rationalize deviations from idealized geometries. For example, the H2O molecule has four electron pairs in its valence shell: two lone pairs and two bond pairs. The four electron pairs are spread so as to point roughly towards the apices of a tetrahedron. However, the bond angle between the two O-H bonds is only 104.5°, rather than the 109.5° of a regular tetrahedron, because the two lone pairs (whose density or probability envelopes lie closer to the oxygen nucleus) exert a greater mutual repulsion than the two bond pairs.[4][5]
AXE módszer
[szerkesztés]Az elmélet alkalmazásakor az elektronokat általában az AXE módszer szerint számoljuk. A a központi atomot jelöli, és mindig 1-es indexszel szerepel. X a ligandumok (az A-hoz kapcsolódó atomok) száma, E pedig a központi atom nemkötő elektronpárjainak száma.[4] X és E összege a sztérikus szám.
A sztérikus szám, valamint X és E értékeinek függvényében az elmélet az alábbi táblázat szerinti térszerkezetet jósolja. Megjegyzendő, hogy a térszerkezet neve csak az atomok, és nem az elektronok elrendeződését tükrözi – így például az AX2E1 V-alakja azt jelenti, hogy az AX2 három atomja nem egy egyenesre esik.
| Steric No. |
A molekula térszerkezete[7] 0 nemkötő pár |
A molekula térszerkezete[7] 1 nemkötő pár |
A molekula térszerkezete[7] 2 nemkötő pár |
A molekula térszerkezete[7] 3 nemkötő pár |
|---|---|---|---|---|
| 2 | ||||
| 3 |  |
 |
||
| 4 | 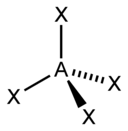 |
 |
 |
|
| 5 |  |
 |
 |
 |
| 6 |  |
 |
 |
|
| 7 |  |
 |
 |
|
| 8 | (TaF3−8)[5] |
|||
| 9 | Tricapped trigonal prismatic (ReH2−9)[10] OR Capped square antiprismatic[forrás?] |
| Molecule Type | Shape[7] | Electron arrangement†[7] | Geometry‡[7] | Examples |
|---|---|---|---|---|
| AX2E0 | lineáris | BeCl2,[1] HgCl2,[1] CO2[5] | ||
| AX2E1 | V-alakú | 
|

|
NO−2,[1] SO2,[7] O3,[1] CCl2 |
| AX2E2 | V-alakú | 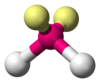
|

|
H2O,[7] OF2[11] |
| AX2E3 | lineáris | 
|
XeF2,[7] I−3,[12] XeCl2 | |
| AX3E0 | síkháromszöges | 
|

|
BF3,[7] CO2−3,[13] NO−3,[1] SO3[5] |
| AX3E1 | trigonális piramisos | 
|

|
NH3,[7] PCl3[14] |
| AX3E2 | T-alakú | 
|

|
ClF3,[7] BrF3[15] |
| AX4E0 | tetraéderes | 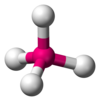
|

|
CH4,[7] PO3−4, SO2−4,[5] ClO−4,[1] TiCl4,[16] XeO4[17] |
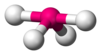
| AX4E1 | Seesaw | 
|
|
SF4[7] |
| AX4E2 | síknégyszöges | 
|

|
XeF4[7] |
| AX5E0 | trigonális bipiramisos | 
|

|
PCl5[7] |
| AX5E1 | tetragonális piramisos | 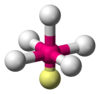
|

|
ClF5,[15] BrF5,[7] XeOF4[5] |
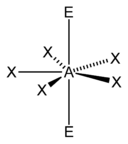
| AX5E2 | síkötszöges | 
|

|
XeF−5[9] |
| AX6E0 | oktaéderes | 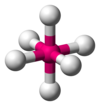
|

|
SF6,[7] WCl6[18] |
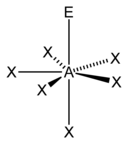
| AX6E1 | pentagonális piramisos | 
|

|
XeOF−5,[8] IOF2−5[8] |
| AX7E0 | pentagonális bipiramisos[5] | 
|

|
IF7[5] |
| AX8E0 | négyzetes antiprizmás[5] | 
|

|
IF−8, ZrF4−8, ReF−8 |
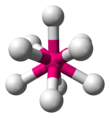
| AX9E0 | Tricapped trigonal prismatic (as drawn) OR capped square antiprismatic |
|

|
ReH2−9[10] |
Ha a központi atomhoz különböző (X) atom(ok) kapcsolódnak, a térszerkezet közelítőleg akkor is helyes, de a kötésszögek némileg változhatnak ahhoz képest, mintha a kapcsolódó atomok azonosak volnának. Például az alkének – mint a C2H4 – kettős kötésű szénatomja AX3E0, de a kötésszögek nem pontosan 120°-osak. Hasonló az AX3E1 szerkezetű SOCl2 is, mivel az X szubsztituensek nem egyformák, az XAX szögek sem mind egyenlőek.
As a tool in predicting the geometry adopted with a given number of electron pairs, an often used physical demonstration of the principle of minimal electron pair repulsion utilizes inflated balloons. Through handling, balloons acquire a slight surface electrostatic charge that results in the adoption of roughly the same geometries when they are tied together at their stems as the corresponding number of electron pairs. For example, five balloons tied together adopt the trigonal bipyramidal geometry, just as do the five bonding pairs of a PCl5 molecule (AX5) or the two bonding and three non-bonding pairs of a XeF2 molecule (AX2E3). The molecular geometry of the former is also trigonal bipyramidal, whereas that of the latter is linear.
Examples
[szerkesztés]The methane molecule (CH4) is tetrahedral because there are four pairs of electrons. The four hydrogen atoms are positioned at the vertices of a tetrahedron, and the bond angle is cos−1(−1⁄3) ≈ 109°28'.[19][20] This is referred to as an AX4 type of molecule. As mentioned above, A represents the central atom and X represents an outer atom.[4]
The ammonia molecule (NH3) has three pairs of electrons involved in bonding, but there is a lone pair of electrons on the nitrogen atom.[21] It is not bonded with another atom; however, it influences the overall shape through repulsions. As in methane above, there are four regions of electron density. Therefore, the overall orientation of the regions of electron density is tetrahedral. On the other hand, there are only three outer atoms. This is referred to as an AX3E type molecule because the lone pair is represented by an E.[4] By definition, the molecular shape or geometry describes the geometric arrangement of the atomic nuclei only, which is trigonal-pyramidal for NH3.[4]
Steric numbers of 7 or greater are possible, but are less common. The steric number of 7 occurs in iodine heptafluoride (IF7); the base geometry for a steric number of 7 is pentagonal bipyramidal.[5] The most common geometry for a steric number of 8 is a square antiprismatic geometry.[22] Examples of this include the octacyanomolybdate (Mo(CN)4−8) and octafluorozirconate (ZrF4−8) anions.[22]
The nonahydridorhenate ion (ReH2−9) in potassium nonahydridorhenate is a rare example of a compound with a steric number of 9, which has a tricapped trigonal prismatic geometry.[10][23] Another example is the octafluoroxenate ion (XeF2−8) in nitrosonium octafluoroxenate(VI),[9][24][25] although in this case one of the electron pairs is a lone pair, and therefore the molecule actually has a distorted square antiprismatic geometry.
Possible geometries for steric numbers of 10, 11, 12, or 14 are bicapped square antiprismatic (or bicapped dodecadeltahedral), octadecahedral, icosahedral, and bicapped hexagonal antiprismatic, respectively. No compounds with steric numbers this high involving monodentate ligands exist, and those involving multidentate ligands can often be analysed more simply as complexes with lower steric numbers when some multidentate ligands are treated as a unit.[26][27]
Kivételek
[szerkesztés]Néhány vegyületcsoport esetében az elmélet nem jól írja le a térszerkezetet.
Átmenetifémek vegyületei
[szerkesztés]
Számos átmenetifém-vegyület szerkezete nem egyezik meg az elmélet által jósolttal, ami annak tulajdonítható, hogy a vegyértékhéjon nincsenek nemkötő elektronpárok, de az atomtörzs d elektronjai és a ligandumok között kölcsönhatás lép fel.[28]
Egyes AX2E0 szerkezetű molekulák
[szerkesztés]A nehezebb alkáliföldfémek háromatomos halogenidjeinek (azaz az MX2 kalcium-, stroncium- és bárium-halogenidek) gázfázisú szerkezete – az elmélet által jósoltakkal szemben – nem lineáris, hanem V-alakú (a közelítő X-M-X kötésszögek: CaF2 145°; SrF2 120°; BaF2 108°; SrCl2 130°; BaCl2 115°; BaBr2 115°; BaI2 105°).[29] It has been proposed by Gillespie that this is caused by interaction of the ligands with the electron core of the metal atom, polarising it so that the inner shell is not spherically symmetric, thus influencing the molecular geometry.[28][30] Disilynes are also bent, despite having no lone pairs.[31]
Egyes AX2E2 szerkezetű molekulák
[szerkesztés]One example of the AX2E2 geometry is molecular lithium oxide, Li2O, a linear rather than bent structure, which is ascribed to its bonds being essentially ionic and the strong lithium-lithium repulsion that results.[32] Another example is O(SiH3)2 with an Si-O-Si angle of 144.1°, which compares to the angles in Cl2O (110.9°), (CH3)2O (111.7°), and N(CH3)3 (110.9°).[28] Gillespie and Robinson rationalize the Si-O-Si bond angle based on the observed ability of a ligand's lone pair to most greatly repel other electron pairs when the ligand electronegativity is greater than or equal to that of the central atom.[28] In O(SiH3)2, the central atom is more electronegative, and the lone pairs are less localized and more weakly repulsive. The larger Si-O-Si bond angle results from this and strong ligand-ligand repulsion by the relatively large -SiH3 ligand.[28]
Egyes AX6E1 és AX8E1 szerkezetű molekulák
[szerkesztés]
Some AX6E1 molecules, e.g. xenon hexafluoride (XeF6) and the Te(IV) and Bi(III) anions, TeCl2−6, TeBr2−6, BiCl3−6, BiBr3−6 and BiI3−6, are regular octahedra and the lone pair does not affect the geometry.[33] One rationalization is that steric crowding of the ligands allows no room for the non-bonding lone pair;[28] another rationalization is the inert pair effect.[34] Similarly, the octafluoroxenate anion (XeF2−8) is a square antiprism and not a distorted square antiprism (as predicted by VSEPR theory for an AX8E1 molecule), despite having a lone pair.
Odd-electron molecules
[szerkesztés]Sablon:Refimprove section The VSEPR theory can be extended to molecules with an odd number of electrons by treating the unpaired electron as a "half electron pair"—in effect, the odd electron has an influence on the geometry which is similar to a full electron pair, but less pronounced so that the geometry may be intermediate between the molecule with a full electron pair and the molecule with one less electron pair on the central atom.[forrás?] For example, nitrogen dioxide (NO2) is an AX2E0.5 molecule, with an unpaired electron on the central nitrogen; VSEPR predicts a geometry similar to the NO−2 ion (AX2E1, bent, bond angle approx. 120°), but intermediate between NO−2 and NO+2 (AX2E0, linear, 180°).[forrás?] In fact NO2 is bent with an angle of 134°, which is closer to 120° than to 180°, in qualitative agreement with the theory.[forrás?] Similarly chlorine dioxide (ClO2, AX2E1.5) has a geometry similar to ClO−2 but intermediate between ClO−2 and ClO+2.[forrás?]
Finally the methyl radical (CH3) is predicted to be trigonal pyramidal like the methyl anion (CH−3), but with a larger bond angle as in the trigonal planar methyl cation (CH+3). However in this case the VSEPR prediction is not quite true, as CH3 is actually planar, although its distortion to a pyramidal geometry requires very little energy.[35]
VSEPR and localized orbitals
[szerkesztés]The VSEPR theory places each pair of valence electrons in a bond or a lone pair found in a local region of the molecule. Molecular orbital (MO) theory yields a set of orbitals that have the symmetry of the molecule; some of these MO's may be delocalized over several atoms. However these orbitals can be transformed into an equivalent set of localized molecular orbitals.[36] In the water molecule for example, MO calculations yield two lone pairs—an s-p hybrid MO in the plane of the molecule and a pure p-type orbital perpendicular to the plane—that can be combined into two equivalent sp3 nonbonding orbitals comparable to the water oxygen lone pairs of VSEPR theory.[36] Likewise, there are two calculated bonding orbitals each extending over all three atoms, which can be combined into two localized orbitals, one for each bond. The delocalized and localized orbitals are generally described as providing completely equivalent descriptions of the ground state.[36]
Jegyzetek
[szerkesztés]- ↑ a b c d e f g Jolly, W. L.,Modern Inorganic Chemistry, McGraw-Hill, 1984, p.77-90. ISBN 0-07-032760-2
- ↑ Box, Vernon G. S. (1997. március 17.). „The Molecular Mechanics of Quantized Valence Bonds”. Journal of Molecular Modeling 3 (3), 124–141. o. DOI:10.1007/s008940050026. (Hozzáférés: 2011. szeptember 28.)
- ↑ H. Stephen Stoker. General, Organic, and Biological Chemistry. Cengage Learning, 119. o. (2009). ISBN 978-0-547-15281-3
- ↑ a b c d e f g h i j R.H. Petrucci, W.S. Harwood and F.G. Herring, General Chemistry (8th ed., Prentice-Hall 2002) pp.410-417. ISBN 0-13-014329-4
- ↑ a b c d e f g h i j k l m G.L. Miessler and D.A. Tarr, Inorganic Chemistry (2nd ed., Prentice-Hall 1999) pp.54-62. ISBN 0-13-841891-8
- ↑ R.J. Gillespie (2008), Coordination Chemistry Reviews vol.252, pp.1315-1327, Fifty years of the VSEPR model
- ↑ a b c d e f g h i j k l m n o p q r s Steric numbers 2-6 from R.H. Petrucci, W.S. Harwood and F.G. Herring, General Chemistry (8th ed., Prentice-Hall 2002) Table 11.1, pp.413-414. ISBN 0-13-014329-4
- ↑ a b c doi:10.1016/S0022-1139(99)00194-3
- ↑ a b c Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.498
- ↑ a b c Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.254
- ↑ Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.448
- ↑ Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.483
- ↑ Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.368
- ↑ Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.407
- ↑ a b Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.481
- ↑ Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.598-9
- ↑ Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.499
- ↑ Housecroft, C.E. and Sharpe A.G. "Inorganic Chemistry" (2nd edn, Pearson 2005. ISBN 0130-39913-2), p.659
- ↑ Valence Angle of the Tetrahedral Carbon Atom W.E. Brittin, J. Chem. Educ., 1945, 22 (3), p 145
- ↑ "Angle Between 2 Legs of a Tetrahedron" – Maze5.net
- ↑ R.H. Petrucci, W.S. Harwood and F.G. Herring, General Chemistry (8th ed., Prentice-Hall 2002) pp.392-393. ISBN 0-13-014329-4
- ↑ a b Inorganic Chemistry, Arnold Frederick Holleman, Academic Press, 1165. o. (2001). ISBN 0-12-352651-5
- ↑ Holleman, A. F.; Wiberg, E. "Inorganic Chemistry" Academic Press: San Diego, 2001. ISBN 0-12-352651-5.
- ↑ doi:10.1126/science.173.4003.1238
- ↑ Molecular origami: precision scale models from paper. University Science Books (1995). ISBN 0-935702-30-X
- ↑ Sablon:Holleman&Wiberg
- ↑ Sablon:Holleman&Wiberg
- ↑ a b c d e f Models of molecular geometry, Gillespie R. J., Robinson E.A. Chem. Soc. Rev., 2005, 34, 396–407, doi:10.1039/b405359c
- ↑ Chemistry of the Elements, 2nd, Butterworth-Heinemann (1997). ISBN 978-0-08-037941-8
- ↑ Core Distortions and Geometries of the Difluorides and Dihydrides of Ca, Sr, and Ba Bytheway I, Gillespie R.J, Tang T.H., Bader R.F. Inorganic Chemistry, 34,9, 2407–2414, 1995 doi:10.1021/ic00113a023
- ↑ Akira Sekiguchi, Rei Kinjo, Masaaki Ichinohe (2004. szeptember 1.). „A Stable Compound Containing a Silicon-Silicon Triple Bond”. Science 305 (5691), 1755–1757. o. DOI:10.1126/science.1102209. PMID 15375262.[1]
- ↑ A spectroscopic determination of the bond length of the LiOLi molecule: Strong ionic bonding, D. Bellert, W. H. Breckenridge, J. Chem. Phys. 114, 2871 (2001); doi:10.1063/1.1349424
- ↑ Wells A.F. (1984) Structural Inorganic Chemistry 5th edition Oxford Science Publications ISBN 0-19-855370-6
- ↑ Sablon:Housecroft2nd
- ↑ Anslyn E.V. and Dougherty D.A., Modern Physical Organic Chemistry (University Science Books, 2006), p.57
- ↑ a b c IN Levine, 1991, "Quantum Chemistry," 4th Ed., New York:Prentice-Hall, sec.15.8. The two descriptions are equivalent because the total wavefunction for all electrons is a Slater determinant, which is unchanged by the transformation of the orbitals.
Fordítás
[szerkesztés]Ez a szócikk részben vagy egészben a VSEPR theory című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
További olvasnivalók
[szerkesztés]- Chemistry: Foundations and Applications. J. J. Lagowski, ed. New York: Macmillan, 2004. ISBN 0-02-865721-7. Volume 3, pages 99–104.
- 3D Chem - Chemistry, Structures, and 3D Molecules
- IUMSC - Indiana University Molecular Structure Center
Kapcsolódó szócikkek
[szerkesztés]- Bent's rule (effect of ligand electronegativity)
- Linear combination of atomic orbitals
- Molecular geometry
- Molecular modelling
- Software for molecular modeling
- Valency interaction formula

