Schulze-módszer

A Schulze-módszer egy hely betöltésére kiírt szavazási rendszer. A módszer más neveken is ismert, mint Schwartz szekvenciális csöpögtetés (SSD), Cloneproof Schwartz szekvenciális csöpögtetés, és még számos más néven. Több szervezet is használja, például a Wikipédia, a Debian, a Gentoo fejlesztőközössége, a Svéd Kalózpárt és a Német Kalózpárt. Többségi, többségi vesztes, kölcsönös többségi, Condorcet, Condorcet-vesztes, Smith tulajdonságú, monoton, klónfüggetlen, visszafejthető, és fordítottan szimmetrikus.

Tulajdonságai

Teljesülő tulajdonságok

A Schulze-módszer megfelel ezeknek a tulajdonságoknak:

• Korlátozatlan tartomány, minden szavazónak megengedett az összes preferenciasorrend
• Minden összesített preferenciasorrend előfordulhat (Arrow lehetetlenségi tétele)
• Diktátormentesség
• Pareto hatékony
• Monoton
• Többségi kritérium
• Többségi vesztes kritérium
• Condorcet kritérium
• Condorcet vesztes kritérium
• Schwartz-kritérium
• Smith-kritérium
• A Smith-dominált alternatívák függetlensége
• Kölcsönösségi többségi kritérium
• A klónok függetlensége
• Fordított szimmetria
• Mono-append
• Mono-add-plump
• Visszakövethetőségi kritérium
• Polinomiális bonyolultság
• prudence
• MinMax halmazok
• Woodall sokféleségi kritérium a szigorú megelőzés esetén
• Szimmetria-komplemencia a gyenge megelőzés esetén

Nem teljesülő tulajdonságok

Mivel a Schulze-módszer Condorcet tulajdonságú, ezért nem teljesíti a következőket:

• Részvételi kritérium
• Konzisztencia
• Védettség az összebeszélés ellen
• Védettség a süllyesztés ellen
• Visszahatásmentesség

A diktátormentesség miatt, és mert az egyöntetű szavazás esetén a végeredmény megegyezik az egyöntetű szavazatok eredményével, ezért Arrow tételéből következően

• Az irreleváns alternatívák függetlensége

A Schulze-módszer nem teljesíti a

• Peyton Young-kritériumot

Első lépés

Minden szavazólap tartalmazza a jelöltek teljes listáját. A szavazók sorrendet állítansak fel a jelöltek között szimpátiájuk alapján. A legjobb kapja az 1-es, a második legjobb a 2-es számot, és így tovább.

A szavazónak lehetősége van:

• több jelöltnek is ugyanazt a preferenciát adni

Nem állít fel sorrendet közöttük.

• preferenciákat kihagyni

Ez nem befolyásolja a szavazás eredményét, mert csak a sorrend a fontos.

• jelölteket kihagyni

A kihagyott jelöltekről felteszik, hogy a szavazó a többi jelölt mögé sorolja, és nem állít fel közöttük sorrendet.

Második lépés

Minden jelöltpárra kiszámítják, hogy hányan helyezik az egyiket szigorúan a másik elé. Ha V és W jelöltek, akkor rájuk ez a szám d[V,W].

Harmadik lépés

Definíciók:

Ha X és Y jelöltek, akkor egy z erősségű X-től Y-ig vezető út jelöltek egy C(1),...,C(n) sorozata, ahol:

• C(1) megegyezikX-szel
• C(n) megegyezik Y-nal
• d[C(i),C(i+1)] > d[C(i+1),C(i)] minden i = 1,...,(n-1)-re
• [C(i),C(i+1)] ≥ z minden i = 1,...,(n-1)-re.

p[A,B] a legerősebb A-ból B-be vezető út ereje.

Ha nincs az A és a B jelöltek között út, akkor p[A,B] : = 0.

A D jelölt jobb, mint E, ha p[D,E] > p[E,D].

D Schulze-győztes, ha p[D,E] ≥ p[E,D] minden más E-be helyettesíthető jelöltre.

Belátható, hogy a jobb tulajdonság tranzitív, ezért biztosan van győztes.

Példák

Első példa

21 szavazó, 4 jelölt:

8 ACDB

2 BADC

4 CDBA

4 DBAC

3 DCBA

A páronkénti legyőzte mátrix a következő:

	d[*,A]	d[*,B]	d[*,C]	d[*,D]
d[A,*]		8	14	10
d[B,*]	13		6	2
d[C,*]	7	15		12
d[D,*]	11	19	9

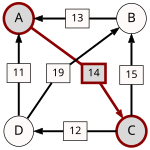
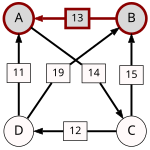
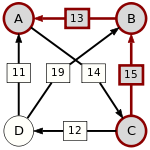
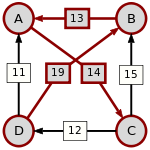
A páronkénti legyőzte gráf:

Egy út ereje a leggyengébb láncszemének erejével egyezik meg. Az alábbi táblázat minden jelöltpárra megadja a legerősebb utat. A leggyengébb láncszemek aláhúzással vannak megjelölve.

A legerősebb utak:

	... A-ba	... B-be	... C-be	... D-be
A-ból ...		A-(14)-C-(15)-B	A-(14)-C	A-(14)-C-(12)-D
B-ből ...	B-(13)-A		B-(13)-A-(14)-C	B-(13)-A-(14)-C-(12)-D
C-ből ...	C-(15)-B-(13)-A	C-(15)-B		C-(12)-D
D-ből ...	D-(19)-B-(13)-A	D-(19)-B	D-(19)-B-(13)-A-(14)-C

A legerősebb utak ereje:

	p[*,A]	p[*,B]	p[*,C]	p[*,D]
p[A,*]		14	14	12
p[B,*]	13		13	12
p[C,*]	13	15		12
p[D,*]	13	19	13

A D jelölt Schulze-győztes, mert p[D,X] ≥ p[X,D] minden más X jelöltre.

• 14 = p[A,B] > p[B,A] = 13, az A jelölt jobb, mint a B jelölt.
• 14 = p[A,C] > p[C,A] = 13, az A jelölt jobb, mint a C jelölt.
• 15 = p[C,B] > p[B,C] = 13, a C jelölt jobb, mint a B jelölt.
• 13 = p[D,A] > p[A,D] = 12, a D jelölt jobb, mint az A jelölt.
• 19 = p[D,B] > p[B,D] = 12, a D jelölt jobb, mint a B jelölt.
• 13 = p[D,C] > p[C,D] = 12, a D jelölt jobb, mint a C jelölt.

Ezért a Schulze-rangsor is D > A > C > B.

Második példa

45 szavazó dönt 5 jelöltről:

• 5 $ACBED$
• 5 $ADECB$
• 8 $BEDAC$
• 3 $CABED$
• 7 $CAEBD$
• 2 $CBADE$
• 7 $DCEBA$
• 8 $EBADC$

Először a páronkénti preferenciákat számítják ki. Például $A$ és $B$ közül $5+5+3+7=20$ részesítette előnyben $A$-t, és $8+2+7+8=25$ $B$-t.

Irányított gráf a d[*, *] preferenciákkal címkézve

A páronkénti preferenciák mátrixa

	d[*,A]	d[*,B]	d[*,C]	d[*,D]	d[*,E]
d[A,*]		20	26	30	22
d[B,*]	25		16	33	18
d[C,*]	19	29		17	24
d[D,*]	15	12	28		14
d[E,*]	23	27	21	31

A d[X, Y] értékek közül világoszöldek a győztesek, vagyis azok, amelyekre d[X, Y] > d[Y, X], a többiek háttere rózsaszín. A végső győztes még nem látszik a páronkénti adatok alapján.

A második lépésben meghatározzuk a legerősebb utakat. A gráf csak azokat az éleket tartalmazza, amelyekre d[X, Y] > d[Y, X], vagyis a győztes éleket. Az ellenkező irányú és előjelű vesztes éleket mellőztük.

Például a B és D közötti legerősebb út ereje p[B, D] = 33, mivel a kettő közötti él a legerősebb út, és ereje 33. De A és C esetén már nem a közvetlen él a legerősebb, hiszen (A, D, C) ereje 28 szemben az AC él 26-ával szemben. Az út ereje megegyezik leggyengébb élének erejével.

A következő táblázat tartalmazza az összes jelöltpárra a legerősebb utat, aláhúzással jelölve a leggyengébb éleket:

A legerősebb utak

	... A-ba	... B-be	... C-be	... D-be	... E-be
A-ból ...		A-(30)-D-(28)-C-(29)-B	A-(30)-D-(28)-C	A-(30)-D	A-(30)-D-(28)-C-(24)-E	A-ból ...
B-ből ...	B-(25)-A		B-(33)-D-(28)-C	B-(33)-D	B-(33)-D-(28)-C-(24)-E	B-ből ...
C-ből ...	C-(29)-B-(25)-A	C-(29)-B		C-(29)-B-(33)-D	C-(24)-E	C-ből ...
D-ből ...	D-(28)-C-(29)-B-(25)-A	D-(28)-C-(29)-B	D-(28)-C		D-(28)-C-(24)-E	D-ből ...
E-ből ...	E-(31)-D-(28)-C-(29)-B-(25)-A	E-(31)-D-(28)-C-(29)-B	E-(31)-D-(28)-C	E-(31)-D		E-ből ...
	... A-ba	... B-be	... C-be	... D-be	... E-be

A legerősebb utak ereje

	p[*,A]	p[*,B]	p[*,C]	p[*,D]	p[*,E]
p[A,*]		28	28	30	24
p[B,*]	25		28	33	24
p[C,*]	25	29		29	24
p[D,*]	25	28	28		24
p[E,*]	25	28	28	31

Most már megadható a végeredmény is. Például összehasonlítva A-t és B-t A jobb, mint B, mert 28 = p[A,B] > p[B,A] = 25. E jobb, mint D, mivel 31 = p[E,D] > p[D,E] = 24. Tovább folytatva E > A > C > B > D a végső erősorrend, és a győztes E. Más szavakkal, p[E,X] ≥ p[X,E] minden más X jelöltre.

Manipulálás

A szavazás manipulálásának egy módja az esélyesek szétválasztása. Ha a jelöltek között két esélyes van, P és Q, akkor a P-t választók hajlamosak arra, hopgy P-t helyezzék az élre, és Q-t a lista végére. Ezzel az őszinte választáshoz képest megnövelik $p[P,Q]$-t, és csökkentik $p[Q,P]$-t. Jelöljön E a következőkben egy tetszőleges jelöltet a többi közül! Ekkor $p[P,E]$ és $p[E,Q]$ nő, és $p[E,P]$ vagy $p[Q,E]$ csökken.

Ez a stratégia megnöveli az így szavazók szavazatának súlyát az őszinte szavazókkal szemben; növeli P esélyét, és csökkenti Q esélyét. Ha a két jelölt támogatottsága nagyjából megegyezik, és mindkét jelölt támogatói ezt a módszert használják, akkor a hatások nagyjából kiegyenlítik egymást.

Mivel a szavazók átrendezik szavazataikat, ezért a végső sorrend nem az őszinte véleményt fogja tükrözni. Ha a végén lesz Condorcet-győztes, akkor semmi sem garantálja azt, hogy ez a jelölt minden más jelöltet legyőzne, ha csak kettejük közül lehetne választani, mivel a páronkénti rangok nem az őszinte véleményt tükrözik.

Ha nem két, hanem több esélyes jelölt van, akkor a manipuláció egy módosított változata továbbra is működik. Itt egy jelöltet sorolnak az élre, és a többi esélyest a sor legvégére. Ez erősíti a szavazat súlyát, de azt eredményezi, hogy egy máskülönben teljesen esélytelen jelölt nyer, akit mindenki a sor végére tenne, ha őszintén szavazna. Ez minden, a Condorcet-módszeren alapuló szavazási rendszert érint. Ez a manipuláció felveti a fogolydilemmát.

Implementáció

A Schulze-módszer implementálásakor csak a legerősebb út erejének kiszámítása a nehéz. Ez egy jól ismert gráfelméleti probléma, mégpedig a legszélesebb út problémája. Ez megoldható a Floyd–Warshall-algoritmus egy változatával, aminek pszeudokódja:

# Input: d[i,j], hány szavazó részesíti előnyben i-t j-vel szemben.
# Output: p[i,j], a legerősebb ij út ereje.

for i from 1 to C
   for j from 1 to C
      if (i ≠ j) then
         if (d[i,j] > d[j,i]) then
            p[i,j] := d[i,j]
         else
            p[i,j] := 0

for i from 1 to C
   for j from 1 to C
      if (i ≠ j) then
         for k from 1 to C
            if (i ≠ k and j ≠ k) then
               p[j,k] := max ( p[j,k], min ( p[j,i], p[i,k] ) )

Az algoritmus bonyolultsága C³ , ahol C a jelöltek száma. Ez nem foglalja magába a d[*,*] értékek kiszámítását, amit naivan implementálva a bonyolultság C² szorozva a szavazók számával.

Holtversenyek és alternatív implementációk

Ha a szavazók több jelöltnek is adhatják ugyanazt a preferenciát, akkor a végeredmény függhet d[*,*] definíciójától. A két természetes választás előírhat szigorú vagy gyenge preferenciát. Mindazonáltal mindkét esetben a Schulze-rangsorban nem lesznek körök, és ha a d[*,*] számok mind különböznek, akkor holtverseny sem lehet, a sorrend és a győztes egyértelmű.

Habár nem szeretik, hogy több jelöltnek ugyanaz lehet a preferenciája (mivel rendszerint jóval több a szavazó, mint a jelölt), mégis lehetséges ilyen kimenetel. Schulze cikkében azt javasolta, hogy egy véletlenül választott elektor törje meg ezt az egyöntetűséget, és ezt ismételjük, amíg kell.

A módszer több nevét egy alternatív implementáció után kapta:

1. Rajzoljunk fel egy teljes irányított gráfot az összes jelölttel
2. Alkalmazzuk felváltva a következő két lépést:

• Töröljük azokat a jelölteket, amelyekből nem érhető el az összes többi
• Töröljük el a leggyengébb élt

1. Az utoljára maradt jelölt a győztes.

Ez az implementáció azonban lassabb.

Története

Markus Schulze 1997-ben dolgozta ki a módszert. Nyilvános levelezőlistákon vitatták meg 1997–1998-ban és 2000-ben. Ezután sok közösségben bevezették, például a Software in the Public Interest (2003), Debian (2003), Gentoo (2005), TopCoder (2005) Wikimedia (2008), KDE (2008), the Free Software Foundation Europe (2008), a Svéd Kalózpárt (2009), és a Német Kalózpárt (2010). A francia Wikipédiában a két több jelöltes módszer egyikeként már 2005-ben bevezették, és többször használták.

2011-ben Schulze publikálta módszerét a Social Choice and Welfare. szaklapban.

További információk

A Wikimédia Commons tartalmaz Schulze-módszer témájú médiaállományokat.

• Proposed Statutory Rules for the Schulze Single-Winner Election Method by Markus Schulze
• A New Monotonic, Clone-Independent, Reversal Symmetric, and Condorcet-Consistent Single-Winner Election Method by Markus Schulze