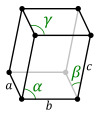
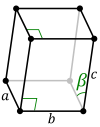
Primitív cella

A kristálytanban és a szilárdtestfizikában primitív cellának nevezzük a minimális méretű elemi cellát. A primitív cellák tehát a kristályrács elemi építőkövei, azok a legkisebb alakzatok, melyekből megfelelő transzlációs műveletekkel az egész kristályrács felépíthető.
Jellemzői
[szerkesztés]A primitív cella egyben elemi cella is, így belőle megfelelő transzlációs lépésekkel a kristályrács felépíthető. Például egy háromdimenziós rácsban megadhatók az primitív bázisvektorok, melyek egyrészt kifeszítenek egy paralelepipedon alakú térfogatot (mely primitív cella), másrészt velük a rács bármely transzlációs vektora kifejezhető:
,
ahol transzlációs vektor, és egész számok bármely értékére a transzlációs vektor a rácsot önmagába viszi.
Egy adott rács esetén általában többféleképpen megadható a primitív cella, de ezek térfogata a definíció értelmében megegyezik egymással. A primitív bázisvektorokkal kifejezhető az általuk kifeszített paralelepipedon térfogata, mely a fentiek szerint az adott rácshoz tartozó összes primitív cella térfogatával megegyezik:
.
Az elemi cellák esetében általában úgy számolják a cellához tartozó pontok számát, hogy minden rácspontot elosztanak annyifelé, ahogy cella osztozik rajtuk. Azaz ha egy rácspont két cellához is tartozik, mindkét cellában fél-fél rácspontként veszik figyelembe. Az elemi cellákhoz általában tartozhat egy, vagy több rácspont is, de a primitív cellákhoz a rácsnak csak egyetlen rácspontja tartozik.[1]
A primitív cella egy speciális esete a Wigner–Seitz-cella, mely a szomszédos rácspontokat összekötő szakaszok felezőmerőlegesei által határolt térfogat.
Kétdimenziós primitív cella
[szerkesztés]Kétdimenziós rácsban a primitív cella választható úgy, hogy paralelogramma legyen. Speciális esetekben szögei lehetnek derékszögűek, oldalai pedig páronként, vagy mind azonosak.
 paralelogramma(Monoklin) paralelogramma(Monoklin)
|
 rombusz(Ortorombos) rombusz(Ortorombos)
|
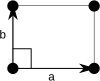 téglalap(ortorombos) téglalap(ortorombos)
|
 négyzet(tetragonális) négyzet(tetragonális)
|
Háromdimenziós primitív cella
[szerkesztés]Egy háromdimenziós rácsban a primitív rácsvektorok paralelepipedon térfogatot feszítenek ki, melynek jellemzői alapján a rács kategorizálható. Speciális esetekben a paralelepipedon egyes szögei megegyezhetnek, illetve egyes oldalak páronként vagy mind azonosak lehetnek.
Jegyzetek
[szerkesztés]- ↑ DoITPoMS - TLP Library Crystallography - Unit Cell (angol nyelven). www.doitpoms.ac.uk. (Hozzáférés: 2017. március 27.)
Források
[szerkesztés]- Sólyom Jenő: A modern szilárdtest-fizika alapjai I: Szerkezet és dinamika. Budapest: ELTE Eötvös Kiadó. 2009. ISBN 9789632840970
- Charles Kittel: Bevezetés a szilárdtest-fizikába. Budapest: Műszaki Könyvkiadó. 1981.
Fordítás
[szerkesztés]Ez a szócikk részben vagy egészben a Primitive cell című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.