Wigner–Seitz-cella

A szilárdtestfizikában a Wigner–Seitz-cella egy speciális primitív cella, a Voronoj-cellák koncepciójának alkalmazása kristályok esetére. Nevét Wigner Jenőről és Frederick Seitzről kapta.

A kristályokban az atomok rendezett háromdimenziós szerkezetet alkotnak, leírásukra kristályrácsot alkalmazhatunk. A rács rendelkezik diszkrét transzlációs szimmetriával, mely azt jelenti, hogy találhatók olyan vektorok (illetve ezek egész többszörösei), melyek mentén való eltolással a rács önmagával fedésbe hozható.

Az ilyen periodikus szerkezetek kristálytani leírásban primitív cellának nevezzük azt a térfogatot, mely a kristály legkisebb ismétlődő eleme, azaz pusztán egy rácspontot tartalmaz. A primitív cellát általában többféleképpen is megválaszthatjuk, melynek egy lehetséges módja a Wigner–Seitz-cella. Egy rácspont körüli Wigner–Seitz-cellához azok a pontok tartoznak, melyek a térben az összes rácspont körül éppen ehhez vannak a legközelebb.

A szilárdtestfizikában a reciprokrácsban, hullámszámtérben megadható Wigner–Seitz-cellát az adott pont körüli Brillouin-zónának nevezzük.

Definíció

Egy rácspont körüli Wigner–Seitz-cella azon pontok halmaza a térben, melyek a rácspontok közül az adott ponthoz vannak a legközelebb. Ennek a tartománynak a meghatározásához a Dirichlet-féle szerkesztést alkalmazhatjuk.

Matematikailag belátható, hogy a Wigner–Seitz-cella valóban primitív cella, ugyanis egyetlen rácsponthoz tartozik és ha a transzlációs szimmetria mentén eltolva minden rácspontban felrajzoljuk, akkor ezek a cellák az egész teret hézagmentesen fedik.

Reciproktérben a Wigner–Seitz-cella jelöli ki az első Brillouin-zónát, mely a szilárdtestek sávelméletének egy fontos része. A Brillouin-zóna segítségével, sok elektromos jellemző mellett például megadható az is, hogy az adott anyag fémes, félvezető, vagy szigetelő lesz.

A cella szerkesztése

A Wigner–Seitz-féle primitív cella szerkesztése síkbeli trigonális rács egy rácspontja körül.

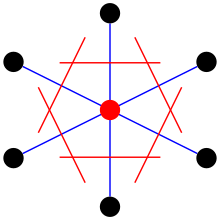
Egy rácspont körüli Wigner–Seitz-cellát úgy szerkeszthetjük meg, hogy az adott rácspontból egyenes szakaszokat húzunk tetszőleges (célszerűen a közeli, azaz első szomszéd, másodszomszéd, stb.) rácspontokig. Minden szakaszon megszerkesztjük a szakaszok felező merőlegeseit (két dimenzióban a szakaszfelezők merőleges egyenesek, három dimenzióban pedig merőleges síkok lesznek). A szakaszfelezők által, a rácspont körül bezárt lehető legkisebb térfogat lesz a Wigner–Seitz-cella. Ez a cella adott rács esetén egyértelműen meghatározható. A Wigner–Seitz-cella egyben primitív cella is, azaz olyan minimális térfogatú cella, mellyel a rács hézagmentesen lefedhető.

Matematikai háttér

A Wigner–Seitz-cella matematikai hátterét a Voronoj-cellák adják. A Voronoj-cellák például egy síkbeli ponthalmaz esetében a sík olyan hézagmentes felosztását (faktorizálását) jelentik, amikor minden ponthoz az a területet rendeljük, melynek pontjai az adott ponthalmazbeli ponthoz legközelebb esnek.

Fordítás

Ez a szócikk részben vagy egészben a Wigner–Seitz cell című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.