Origón átmenő egyenes

Origón átmenő egyenesek az euklideszi síkban

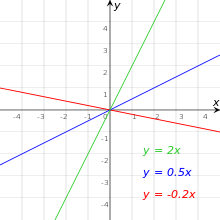
A matematikában az origón átmenő egyenes egy olyan egyenes, ami átmegy egy adott Descartes-féle koordináta-rendszer origóján. Leírhatók a többi egyenesnél egyszerűbb egyenlettel, egyenes arányossággal. Vektorterekben ezek az egyenesek éppen a vektortér egydimenziós alterei.

A síkban

Definíció

A euklideszi síkban egy origón átmenő egyenes egy egyenes, ami áthalad a koordináta-rendszer origóján, tehát a $(0,0)$ ponton. Az egyenes egyenlete koordináta formában

$ax+by=0$

ahol $a$ és $b$ paraméterek, melyek közül legfeljebb csak egy lehet nulla. Ha $b\neq 0$, akkor az egyenlet egyszerűbb formára hozható:

$y=mx$

ahol $m=-{\tfrac {a}{b}}$ az egyenes meredeksége. A $b\neq 0$ kikötés miatt az $x$ tengelyre merőleges origón átmenő egyenes, tehát az $y$ tengely egyenlete nem hozható erre a formára.

Példák

Fontos példák a koordinátatengelyek, melyek egyenlete:

$y=0$   és   $x=0$.

További fontos példák az I. és III., illetve a II. és IV. síknegyed felezői, melyek egyenletei:

$x-y=0$   és   $x+y=0$.

Vektoregyenletek

Az origón átmenő egyenesek is leírhatók vektoregyenletekkel. Paraméteres alakban egy origón átmenő egyenes a síknak azokat a pontjait tartalmazza, melyekre

${\vec {x}}=s{\vec {u}}$

ahol $s\in \mathbb {R}$. Egy origón átmenő egyenes pontjainak helyvektorai mind skalárszorosai az ${\vec {u}}$ irányvektornak. Az egyenlet normálformája

${\vec {n}}\cdot {\vec {x}}=0$

ahol az ${\vec {n}}$ vektor az egyenes egy normálvektora, és ${\vec {n}}\cdot {\vec {x}}$ az ${\vec {n}}$ vektor és egy ${\vec {x}}$ vektor skalárszorzata. Tehát az egyenes a sík olyan pontjaiból áll, melyeknek helyvektorai ortogonálisak az ${\vec {n}}$ normálvektorra.

Merőleges egyenes

Minden origón átmenő egyeneshez létezik rá merőleges, origón átmenő egyenes. Ennek az origóhoz tartozó talpponti egyenesnek az egyenlete

$bx-ay=0$

illetve, ha ez nem az $y$ tengely, vagyis $m\neq 0$, akkor

$y=-{\frac {1}{m}}x$.

A kiindulási egyenes egy normálvektora az origóhoz, mint talpponthoz tartozó talpponti egyenesének irányvektora.

A térben

Origón átmenő egyenes háromdimenziós térben

Definíció

Az origón átmenő egyenesek magasabb dimenziós euklideszi terekben is leírhatók vektoregyenletekkel. Paraméteres alakban egy origón átmenő egyenes az ${\vec {u}}\in \mathbb {R} ^{n}$ irányvektorral a tér azon ${\vec {x}}\in \mathbb {R} ^{n}$ pontjaiból áll, melyekre

${\vec {x}}=s{\vec {u}}$

ahol $s\in \mathbb {R}$. Tehát egy origón átmenő egyenes a térnek azokból a pontjaiból áll, melyek helyvektorai az irányvektor skalárszorosai. Normálegyenlettel azonban a 2-nél magasabb dimenziós terekben azonban nem egyenest, hanem hipersíkot lehet leírni.

Példák

Háromdimenziós térben a koordinátatengelyek egyenletei:

${\vec {x}}=s{\vec {e}}_{1},{\vec {x}}=s{\vec {e}}_{2}$   és   ${\vec {x}}=s{\vec {e}}_{3}$

ahol $s\in \mathbb {R}$, és ${\vec {e}}_{1}=(1,0,0)$, ${\vec {e}}_{2}=(0,1,0)$ és ${\vec {e}}_{3}=(0,0,1)$ a standard egységvektorok.

Pont távolsága

Egy ${\vec {v}}$ irányvektorral adott pont távolsága egy origón átmenő ${\vec {u}}$ irányvektorú egyenestől $|{\vec {v}}-{\vec {p}}|$, ahol

${\vec {p}}={\frac {{\vec {v}}\cdot {\vec {u}}}{{\vec {u}}\cdot {\vec {u}}}}\,{\vec {u}}$

a talppont helyvektora, ami megegyezik a ${\vec {v}}$ merőleges vetületével az egyenesre.

Vektortér struktúra

Egy euklideszi tér vektorai vektorteret alkotnak, ez az úgynevezett koordinátatér. Egy origón átmenő egyenes pontjainak helyvektorai ennek egy alterét alkotják.

$U=\{{\vec {x}}\in \mathbb {R} ^{n}\mid {\vec {x}}=s{\vec {u}}~{\text{ahol}}~s\in \mathbb {R} \}$.

Ez pontosan megegyezik az egyenes ${\vec {u}}$ irányvektorának lineáris burkával. Ezzel az origón átmenő egyenesek éppen a tér egydimenziós alterei.

Előállítás metszetként

Origón átmenő egyenes origón átmenő síkok metszeteként

Egy háromdimenziós tér kétdimenziós alterei pontosan az origón átmenő síkok. Két különböző origón átmenő sík metszeteként origón átmenő egyenes adódik, melynek egy ${\vec {u}}$ irányvektora

${\vec {u}}={\vec {n}}_{1}\times {\vec {n}}_{2}$,

ahol ${\vec {n}}_{1}$ és ${\vec {n}}_{2}$ a síkok normálvektorai. Általában az $(n-1)$ alterek origón átmenő hipersíkok, és $n-1$ ilyen hipersík, melyeknek normálvektorai rendre ${\vec {n}}_{1},\ldots ,{\vec {n}}_{n-1}$, metszetként azt az origón átmenő egyenest adja, aminek irányvektora n-dimenziós általánosított vektoriális szorzással:

${\vec {u}}={\vec {n}}_{1}\times \cdots \times {\vec {n}}_{n-1}$

Források

• Kenneth Eriksson, Donald Estep, Claes Johnson. Angewandte Mathematik: Body and Soul 1. Springer (2006) 
• Mike Scherfner, Torsten Volland. Mathematik für das erste Semester. Springer (2012) 

Fordítás

Ez a szócikk részben vagy egészben az Ursprungsgerade című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.