Mediángráf

Három csúcs mediánja egy mediángráfban

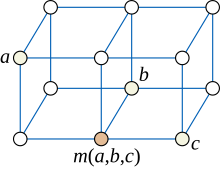
A matematika, azon belül a gráfelmélet területén egy mediángráf (median graph) olyan irányítatlan gráf, melynek tetszőlegesen választott a, b, c csúcsa egyedi mediánnal rendelkezik: a statisztikában ismert medián alatt gráfokban olyan m(a,b,c) csúcs értendő, amely része az a, b és c csúcspárjai közötti mindhárom legrövidebb útnak.

A mediángráfok tanulmányozása már régóta tart, az első fecskék közé tartozik (Birkhoff & Kiss 1947) vagy (explicitebben) (Avann 1961) tanulmánya, de a „mediángráf” kifejezés először (Nebeský 1971)-nél jelent meg. Ahogy Chung, Graham és Saks írja, „a mediángráfok természetes módon felbukkannak a rendezett halmazok és diszkét disztributív hálók tanulmányozásakor, kiterjedt irodalmuk van”. A filogenetikus rendszertanban a maximális parszimóniájú leszármazási fákat megtestesítő Buneman-gráf is egy mediángráf. A mediángráfok a választáselméletben is előbukkannak: ha alternatívák egy halmaza mediángráf-szerkezetű, lehetséges az alternatívák közötti többségi preferencia egyértelmű meghatározása.

A mediángráfok további áttekintését adják: (Klavžar & Mulder 1999), (Bandelt & Chepoi 2008) és (Knuth 2008).

Példák

Egy fa három csúcsának mediánja, a csúcsok közti legrövidebb utak uniója által alkotott részfa közepén.

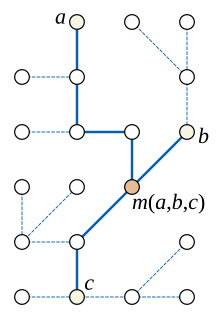
Minden fa mediángráf. Ennek belátásához vegyük észre, hogy egy fában az a, b és c csúcsok alkotta párok közötti három legrövidebb út uniója vagy maga is egy út, vagy egy három fokszámú csúcsban találkozó három út által alkotott részfa. Az első esetben, tehát ha az utak uniója is egy út, akkor az m(a,b,c) medián megegyezik a, b vagy c közül azzal, amelyik a másik két csúcs közötti úton helyezkedik el. A második esetben, ha az utak uniója alkotta részfa nem egy út, akkor a medián a részfa középponti helyzetű, három fokszámú csúcsa.

A fákon kívül mediángráfok még a rácsgráfok is. Egy rácsgráfban az m(a,b,c) medián koordinátái megegyeznek az a, b és c csúcsok koordinátáinak mediánjával. Megfordítva, bármely mediángráf csúcsai címkézhetők rácspontokkal úgy, hogy a mediánok az előbb említett módon koordinátákkal számíthatók legyenek.

Egy négyszöggráf.

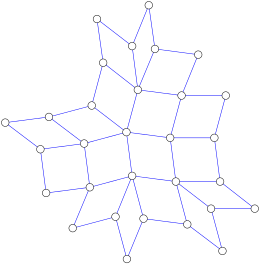
A négyszöggráfok szintén a mediángráfok közé tartoznak; ezek olyan síkgráfok, melyekben az összes belső tartomány négyszög alakú és minden belső csúcs négy vagy több éllel érintkezik. Egy poliominó a négyszöggráfok speciális esete, ezért mindig mediángráfot alkot.

Tetszőleges G irányítatlan gráf szimplexgráfja, κ(G) minden csúcsa a G egy-egy klikkjének (teljes részgráfjának) felel meg; a κ(G) két csúcsát akkor köti össze él, ha a megfelelő klikkek G egy csúcsával térnek el. A szimplex gráf minden esetben mediángráf, melyben bármely klikkhármas mediánja a többségi szabály alapján meghatározható, kiválasztva hogy a klikkek melyik csúcsait tartalmazza.

A négy hosszúságú körgráfon kívül egy körgráf sem lehet mediángráf. Az ilyen körgráfokban mindig kiválaszthatók úgy az a, b és c csúcsok, hogy a három legrövidebb út megkerülje a teljes kört anélkül, hogy lenne közös metszetük. Az ilyen csúcshármasoknak pedig nincs mediánjuk.

Ekvivalens meghatározások

Egy gráf tetszőleges két csúcsa, a és b közötti élek minimális számát a csúcsok távolságának nevezzük, jelölése d(a,b). Az a és b közötti legrövidebb utakon található csúcsok intervallumát így definiáljuk:

I(a,b) = {v | d(a,b) = d(a,v) + d(v,b)}.

A mediángráf definíciója alapján bármely három a, b és c csúcsához tartozó intervallumok egyetlen pontban metszik egymást:

Minden a, b és c-re |I(a,b) ∩ I(a,c) ∩ I(b,c)| = 1.

Ekvivalens definíció szerint bármely három a, b és c csúcshoz található olyan m(a,b,c) csúcs, amire a gráfban a súlyozatlan különbségek kielégítik a következő egyenlőtlenségeket:

• d(a,b) = d(a,m(a,b,c)) + d(m(a,b,c),b)
• d(a,c) = d(a,m(a,b,c)) + d(m(a,b,c),c)
• d(b,c) = d(b,m(a,b,c)) + d(m(a,b,c),c)

és m(a,b,c) az egyetlen csúcs, amire ez igaz.

A mediángráfok előállnak még 2-kielégíthetőségi problémák megoldáshalmazaként, hiperkockagráfok retrakciójával, véges medián algebrák gráfjaiként, Helly-féle split rendszerek Buneman-gráfjaiként és a 2 windexű gráfokként; lásd az alábbi szakaszokat.

Disztributív hálók és mediánalgebrák

Disztributív háló gráfja, Hasse-diagram formájában lerajzolva.

A hálóelmélet területén egy véges háló gráfjának csúcsait a háló elemei alkotják, két csúcs között pedig akkor húzódik él, ha a hozzájuk tartozó elemek a hálóban fedési relációban vannak. A hálók szemléltetése gyakran Hasse-diagramjukkal történik, melyek a hálók gráfjainak lerajzolásai. Ezek a gráfok, különösen a disztributív hálók esetében, a mediángráfok közeli rokonai.

Egy disztributív hálóban Birkhoff a következőképpen definiálta az önduális, háromváltozós medián műveletet:

m(a,b,c) = (a ∧ b) ∨ (a ∧ c) ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) ∧ (b ∨ c),

ami kielégít egyes axiómákat, amiket a 0 és 1 közötti számok szokásos mediánja, általánosabban pedig a mediánalgebrák is kielégítenek:

• Idempotencia: m(a,a,b) = a minden a-ra és b-re.
• Kommutativitás: m(a,b,c) = m(a,c,b) = m(b,a,c) = m(b,c,a) = m(c,a,b) = m(c,b,a) bármely a, b, c hármasra.
• Disztributivitás: m(a,m(b,c,d),e) = m(m(a,b,e),c,m(a,d,e)) bármely a, b, c, d, e ötösre.
• Neutrális elemek: m(0,a,1) = a minden a-ra.

A disztributivitás követelménye felcserélhető az asszociativitással:

• Asszociativitás: m(x,w,m(y,w,z)) = m(m(x,w,y),w,z)

A mediánképzés művelete segítségével definiálható egyfajta intervallum a disztributív hálókon:

I(a,b) = {x | m(a,x,b) = x} = {x | a ∧ b ≤ x ≤ a ∨ b}.

Egy véges disztributív háló gráfjában a és b csúcsok közt akkor húzódik él, ha I(a,b) = {a,b}. Ennek a gráfnak bármely a és b csúcspárjára a fent hálóelméleti kifejezésekkel meghatározott I(a,b) intervallum az a-ból b-be vezető legrövidebb utakon lévő csúcsokból áll, így egybeesik a korábban gráfelméleti alapokon definiált intervallumokkal. Bármely a, b és c hálóelemre az m(a,b,c) a három intervallum, I(a,b), I(a,c) és I(b,c) egyedi metszetét alkotja. Ezért bármely véges disztributív háló gráfja mediángráf. Megfordítva, ha egy G mediángráfban létezik két olyan, 0-val és 1-gyel jelölt csúcs, melyek közötti legrövidebb úton az összes többi csúcs megtalálható (ekvivalens megfogalmazásban m(0,a,1) = a minden a-ra), akkor definiálható az a disztributív háló, melyben a ∧ b = m(a,0,b) és a ∨ b = m(a,1,b), G pedig ennek a hálónak a gráfja lesz.

(Duffus & Rival 1983) a disztributív hálók gráfjait úgy karakterizálja, mint hiperkockák átmérőt megtartó retrakcióit. Általánosabban, minden mediángráfban meghatározható egy m ternáris művelet idempotenciával, kommutativitással és disztributivitással, igaz, potenciálisan egy disztributív háló neutrális elemeit nélkülözve. Bármely véges halmazon értelmezett ternáris művelet, ami rendelkezik ezzel a három tulajdonsággal (de nem feltétlenül vannak 0 és 1 elemei) ugyanilyen módon egy mediángráfot határoz meg.

Konvex halmazok és Helly-családok

Mediángráfban egy S csúcshalmazt akkor tekintünk konvexnek, ha az S-be tartozó bármely a és b csúcsára igaz, hogy az I(a,b) intervallum összessége az S részhalmaza. Ekvivalens megfogalmazásban, az intervallumokra fent adott két definíció alapján S akkor konvex, ha bármely két csúcsa közötti összes legrövidebb utat tartalmazza, vagy ha tartalmazza minden olyan ponthármas mediánját, melynek legalább két pontja S-beli. Észrevehető, hogy bármely két konvex halmaz metszete is konvex.

A mediángráf konvex halmazai Helly-tulajdonságúak: ha F egymást páronként metsző konvex halmazok tetszőleges családja, akkor F összes halmazának is van nem üres közös metszete. Hiszen, ha F csak három konvex halmazzal rendelkezik, legyenek ezek S, T és U, az S és T metszete legyen a, a T és U metszete legyen b, az S és U metszete pedig legyen c, akkor a konvexitás miatt minden a és b közötti legrövidebb útnak T-n belül kell lennie, és hasonlóan a másik két pár közötti útnak is a megfelelő két halmazban kell lennie; de m(a,b,c) mindhárom pár közötti útba beletartozik, tehát mindhárom halmaz része, így a közös metszetet alkotja. Ha F-nek háromnál több konvex halmaza van, akkor a halmazok számára vonatkozó indukcióval látható be az állítás; hiszen bármely F-beli halmazpárt felcserélve a metszetükkel, a halmazhármasokra való eredményt felhasználva igazolható, hogy a lecserélt család továbbra is páronként metszésben van.

A mediángráfok konvex halmazainak egy különösen fontos, az euklideszi terek féltereihez hasonló szerepet játszó családja, a

W_uv = {w | d(w,u) < d(w,v)}

a gráf minden uv éléhez meghatározott halmazokból áll. Magyarán W_uv azokból a csúcsokból áll, melyek közelebb állnak u-hoz mint v-hez, vagy ekvivalens megfogalmazás szerint azok a w csúcsok, melyekre a v-ből w-be vezető legrövidebb utak közül legalább egy u-n megy keresztül. Annak megmutatásához, hogy W_uv konvex, legyen w₁w₂...w_k tetszőleges, W_uv-n belül kezdődő és ott is végződő legrövidebb út; ekkor w₂ szintén W_uv-n belül található, különben a csúcsok közti lehetséges távolságok figyelme vételével megmutatható lenne, hogy a két pont, m₁ = m(u,w₁,w_k) és m₂ = m(m₁,w₂...w_k) az u, w₁ és w_k különböző mediánjai lennének, ami ellentmond a mediángráf definíciójának, ami megköveteli a mediánok egyediségét. Ezért a W_uv két csúcsa közötti legrövidebb úton minden egymást követő csúcs is W_uv-beli, ezért W_uv-nek tartalmaznia kell a csúcsok közötti összes legrövidebb utat, ami éppen a konvexitás egyik definíciója.

A W_uv halmazok Helly-tulajdonsága fontos szerepet játszik a mediángráfok 2-kielégíthetőségi kifejezésekként való karakterizálásában, lásd lejjebb.

2-kielégíthetőség (2-SAT)

A mediángráfok közeli kapcsolatban állnak a 2-kielégíthetőségi problémák megoldáshalmazaival, aminek segítségével jellemezni lehet ezeket a gráfokat, továbbá kapcsolatba hozhatók hiperkockák szomszédságtartó leképezéseivel.

Egy 2-kielégíthetőségi kifejezés logikai változók és ún. „klózok” (a változópárokon értelmezett megkötések, melyek megkövetelik egyes értékkombinációk elkerülését) gyűjteményéből áll. Az ilyen problémákat általában konjunktív normálformában fejezik ki, melyben az egyes klózok diszjunkcióként szerepelnek, a megkötések összessége pedig klózok konjunkciójaként van felírva, például a következő formában:

$(x_{11}\lor x_{12})\land (x_{21}\lor x_{22})\land \cdots \land (x_{n1}\lor x_{n2})\land \cdots .$

Egy ilyen kifejezés megoldásában olyan igazságértékek vannak hozzárendelve a változókhoz, melyek az összes klózt kielégítik, tehát a konjunktív normálformájú kifejezésbe behelyettesítve őket a kifejezés igaz értéket kap. Az összes megoldás családjának természetes szerkezete egy mediánalgebra, ahol három megoldás mediánja úgy kapható meg, hogy minden igazságérték a három megoldás értékeiből többségi függvénnyel képzett értéket veszi fel; könnyen ellenőrizhető, hogy ez a medián megoldás nem sértheti meg egyetlen klózt sem. Ezért a megoldások mediángráfot alkotnak, melyben egy megoldás szomszédja megkapható változók olyan halmazának negálásával, melyeknek egymással egyenlőnek vagy ellentétesnek kell lenniük a megkötések alapján.

Megfordítva, minden G mediángráf kifejezhető egy 2-SAT kifejezés megoldáshalmazaként. Ez a reprezentáció előállítható úgy, hogy a 2-kielégíthetőségi kifejezés minden változó a gráf egy élének orientációját írja le, és az egyes megkötések két élnek akkor engedik meg, hogy közös orientációpárral rendelkezzenek, ha létezik olyan v csúcs, melyre mindkét orientáció a más csúcsokból v-be vezető legrövidebb utak mentén fekszik. Minden G-beli v csúcs megfelel a 2-kielégíthetőségi kifejezés olyan megoldásának, ahol minden él irányítása v felé mutat. A kifejezés minden megoldásának valamely v csúcs felől kell jönnie, ahol v a közös metszete a w-ből u-ba irányított élek W_uw halmazai közös metszetének; ez a közös metszet a W_uw halmazok Helly-tulajdonsága miatt létezik. Tehát, ennek a 2-SAT kifejezésnek a megoldásai kölcsönösen megfeleltethetők G csúcsainak.

Hiperkockák összehúzottjai

Egy kocka összehúzása hat csúcsból álló részgráfjába.

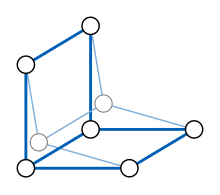
Egy G gráf összehúzottja vagy retrakciója (retraction) egy szomszédságtartó leképezés G-ből annak valamely részgráfjába. Precízebben fogalmazva olyan, G-t saját magába átvivő φ homomorfizmus, melyre φ(v) = v a φ(G) részgráf minden v csúcsára. A retrakció képét G egy összehúzottjának nevezzük. A retrakciók a nemexpanzív leképezések közé tartoznak: a φ(v) és φ(w) közti távolság bármely v és w-re legfeljebb a v és w közti távolsággal egyezik meg, és az egyenlőség akkor áll fenn, ha v és w is a φ(G)-be tartozik. Ebből következik, hogy a retrakció G izometrikus részgráfja: az összehúzottban szereplő távolságok megegyeznek a G-beliekkel.

Ha G mediángráf, a, b és c pedig a φ(G) összehúzott tetszőleges három csúcsa, akkor φ(m(a,b,c)) szükségképpen a, b és c egy mediánja, ezért megegyezik m(a,b,c)-vel. Tehát φ(G) tartalmazza minden csúcshármasának mediánját, így szintén mediángráf. Más szavakkal, a mediángráfok családja a retrakció műveletére nézve zárt.

Egy hiperkockagráf csúcsai az összes lehetséges k-bites bináris vektornak felelnek meg, élei pedig az egyetlen bitben eltérő bináris vektorokat kötik össze; a hiperkockagráfok a k dimenziós rácsgráfok speciális esetei, ezért mediángráfok. Az a, b, c bináris vektor mediánja meghatározható a, b, c minden egyes bithelyiértékén a többségi függvény értékének kiszámításával. Mivel a mediángráfok a retrakció műveletére zártak, és a mediángráfok közé tartoznak a hiperkockagráfok, ezért a hiperkockagráfok minden összehúzása is mediángráf lesz.

Megfordítva, minden mediángráf előállítható hiperkockagráf retrakciójával. Ez jól látható a mediángráfok és a 2-SAT kifejezések közötti, fent leírt kapcsolatból is: legyen G egy 2-SAT kifejezés megoldásainak gráfja; az általánosság megsértése nélkül feltehető, hogy a kifejezés úgy van megadva, hogy nincs benne olyan változópáros, melyek minden megoldásban mindig egyenlők vagy mindig ellentétes értékűek. Ekkor a kifejezés összes igazságérték-hozzárendeléseinek tere hiperkockát alkot. A két változónak vagy a két változó komplementerének diszjunkciójából alkotott minden 2-SAT kifejezésbeli klózhoz megalkotható a hiperkocka olyan összehúzása, melyben a klózt megsértő igazságértékek hozzárendelődnek azokhoz, melyekben mindkét változó kielégíti a klózt, anélkül, hogy a hozzárendelés többi változója megváltozna. A klózonként a leírt módon megkomponált retrakciók a hiperkocka a kifejezés megoldásterébe való retrakcióját adják, így előállítják G-t egy hiperkocka összehúzottjaként. A mediángráfok hiperkockák izometrikus részgráfjai, más néven parciális kockák. Nem minden parciális kocka mediángráf; például a hat csúcsból álló körgráf parciális kocka, de nem mediángráf.

(Imrich & Klavžar 2000) módszere alapján egy mediángráf hiperkockába történő izometrikus beágyazása O(m log n) időben megszerkeszthető, ahol n és m a gráf csúcsainak, illetve éleinek a száma.

Háromszögmentes gráfok és felismerési algoritmusok

Háromszögmentes gráf átalakítása mediángráffá.

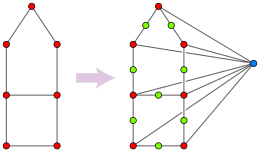
Annak tesztelése, hogy egy gráf mediángráf, illetve hogy egy gráf háromszögmentes gráf-e, egyaránt jól tanulmányozott problémák. (Imrich, Klavžar & Mulder 1999) észrevétele alapján a két probléma bizonyos értelemben számítási bonyolultság szempontjából ekvivalens. Ezért a háromszögmentesség tesztelésére ismert legjobb korlát, O(m^1,41), a mediángráfok tesztelésének is korlátot szab, és a mediángráf-tesztelő algoritmusok bármely továbbfejlesztése a háromszögtesztelő algoritmusok javulásához is elvezetne.

Az egyik irányból tegyük fel, hogy a bemenetül kapott G gráfnak a háromszögmentességét kell vizsgálnunk. Konstruáljunk G-ből egy új H gráfot, melynek csúcsai G-nek 0, 1 vagy 2 szomszédú csúcsainak halmazából adódnak. Két ilyen halmaz akkor szomszédos H-ban, ha pontosan egy csúcsban különböznek. H ezzel egyenértékű, az ábrán is látható meghatározása szerint úgy kapható meg, hogy G minden élét két élből álló úttá bontjuk fel, majd hozzáadunk egy új csúcsot, ami G minden eredeti csúcsához csatlakozik. Ez a H gráf a konstrukció módja miatt parciális kocka, de csak akkor mediángráf, ha G háromszögmentes: ugyanis ha a, b és c G-ben háromszöget alkotnak, akkor {a,b}, {a,c} és {b,c} nem rendelkezik H-beli mediánnal, mivel egy ilyen mediánnak az {a,b,c} háromszögnek kellene megfelelnie, de G három vagy több csúcsból álló halmazai nem alkotnak csúcsokat H-ban. Épp ezért G pontosan akkor háromszögmentes, ha H mediángráf. Amennyiben G háromszögmentes, H az ő szimplexgráfja. A H mediángráf-tesztelése megtörténhet az előbbi konstrukció alapján, G háromszögmentességét vizsgálva. Ez a transzformáció megtartja a probléma számítási bonyolultságát, mivel H mérete G-ével arányos.

Az ellenkező irányba, a háromszögteszttől a mediántesztig történő redukció némileg komplikáltabb, és a korábbi (Hagauer, Imrich & Klavžar 1999)-féle mediángráf-felismerő algoritmust igényli, ami a mediángráfok több szükséges feltételét teszteli közel lineáris időben. Az új kulcslépés egy szélességi keresés, ami egy tetszőlegesen kiválasztott gyökér-csúcstól való távolság alapján szintekre particionálja a gráf csúcsait, majd a szintekből egy-egy gráf létrehozása, melyekben két csúcs akkor szomszédos, ha az előző szinten közös az ősük; végül ezekben a gráfokban háromszögek keresése. Minden ilyen háromszög mediánjának a három csúcs közös ősének kell lennie; ha ilyen közös ős nem létezik, a gráf nem mediángráf. Ha minden megtalált háromszögnek van mediánja, és a korábbi algoritmus alapján a mediángráfok többi szükséges feltételét is teljesíti a gráf, akkor tényleg mediángráf. Az algoritmushoz nem csak a háromszögek létezését kell tesztelni, hanem ténylegesen meg is kell találni egy-egy szint gráfjának az összes háromszögét. Egy általános gráfban a legrosszabb esetben a háromszögek listázásához Ω(m^3/2) időre is szükség lehet, azonban Hagauer et al. megmutatták, hogy a szintfelbontáskor kapott gráfok háromszögeinek száma közel lineáris, ami lehetővé teszi az Alon et al.-féle gyors mátrixszorzási technika használatát a háromszögkeresésre.

Leszármazási fák, Buneman-gráfok és Helly-féle split rendszerek

Öt különböző fajta egér Buneman-gráfja.

A filogenezis feladata a fajok megfigyelt jellemzőiből az evolúciós törzsfa vagy törzsfák meghatározása; egy törzsfában a fajok különböző csúcsokon találhatók, ezen kívül lehetnek további „rejtett csúcsok”, de ezeknek a rejtett csúcsoknak három vagy éllel kell érintkezniük, és karakterisztikákkal kell őket címkézni. Egy karakterisztika akkor „bináris”, ha csak két különböző értéket vehet fel, és a fajok és karakterisztikáik egy halmaza akkor rendelkezik perfekt filogenezissel, ha létezik olyan evolúciós törzsfa, melyben a karakterisztikus értékekkel címezett csúcsok (fajok és rejtett csúcsok) folytonos részfát alkotnak. Ha nem lehetséges perfekt filogenezist létrehozni, gyakran a kitűzött cél a maximális parszimónia elérése, ami azt is jelenti, hogy minimalizálni kell az eltérések számát a fa éleinek végpontjain lévő valamely karakterisztika szerint, az összes élre és karakterisztikára összegezve.

(Buneman 1971) megadott egy módszert a bináris karakterisztikák alapján a perfekt filogenezis meghatározására, amennyiben az létezik. Módszere természetes módon általánosítható tetszőleges faj és bináris karakterisztika halmazából a mediángráf megalkotására, amit „mediánhálózatnak” vagy „Buneman-gráfnak” neveznek és a filogenetikus hálózatok egy fajtája. Minden maximális parszimóniájú törzsfa beágyazható a Buneman-gráfba, abban az értelemben, hogy a fa élei a gráfban lévő utakat követik, a fa éleken történő karakterisztika-értékváltások száma pedig megegyezik a gráfban lévő út hasonló számával. A Buneman-gráf pontosan akkor fa, ha létezik perfekt filogenezis; ez akkor történik, ha nincs olyan inkompatibilis karakterisztika-pár, melyben a karakterisztikus értékek mind a négy kombinációja előfordul.

Adott fajok és karakterisztikák halmazából a Buneman-gráf előállításához először ki kell küszöbölni a többi fajtól nem megkülönböztethető, redundáns fajokat és az olyan redundáns karakterisztikákat, melyek mindig megegyeznek valamely más karakterisztikával. Ezután vegyünk fel egy-egy rejtett csúcsot minden ismert faj karakterisztikus tulajdonságai mindkét lehetséges értékének kombinációjához. Az ábra példájában vannak kisméretű, barna, farkatlan egerek; kis, ezüstszínű, farkatlan egerek; kis, barna, nem farkatlan egerek; nagy, barna, nem farkatlan egerek és nagy, ezüstszínű, nem farkatlan egerek. A Buneman-gráf módszerét követve ilyenkor létrehoznánk egy rejtett csúcsot, ami az ismeretlen kis, ezüstszínű, nem farkatlan egérfajt jelöli, mivel minden páronkénti kombináció (kicsi és ezüstszínű, kicsi és nem farkatlan, ezüstszínű és nem farkatlan) megfigyelhető valamely ismert fajban. A módszer azonban nem következtetne a nagy barna farkatlan egerek létezésére, mivel egyetlen egérben sem figyelték meg egyszerre a nagy méret és a farkatlanság vonásait. A rejtett csúcsok meghatározása után az egyetlen karakterisztikában különböző fajok vagy rejtett csúcsok között kell behúzni az éleket.

A bináris karakterisztikák gyűjteménye leírható ún. „split rendszerként” (split system) is, azaz olyan halmazcsaládként, melyekben a család minden halmazának komplementer halmaza is a család része. Ez a split rendszer minden karakterisztikus értékhez egy-egy halmazzal rendelkezik, mely tartalmazza az adott értéket felvevő fajokat. Ha a rejtett csúcsokat is figyelembe vesszük, a split rendszer Helly-tulajdonságú: minden páronként metsző részcsaládnak van közös metszete is. Bizonyos értelemben a mediángráfok karakterizálhatók úgy is, hogy Helly-split rendszerekből állnak elő: a mediángráf uv éleihez meghatározott (W_uv, W_vu) párok Helly-féle split rendszert alkotnak, tehát ezen a rendszeren Buneman-gráfkonstrukciót alkalmazva nem lesz szükség rejtett csúcsokra és az eredmény újra a kiindulási gráf lesz.

(Bandelt et al. 1995) és (Bandelt, Macaulay & Richards 2000) leírnak néhány technikát a Buneman-gráf egyszerűsített kézi kiszámítására, és bemutatják, hogyan használható ez a konstrukció az humángenetikai kapcsolatok vizualizációjára.

További tulajdonságok

A gráfok Descartes-szorzata művelet két kisebb mediángráfból nagyobb mediángráfot hoz létre.

• Két mediángráf Descartes-szorzata egy harmadik mediángráf lesz. A szorzatgráf mediánjai kiszámíthatók a két tényező mediánjaiból, ahogy a rácsgráfok mediánjai is előállíthatók az egyes lineáris dimenziók mediánjának független megkeresésével.
• Egy gráf windex-e meghatározza, mennyi look-ahead-re („előretekintésre”) van szükség annak a problémának optimális megoldásához, melyben megadják a gráf csúcsainak s_i sorozatát és kimenetként meg kell adni azt a t_i csúcssorozatot, melyben a távolságok összege, d(s_i,t_i) és d(t_i − 1,t_i) minimális. A mediángráfok pontosan azok a gráfok, melyek windex értéke 2. Egy mediángráfban az optimális választás a következő: t_i = m(t_i − 1,s_i,s_i + 1).
• A medián egyediségét mint tulajdonságot „egyedi Steiner-pont tulajdonságnak” (unique Steiner point property) is nevezik. Egy mediángráf három csúcsára, a, b, illetve c-re vonatkozó optimális Steiner-fa megtalálható az a-ból, b-ből és c-ből az m(a,b,c)-be vezető legrövidebb utak uniójaként. (Bandelt & Barthélémy 1984) általánosabban vizsgálták adott csúcshalmaz egyes csúcsaiba vezető minimális úthosszal rendelkező csúcs megkeresésének problémáját, megmutatva, hogy mediángráfban bármely, páratlan számosságú csúcshalmazra egyedi eredményt ad. Azt is megmutatták, hogy mediángráfban ennek az S csúcshalmaznak a mediánja kielégíti a választásokon használt Condorcet-kritériumot: bármely más csúcshoz képest közelebb van az S csúcsainak többségéhez.
• Ahogy az a parciális kockákra általában is igaz, az n csúcsú mediángráfok éleinek száma is legfeljebb (n/2) log₂ n lehet. Az élek számát azonban túlságosan lecsökkenteni sem lehet: (Klavžar, Mulder & Škrekovski 1998) igazolták, hogy minden mediángráfra fennáll a 2n − m − k ≤ 2 egyenlőtlenség, ahol m az élek száma, k pedig a hiperkocka dimenziója, melyből a mediángráf összehúzható. Az egyenlőség pontosan akkor áll fenn, ha a mediángráf nem tartalmaz kockákat. Ez a mediángráfokra vonatkozó másik azonosság következménye: Σ (−1)^dim(Q) Euler-karakterisztika értéke mindig egy, ahol az összegzés az adott mediángráf összes Q hiperkocka-részgráfján történik.
• A mediángráfok közül kizárólag azok regulárisak, melyek hiperkockák.
• Minden mediángráf moduláris gráf. A moduláris gráfok olyan gráfosztályt alkotnak, melynek tagjaiban bármely három csúcs renddelkezik mediánnal, de ez a medián nem feltétlenül egyedi.

Fordítás

• Ez a szócikk részben vagy egészben a Median graph című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

• Alon, Noga; Yuster, Raphael & Zwick, Uri (1995), "Color-coding", Journal of the ACM 42 (4): 844–856, DOI 10.1145/210332.210337.
• Avann, S. P. (1961), "Metric ternary distributive semi-lattices", Proceedings of the American Mathematical Society (American Mathematical Society) 12 (3): 407–414, DOI 10.2307/2034206.
• Bandelt, Hans-Jürgen (1984), "Retracts of hypercubes", Journal of Graph Theory 8 (4): 501–510, DOI 10.1002/jgt.3190080407.
• Bandelt, Hans-Jürgen & Barthélémy, Jean-Pierre (1984), "Medians in median graphs", Discrete Applied Mathematics 8 (2): 131–142, DOI 10.1016/0166-218X(84)90096-9.
• Bandelt, Hans-Jürgen & Chepoi, Victor (2008), "Metric graph theory and geometry: a survey", Surveys on Discrete and Computational Geometry, vol. 453, Contemporary Mathematics, Providence, RI: American Mathematical Society, pp. 49–86, doi:10.1090/conm/453/08795.
• Bandelt, Hans-Jürgen; Forster, P. & Sykes, B. C. et al. (October 1, 1995), "Mitochondrial portraits of human populations using median networks", Genetics 141 (2): 743–753, <http://www.genetics.org/cgi/content/abstract/141/2/743>.
• Bandelt, Hans-Jürgen; Forster, P. & Rohl, Arne (January 1, 1999), "Median-joining networks for inferring intraspecific phylogenies", Molecular Biology and Evolution 16 (1): 37–48, doi:10.1093/oxfordjournals.molbev.a026036, <http://mbe.oxfordjournals.org/cgi/content/abstract/16/1/37>.
• Bandelt, Hans-Jürgen; Macaulay, Vincent & Richards, Martin B. (2000), "Median networks: speedy construction and greedy reduction, one simulation, and two case studies from human mtDNA", Molecular Phylogenetics and Evolution 16 (1): 8–28, DOI 10.1006/mpev.2000.0792.
• Barthélémy, Jean-Pierre (1989), "From copair hypergraphs to median graphs with latent vertices", Discrete Mathematics 76 (1): 9–28, DOI 10.1016/0012-365X(89)90283-5.
• Barthélemy, J.-P.; Leclerc, B. & Monjardet, B. (1986), "On the use of ordered sets in problems of comparison and consensus of classifications", Journal of Classification 3 (2): 187–224, DOI 10.1007/BF01894188.
• Birkhoff, Garrett & Kiss, S. A. (1947), "A ternary operation in distributive lattices", Bulletin of the American Mathematical Society 53 (1): 749–752, doi:10.1090/S0002-9904-1947-08864-9, <http://projecteuclid.org/euclid.bams/1183510977>.
• Buneman, P. (1971), "The recovery of trees from measures of dissimilarity", in Hodson, F. R.; Kendall, D. G. & Tautu, P. T., Mathematics in the Archaeological and Historical Sciences, Edinburgh University Press, pp. 387–395.
• Chepoi, V.; Dragan, F. & Vaxès, Y. (2002), "Center and diameter problems in planar quadrangulations and triangulations", Proc. 13th ACM-SIAM Symposium on Discrete Algorithms, pp. 346–355, <http://portal.acm.org/citation.cfm?id=545381.545427>.
• Chepoi, V.; Fanciullini, C. & Vaxès, Y. (2004), "Median problem in some plane triangulations and quadrangulations", Computational Geometry: Theory & Applications 27: 193–210, DOI 10.1016/j.comgeo.2003.11.002.
• Chiba, N. & Nishizeki, T. (1985), "Arboricity and subgraph listing algorithms", SIAM Journal on Computing 14: 210–223, DOI 10.1137/0214017.
• Chung, F. R. K.; Graham, R. L. & Saks, M. E. (1987), "Dynamic search in graphs", in Wilf, H., Discrete Algorithms and Complexity (Kyoto, 1986), vol. 15, Perspectives in Computing, New York: Academic Press, pp. 351–387, <http://www.math.ucsd.edu/~fan/mypaps/fanpap/98dynamicsearch.pdf>.
• Chung, F. R. K.; Graham, R. L. & Saks, M. E. (1989), "A dynamic location problem for graphs", Combinatorica 9 (2): 111–132, doi:10.1007/BF02124674, <http://www.math.ucsd.edu/~fan/mypaps/fanpap/101location.pdf>.
• Day, William H. E. & McMorris, F. R. (2003), Axiomatic Consensus Theory in Group Choice and Bioinformatics, Society for Industrial and Applied Mathematics, pp. 91–94, ISBN 0-89871-551-2.
• Dress, A.; Hendy, M. & Huber, K. et al. (1997), "On the number of vertices and edges of the Buneman graph", Annals of Combinatorics 1 (1): 329–337, DOI 10.1007/BF02558484.
• Dress, A.; Huber, K. & Moulton, V. (1997), "Some variations on a theme by Buneman", Annals of Combinatorics 1 (1): 339–352, DOI 10.1007/BF02558485.
• Duffus, Dwight & Rival, Ivan (1983), "Graphs orientable as distributive lattices", Proceedings of the American Mathematical Society (American Mathematical Society) 88 (2): 197–200, DOI 10.2307/2044697.
• Feder, T. (1995), Stable Networks and Product Graphs, vol. 555, Memoirs of the American Mathematical Society.
• Hagauer, Johann; Imrich, Wilfried & Klavžar, Sandi (1999), "Recognizing median graphs in subquadratic time", Theoretical Computer Science 215 (1–2): 123–136, DOI 10.1016/S0304-3975(97)00136-9.
• Hell, Pavol (1976), "Graph retractions", Colloquio Internazionale sulle Teorie Combinatorie (Roma, 1973), Tomo II, vol. 17, Atti dei Convegni Lincei, Rome: Accad. Naz. Lincei, pp. 263–268.
• Imrich, Wilfried & Klavžar, Sandi (1998), "A convexity lemma and expansion procedures for bipartite graphs", European Journal of Combinatorics 19 (6): 677–686, DOI 10.1006/eujc.1998.0229.
• Imrich, Wilfried & Klavžar, Sandi (2000), Product Graphs: Structure and Recognition, Wiley, ISBN 0-471-37039-8.
• Imrich, Wilfried; Klavžar, Sandi & Mulder, Henry Martyn (1999), "Median graphs and triangle-free graphs", SIAM Journal on Discrete Mathematics 12 (1): 111–118, DOI 10.1137/S0895480197323494.
• Itai, A. & Rodeh, M. (1978), "Finding a minimum circuit in a graph", SIAM Journal on Computing 7 (4): 413–423, DOI 10.1137/0207033.
• Jha, Pranava K. & Slutzki, Giora (1992), "Convex-expansion algorithms for recognizing and isometric embedding of median graphs", Ars Combinatoria 34: 75–92.
• Klavžar, Sandi & Mulder, Henry Martyn (1999), "Median graphs: characterizations, location theory and related structures", Journal of Combinatorial Mathematics and Combinatorial Computing 30: 103–127.
• Klavžar, Sandi; Mulder, Henry Martyn & Škrekovski, Riste (1998), "An Euler-type formula for median graphs", Discrete Mathematics 187 (1): 255–258, DOI 10.1016/S0012-365X(98)00019-3.
• Klavžar, Sandi & Škrekovski, Riste (2000), "On median graphs and median grid graphs", Discrete Mathematics 219 (1-3): 287–293, DOI 10.1016/S0012-365X(00)00085-6.
• Knuth, Donald E. (2008), "Median algebras and median graphs", The Art of Computer Programming, vol. IV, Fascicle 0: Introduction to Combinatorial Algorithms and Boolean Functions, Addison-Wesley, pp. 64–74, ISBN 978-0-321-53496-5.
• Mulder, Henry Martyn (1980), "n-cubes and median graphs", Journal of Graph Theory 4 (1): 107–110, DOI 10.1002/jgt.3190040112.
• Mulder, Henry Martyn & Schrijver, Alexander (1979), "Median graphs and Helly hypergraphs", Discrete Mathematics 25 (1): 41–50, DOI 10.1016/0012-365X(79)90151-1.
• Nebeský, Ladislav (1971), "Median graphs", Commentationes Mathematicae Universitatis Carolinae 12: 317–325.
• Škrekovski, Riste (2001), "Two relations for median graphs", Discrete Mathematics 226 (1): 351–353, DOI 10.1016/S0012-365X(00)00120-5.
• Soltan, P.; Zambitskii, D. & Prisăcaru, C. (1973), Extremal problems on graphs and algorithms of their solution, Chişinău: Ştiinţa.

További információk

• Median graphs, Information System for Graph Class Inclusions.
• Network, Free Phylogenetic Network Software. Network generates evolutionary trees and networks from genetic, linguistic, and other data.
• PhyloMurka, open-source software for median network computations from biological data.