Klotoid

Ha a kormányt állandó sebességgel forgatják, az autó klotoid pályát ír le.

A klotoid (clothoid, clothoide) - más néven Cornù-féle spirál vagy Euler-féle spirál - olyan síkgörbe, aminek $P$ pontbeli $g$ görbülete egyenesen arányos az O kezdőponttól mért $s={\widehat {OP}}$ ívhosszal: $g=a\cdot s$ .

A síkon egyenletes sebességgel haladó jármű akkor mozog klotoid pályán, ha a vezető a jármű volánját egyenletesen forgatja el. Ekkor a megtett úttal arányosan csökken a pálya simulókörének sugara, tehát az $R\cdot s=a$ fordított arányosság is jellemzi a görbét.

Elnevezése

A görög mitológiából ismert három párka egyike Klothon (Κλωθών). Neve a klothein (κλωθείν) = gombolyítani jelentésű görög szóból eredeztethető. A párkák a mítosz szerint az élet fonalának gombolyítói, s a klotoid a gombolyagra emlékeztető alakjáról kapta a nevét. Az irodalomban használt más elnevezései a görbe analízisében jelentős eredményeket elérő két tudósra utalnak:

• Leonard Euler (1707-1783) svájci matematikus a harmonikus oszcillátor vizsgálatához,
• Marie Alfred Cornù (1841-1902) francia fizikus a fény diffrakciós vizsgálatának tanulmányozásához, a Fresnel-integrálok grafikus ábrázolása során konstruálta a görbét.

Leírása

A balra kanyarodó spirált a

$P(t)=(x,\;y)=(k\cdot C(t),\;k\cdot S(t))$,

a jobbra kanyarodót a

$P(t)=(x,\;y)=(k\cdot S(t),\;k\cdot C(t))$,

paraméteres egyenletek írják le,

ahol:

a paraméter értelmezési tartománya: $(-\infty <t<+\infty )$,

$k$: a görbe méretét meghatározó hasonlósági együttható,

a két Fresnel-integrál:

$C(x)=\int _{0}^{x}\cos(u^{2})\,du$;   $S(x)=\int _{0}^{x}\sin(u^{2})\,du$.

A két ágból álló páros-spirálnak az irányítását a $t$ paraméter előjele definiálja. A koordináta-rendszer első negyedébe eső pontoknak az Origótól mért ívhossza pozitív, a harmadik negyedbe esőké negatív mértéket kap. Ugyancsak előjelezzük a pontokhoz tartozó görbületet és a görbületi sugarat: a növekvő $t$ mellett balra kanyarodó ív adott pontjában pozitív, a jobbra kanyarodónál negatív a görbület.

A kettős spirálnak az origóban inflexiós pontja van és érinti a megfelelő tengelyt. A $t\to \pm \infty$ határértékhez a görbe két aszimptotikus pontja tartozik.

Lokális adatok

A k koefficienssel adott görbén az

ívelem: $ds=k{\sqrt {\cos ^{2}t^{2}+\sin ^{2}t^{2}}}=k\,dt$,

ívhossz: $s(t)={\widehat {OP}}=k\int _{0}^{t}\,dt=k\cdot t$,

görbület: $g(t)=2k^{2}\cdot t=2ks$,

görbületi sugár: $R(t)={\frac {1}{2ks}}$,

érintő irányszöge: $\vartheta =t^{2}{\text{(rad)}}$,

a görbület és az ívhossz aránya: $g(t):s(t)=2k$.

Alkalmazása

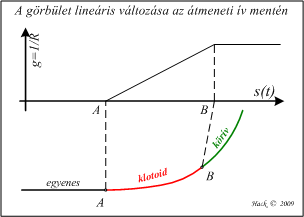
• Az utak-vasutak egyenes és köríves szakaszának összekötésére használt átmeneti ívek egyike a megfelelően választott klotoid. Alkalmazásával az egyenes és az íves szakasz között a görbület - és ezzel a járműre ható centrifugális (tehetetlenségi) erő - egyenletesen változik.

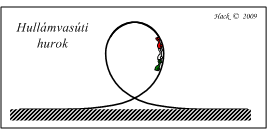
• A hullámvasutak átfordulást biztosító hurokjánál két (rendszerint szimmetrikus) klotoid ívet használnak az előzőhöz hasonló okból.

Irodalom

• Pattantyús Gépész- és Villamosmérnökök Kézikönyve 1. kötet. Műszaki Könyvkiadó, Budapest, 1961.
• Bronstein – Szemengyajev: Matematikai zsebkönyv. Műszaki könyvkiadó, Budapest, 1987. ISBN 963 1053091
• Szász Pál: A differenciál- és integrálszámítás elemei (Közoktatásügyi Kiadóvállalat, 1951)
• Pach Zs. Pálné-Frey Tamás: Vektor- és tenzoranalízis, Műszaki Könyvkiadó, Budapest,1964.