Karommentes gráf

Karom

A matematika, azon belül a gráfelmélet területén a karommentes gráf (claw-free graph) olyan gráf, mely nem tartalmazza a karomgráfot feszített részgráfként.

A karom a K_1,3 teljes páros gráf másik neve (tehát arról a csillaggráfról van szó, ami három éllel, három levéllel és egy csomóponttal rendelkezik). Egy karommentes gráf onnan ismerszik meg, hogy egyetlen feszített részgráfja sem karom; tehát semelyik négy csúcspontja között nincs ilyen módon csatlakozó három él. Ezzel egyenértékű megfogalmazás, hogy a karommentes gráf olyan gráf, melyben bármely csúcs szomszédsága egy háromszögmentes gráf komplementere.

A karommentes gráfokat eredetileg az élgráfok általánosításaként vizsgálták, de három fő felfedezést tettek velük kapcsolatban, melyek indokolták a további vizsgálódást: hogy bármely páros rendű karommentes összefüggő gráf rendelkezik teljes párosítással; a karommentes gráfok független csúcshalmazait polinom időben megtaláló algoritmusok felfedezése; a karommentes perfekt gráfok karakterizációja. Több száz matematikai tanulmány és áttekintő munka foglalkozik velük.

Példák

A szabályos ikozaéder, melynek csúcsai és élei karommentes gráfot alkotnak.

• Bármely G gráfhoz tartozó L(G) élgráf karommentes; L(G) a gráf, amiben a csúcspontok a G élei, és két csúcs akkor van összekötve, ha G-ben a két élnek volt közös végpontja. Az L(G) élgráf nem tartalmazhat karmot, mert ha a G-beli három él, e₁, e₂ és e₃ közös végponttal rendelkezik egy másik, e₄ éllel, akkor a skatulyaelv alapján az e₁, e₂ és e₃ közül valamely kettő végpontja közös kell legyen. Az élgráfok kilenc tiltott részgráf alapján jellemezhetők; ezek közül a karom a legegyszerűbb. Ez volt az a karakterizáció, ami a karommentes gráfok tanulmányozásának eredeti motivációját adta.
• A de Bruijn-gráfok (melyek csúcsai n-bites bitfüzérek, élei pedig a füzérek közötti (n − 1)-bites átfedéseket jelzik) karommentesek. Ez megmutatható úgy is, hogy az n-bites de Bruijn-gráf előállítható az (n − 1)-bites de Bruijn-gráf élgráfjaként.
• Bármely háromszögmentes gráf komplementere karommentes.
• A valódi intervallumgráfok, melyek olyan intervallumok által formált metszetgráfok, melyek közül egyik sem tartalmazza a másikat, karommentesek, mivel négy valódi mtesző intervallum nem metszheti egymást a karom mintázata szerint.
• A Moser-gráf, egy hét csúcsú gráf, ami a sík kromatikus számára ad alsó korlátot, szintén karommentes.
• Számos poliéderhez és politóphoz tartozik karommentes gráf; ilyen például a tetraéder és bármely szimplex (teljes gráf), az oktaéder és általában bármely keresztpolitóp (ami valamely teljes gráfból teljes párosítás eltávolításával kapott Turán-gráffal izomorf) a szabályok ikozaéder gráfja és a 16-cella gráfja.
• A Schläfli-gráf, ami egy 27 csúcsú erősen reguláris gráf, szintén karommentes.

Felismerésük

Egy n csúccsal és m éllel rendelkező gráf karommentessége O(n⁴) időben könnyen ellenőrizhető, a gráf minden csúcs-négyesét ellenőrizve, hogy nem alkotnak-e karmot. Ennél hatékonyabb, de bonyolultabb megoldás annak ellenőrzése a gráf minden egyes csúcsára, hogy szomszédainak komplementer gráfja nem tartalmaz-e háromszöget. Egy gráf pontosan akkor tartalmaz háromszöget, ha szomszédsági mátrixának köbének átlójában található nem nulla elem, ezért a háromszög keresése aszimptotikusan ugyanannyi idő alatt végezhető el, mint az n × n mátrixszorzás. Ezért a Coppersmith–Winograd-algoritmust használva az algoritmus futási ideje O(n^3,376).

(Kloks, Kratsch & Müller 2000) felismerése szerint bármely karommentes gráf csúcsainak legfeljebb 2√m szomszédja van, egyébként a Turán-tétel szerint a csúcsoknak nem jutna elég él ahhoz, hogy egy háromszögmentes gráf komplementerét alkossák. Ez a megfigyelés alkalmat ad arra, hogy a fent említett gyors mátrixszorzáson alapuló algoritmussal ellenőrizzük az összes szomszédságot a mátrixszorzás 2√m × 2√m idejében, vagy alacsonyabb fokszámú csúcsoknál még gyorsabban. Az algoritmus számára a legrosszabb eset, amikor Ω(√m) csúcsnak van Ω(√m) szomszédja, míg a maradéknak néhány szomszédja van, ilyenkor az összidő O(m^3,376/2) = O(m^1,688).

Leszámlálás

Mivel a karommentes gráfok háromszögmentes gráfok komplementereit tartalmazzák, az n csúcsú karommentes gráfok száma legalább olyan gyorsan nő, mint a háromszögmentes gráfoké, exponenciálisan az n négyzete arányában. Az n csúcspontú összefüggő karommentes gráfok száma n = 1, 2, ...-re:

1, 1, 2, 5, 14, 50, 191, 881, 4494, 26389, 184749, ... (A022562 sorozat az OEIS-ben).

Ha megengedjük a nem összefüggő gráfokat is, még nagyobb számokat kapunk:

1, 2, 4, 10, 26, 85, 302, 1285, 6170, ... (A086991 sorozat az OEIS-ben).

A (Palmer, Read & Robinson 2002) által vázolt technika lehetővé teszi a karommentes 3-reguláris gráfok igen hatékony leszámlálását, ami nem jellemző a gráfleszámlálási problémák esetében.

Párosítások

Sumner így bizonyítja, hogy a páros rendű karommentes összefüggő gráfok rendelkeznek teljes párosítással: ha eltávolítjuk az u-tól legmesszebb lévő egymás melletti v és w csúcsokat, összefüggő részgráf marad, amire ugyanez az eltávolítási folyamat megismételhető.

(Sumner 1974) és tőle függetlenül (Las Vergnas 1975) is bebizonyította, hogy minden páros elemszámú karommentes összefüggő gráf rendelkezik teljes párosítással. Ez azt jelenti, hogy létezik a gráfnak olyan élhalmaza, hogy a gráf minden csúcsa pontosan egy párosított él végpontja. Az eredmény élgráfokra vonatkozó speciális esetéből következik, hogy bármely gráfban, mely páros számú éllel rendelkezik, particionálható kettő hosszúságú utakra. A teljes párosítás lehetővé teszi a karommentes gráfok karakterizálását, mint pontosan azok a gráfok, melyek minden páros rendű összefüggő feszített részgráfjában van teljes párosítás.

Sumner bizonyítása ennél erősebb állítást mutat meg, miszerint bármely összefüggő karommentes gráfban található olyan szomszédos csúcspár, melyek eltávolításával a maradék gráf összefüggő marad. Ennek megmutatására Sumner veszi az egymástól lehető legtávolabb lévő u és v csúcsokat, majd úgy választja ki a w csúcsot, hogy v-nek az u-tól lehető legtávolabb lévő szomszédja legyen; megmutatja, hogy sem v, sem w nem lehet rajta a bármely más csúcstól u-ba vezető legrövidebb utak egyikén sem, így v és w eltávolításával a maradék gráf biztosan összefüggő marad. A párosított csúcsok ilyeténként történő sorozatos eltávolítása pedig az adott karommentes gráf teljes párosítását hozza létre.

Ugyanez a bizonyítási ötlet általánosabban is felhasználható: legyen u egy tetszőleges csúcs, v a tőle lehető legtávolabb lévő csúcs, w pedig v-nek az a szomszédja, ami a lehető legnagyobb távolságra van u-tól. Ekkora a v és w eltávolítása egyetlen csúcs u-tól való távolságát sem változtatja meg. Így a párosítás létrehozása az u-tól minél távolabb lévő vw párok megkeresésével és eltávolításával lineáris időben elvégezhető egy u gyökerű szélességi bejárás egyszeri posztorder bejárásával. (Chrobak, Naor & Novick 1989) megadnak egy alternatív, mélységi bejáráson alapuló lineáris algoritmust, valamint ugyanezen probléma hatékony megoldására szolgáló párhuzamos algoritmusokat.

(Faudree, Flandrin & Ryjáček 1997) számos kapcsolódó eredményt sorol fel, köztük ezeket: a páros rendű (r − 1)-szorosan összefüggő K_1,r-mentes gráfok rendelkeznek tökéletes párosítással bármely r ≥ 2-re; a legfeljebb egy 1 fokszámú csúccsal rendelkező, páratlan rendű karommentes gráfok particionálhatók egy páratlan hosszúságú körre és egy párosításra; bármely k-ra, ami legfeljebb a karommentes gráf minimális fokszámának a fele igaz, hogy ha akár k, akár a csúcsok száma (a gráf rendje) páros, akkor a gráfnak létezik k-faktora (k-reguláris feszítő részgráfja); és ha egy karommentes gráf (2k + 1)-összefüggő, akkor bármely k-élből álló párosítás teljes párosítássá egészíthető ki.

Független halmazok

Nem maximális független csúcshalmaz (a két ibolyaszínű csúcs) és egy javító út

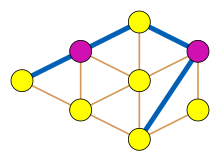
Egy élgráf független csúcshalmaza az eredeti gráf párosításának felel meg, azaz olyan élhalmaznak, melyben az élek egyike sem ered közös csúcsból. Az (Edmonds 1965) által leírt Edmonds-algoritmus bármely gráf maximális párosítását polinom időben keresi meg, ami egyenértékű az élgráf maximális független csúcshalmazának megkeresésével. Az algoritmust egymástól függetlenül (Sbihi 1980) és (Minty 1980) egészítették ki karommentes gráfokra.

Mindkét megközelítés azt használja ki, hogy a karommentes gráfokban egy csúcsnak sem lehet kettőnél több szomszédja egy független csúcshalmazban, így két független csúcshalmaz szimmetrikus differenciájának feszített részgráfjának fokszáma legalább kettő; tehát körgráfok és útgráfok uniójából előállítható. Ami főként érdekes, hogy ha I egy nem maximális független csúcshalmaz, a maximális független csúcshalmaztól csak páros körökkel és úgynevezett „javító utakkal” különbözik: ezek olyan feszített utak, melyben szereplő csúcsok váltakozva I-beliek, illetve I-n kívüliek, és végpontjaiknak csak egy szomszédjuk szerepel I-ben. Mivel I és bármelyik javító út szimmetrikus differenciája nagyobb független halmazt eredményez, a feladat redukálódott javító utak keresésére, amíg azok el nem fogynak, hasonlóan a maximális párosítást kereső algoritmushoz.

A Sbihi által leírt algoritmus az Edmonds-algoritmus virág-összehúzási lépése helyett egy hasonló, de bonyolultabb klikk-összehúzási lépést tartalmaz. Minty megközelítésében a problémagráfot transzformáljuk egy segéd-élgráffá, amin közvetlenül alkalmazzuk az Edmonds-algoritmust a javító utak megtalálására. A Nakamura & Tamura 2001 által adott javítás után Minty eredménye használható egy általánosabb probléma, a maximális súlyú független csúcshalmazok karommentes gráfokban való keresésének polinom időben történő megoldására. Ezeket az eredményeket szélesebb gráfosztályokra is sikerült általánosítani. Egy újszerű struktúratétel segítségével (Faenza, Oriolo & Stauffer 2011) megadott egy harmadfokú polinom-időben futó, súlyozott esetben is működő algoritmust.

Színezés, klikkek, domináció

Egy perfekt gráf olyan gráf, melynek kromatikus száma és klikkszáma megegyezik és ez minden feszített részgráfjára is igaz. Az erős perfektgráf-tétel alapján tudjuk, hogy a perfekt gráfok jellemezhetők úgy, mint azok a gráfok, melyek nem tartalmaznak feszített részgráfként sem páratlan kört, sem páratlan kör komplementerét (úgynevezett „páratlan lyukat”). Ez azonban évekig csak egy megoldatlan sejtés maradt, melyet csak egyes gráfosztályokra sikerült igazolni. Az ilyen gráfosztályok egyike éppen a karommentes gráfok voltak: több szerző is felfedezte, hogy a páratlan körök és páratlan lyukak nélküli karommentes gráfok perfektek. A perfekt karommentes gráfok polinom időben felismerhetők. Egy perfekt karommentes gráfban bármely csúcs szomszédsága egy páros gráf komplementerét alkotja. A perfekt karommentes gráfok polinom időben színezhetők és polinom időben találhatók bennük maximális klikkek.

A matematika megoldatlan problémája: Vajon a karommentes gráfok listakromatikus száma mindig megegyezik a kromatikus számukkal? (A matematika további megoldatlan problémái)

Általánosságban NP-nehéz probléma egy karommentes gráf legnagyobb klikkjét megtalálni. Az optimális színezése szintén NP-nehéz, mivel (az élgráfokon keresztül) a probléma a gráf élkromatikus száma kiszámításának NP-nehéz problémáját általánosítja. Hasonló okból NP-nehéz olyan színezést találni, ami 4/3-nál jobb approximációs arányt ér el. Mohó színezési algoritmussal azonban elérhető a 2 approximációs arány, mivel a karommentes gráf kromatikus száma meghaladja a maximális fokszámának felét. A lista-élszínezési sejtés szerint karommentes gráfok listakromatikus száma megegyezik a kromatikus számmal; ez a kettő más típusú gráfoknál nagyon különböző is lehet.

Bár nem minden karommentes gráf perfekt, a karommentes gráfok teljesítenek egy másik, perfekcióhoz köthető feltételt. Egy gráf akkor perfekt domináló, ha létezik olyan minimális domináló halmaza, ami független, és ez a tulajdonság minden feszített részgráfjára igaz. A karommentes gráfok ilyenek. Hogy ezt belássuk, legyen D egy karommentes gráf domináló halmaza, és tegyük fel, hogy v és w szomszédos csúcsok D-ben; ekkor a v által igen, de w által nem dominált csúcsok halmazának klikknek kell lennie (különben v lenne a karom közepe). Ha ennek a klikknek minden csúcsát már legalább egy D-beli tag dominálja, akkor v eltávolítható, ami egy kisebb független domináló halmazt eredményez, különben pedig v lecserélhető a klikk valamely nem dominált csúcsára, ami egy kevesebb szomszéddal rendelkező domináló halmazt eredményez. Ezt a cserefolyamatot ismételve végül eljutunk egy D-nél nem nagyobb domináló halmazig, így ha a kiindulási D halmaz egy minimális domináló halmaz, akkor a folyamat során egy ugyanolyan kicsi független domináló halmazhoz jutunk.

A perfekt domináló tulajdonság ellenére NP-nehéz feladat egy karommentes gráf minimális domináló halmaza méretének megállapítása. Mindazonáltal az általános gráfokhoz képest a minimális domináló halmaz vagy a minimális összefüggő domináló halmaz megkeresése rögzített paraméter mellett kezelhető (fixed-parameter tractable): a gráf mérete szerinti polinomiális szorozva a domináló halmaz mérete szerint exponenciális függvény szerinti idejű.

Struktúra

(Chudnovsky & Seymour 2005) átfogó cikksorozatukban a karommentes gráfok struktúrájának egy elméletét igazolják, a Robertson és Seymour által minorra zárt gráfosztályokra bizonyított gráfminor-tétellel, illetve a Chudnovsky, Seymour és tsai. perfekt gráfokra vonatkozó, az erős perfektgráf-tétel igazolásához használt struktúraelméletével analóg módon. Az elmélet meglehetősen bonyolult, ehelyütt két fontos eredményét emeljük ki. Az első, a karommentes gráfok egy kvázi-élgráfoknak nevezett speciális osztálya (locally co-bipartite graphs, tehát olyan gráfok, melyekben minden csúcs szomszédsága legfeljebb két klikkre particionálható), mely osztályon belül minden gráf a következő két alak valamelyikének felel meg:

1. A fuzzy circular interval graph (fuzzy körívgráf), gráfosztály, amit egy körön lévő pontok és ívek határoznak meg, ami a valódi körívgráf általánosítása.
2. Olyan gráf, ami egy multigráfból konstruálható annak minden élének fuzzy linear interval graph-ra (fuzzy lineáris intervallumgráf) való cserélésével. Ez az élgráf konstrukciójának általánosítása, ahol a multigráf minden élét egy csúcsra kell cserélni. A fuzzy lineáris intervallumgráfok pedig hasonlóak a fuzzy körívgráfokhoz, csak nem egy körön, hanem egy egyenesen jönnek létre.

Chudnovsky és Seymour bármely összefüggő karommentes gráfot a következő kategóriák egyikébe sorolnak:

1. Karommentes gráfok hat specifikus alosztálya. Ezek közül az első három élgráfok, körívgráfok és egy ikozaéder feszített részgráfjai; a másik három egyéb definíciókat tartalmaz.
2. Gráfok, melyek kisebb karommentes gráfokból hozhatók létre négy egyszerű módon.
3. Antiprizmaszerű gráfok, a sűrű gráfok egy osztálya, azok a karommentes gráfok, melyekben bármely négy csúcs közti feszített részgráf legalább két élet tartalmaz.

A struktúraelmélet jelentős része az antiprizmaszerű gráfok további analízisét célozza. Az analízis fontos részét képezi a Schläfli-gráf, tehát az srg(27,16,10,8) paraméterű karommentes erősen reguláris gráf. A struktúraelmélet a poliéder-kombinatorika területén új eredményekhez vezetett, segítségével új korlátokat állapítottak meg a karommentes gráfok kromatikus számával kapcsolatban, valamint új, rögzített paraméter mellett kezelhető algoritmusokat fedeztek fel a karommentes gráfok domináló halmazainak keresésére.

Jegyzetek

• Beineke, L. W. (1968), "Derived graphs of digraphs", in Sachs, H.; Voss, H.-J. & Walter, H.-J., Beiträge zur Graphentheorie, Leipzig: Teubner, pp. 17–33.
• Chrobak, Marek; Naor, Joseph & Novick, Mark B. (1989), "Using bounded degree spanning trees in the design of efficient algorithms on claw-free graphs", in Dehne, F.; Sack, J.-R. & Santoro, N., Algorithms and Data Structures: Workshop WADS '89, Ottawa, Canada, August 1989, Proceedings, vol. 382, Lecture Notes in Comput. Sci., Berlin: Springer, pp. 147–162, DOI 10.1007/3-540-51542-9_13.
• Chudnovsky, Maria; Robertson, Neil & Seymour, Paul et al. (2006), "The strong perfect graph theorem", Annals of Mathematics 164 (1): 51–229, doi:10.4007/annals.2006.164.51, <http://people.math.gatech.edu/~thomas/PAP/spgc.pdf>.
• Chudnovsky, Maria & Seymour, Paul (2005), "The structure of claw-free graphs", Surveys in combinatorics 2005, vol. 327, London Math. Soc. Lecture Note Ser., Cambridge: Cambridge Univ. Press, pp. 153–171.
• Cygan, Marek; Philip, Geevarghese & Pilipczuk, Marcin et al. (2011), "Dominating set is fixed parameter tractable in claw-free graphs", Theoretical Computer Science 412 (50): 6982–7000, DOI 10.1016/j.tcs.2011.09.010.
• Edmonds, Jack (1965), "Paths, Trees and Flowers", Canadian J. Math 17 (0): 449–467, DOI 10.4153/CJM-1965-045-4.
• Faenza, Yuri; Oriolo, Gianpaolo & Stauffer, Gautier (2011), "An Algorithmic Decomposition of Claw-free Graphs Leading to an O(n³)-algorithm for the Weighted Stable Set Problem", Proceedings of the Twenty-second Annual ACM-SIAM Symposium on Discrete Algorithms, SODA '11, San Francisco, California: SIAM, pp. 630–646, DOI 10.1137/1.9781611973082.49.
• Faudree, Ralph; Flandrin, Evelyne & Ryjáček, Zdeněk (1997), "Claw-free graphs — A survey", Discrete Mathematics 164 (1–3): 87–147, DOI 10.1016/S0012-365X(96)00045-3.
• Goldberg, Andrew V. & Karzanov, Alexander V. (1996), "Path problems in skew-symmetric graphs", Combinatorica 16 (3): 353–382, DOI 10.1007/BF01261321.
• Gravier, Sylvain & Maffray, Frédéric (2004), "On the choice number of claw-free perfect graphs", Discrete Mathematics 276 (1-3): 211–218, DOI 10.1016/S0012-365X(03)00292-9.
• Hermelin, Danny; Mnich, Matthias & van Leeuwen, Erik Jan et al. (2010), Domination when the stars are out.
• Itai, Alon & Rodeh, Michael (1978), "Finding a minimum circuit in a graph", SIAM Journal on Computing 7 (4): 413–423, DOI 10.1137/0207033.
• King, Andrew D. & Reed, Bruce A. (2015), "Claw-free graphs, skeletal graphs, and a stronger conjecture on ω, Δ, and χ", Journal of Graph Theory 78 (3): 157–194, DOI 10.1002/jgt.21797.
• Kloks, Ton; Kratsch, Dieter & Müller, Haiko (2000), "Finding and counting small induced subgraphs efficiently", Information Processing Letters 74 (3–4): 115–121, DOI 10.1016/S0020-0190(00)00047-8.
• Las Vergnas, M. (1975), "A note on matchings in graphs", Cahiers du Centre d'Études de Recherche Opérationnelle 17 (2-3-4): 257–260.
• Minty, George J. (1980), "On maximal independent sets of vertices in claw-free graphs", Journal of Combinatorial Theory. Series B 28 (3): 284–304, DOI 10.1016/0095-8956(80)90074-X.
• Nakamura, Daishin & Tamura, Akihisa (2001), "A revision of Minty's algorithm for finding a maximum weighted stable set of a claw-free graph", Journal of the Operations Research Society of Japan 44 (2): 194–204, <http://www.kurims.kyoto-u.ac.jp/preprint/file/RIMS1261.ps.gz>.
• Palmer, Edgar M.; Read, Ronald C. & Robinson, Robert W. (2002), "Counting claw-free cubic graphs", SIAM Journal on Discrete Mathematics 16 (1): 65–73, doi:10.1137/S0895480194274777, <http://www.cs.uga.edu/~rwr/publications/claw.pdf>.
• Sbihi, Najiba (1980), "Algorithme de recherche d'un stable de cardinalité maximum dans un graphe sans étoile", Discrete Mathematics 29 (1): 53–76, DOI 10.1016/0012-365X(90)90287-R.
• Sumner, David P. (1974), "Graphs with 1-factors", Proceedings of the American Mathematical Society (American Mathematical Society) 42 (1): 8–12, DOI 10.2307/2039666.

Fordítás

• Ez a szócikk részben vagy egészben a Claw-free graph című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

További információk

• Claw-free graphs, Information System on Graph Class Inclusions
• Mugan, Jonathan William; Weisstein, Eric W.: Claw-Free Graph (angol nyelven). Wolfram MathWorld