A koordinátageometriában a gömbi koordináták vagy térbeli polárkoordináta-rendszer egy háromdimenziós koordináta-rendszer, amiben a pontok helyét az origótól mért távolságuk és két szög adja meg.
Az origó középpontú gömbökön az origótól mért távolság konstans. Így ezeken a felületeken a pontok helyét két szöggel lehet meghatározni. Ezek a gömbi koordináták .[ 1] [ 2]
A gömbi koordináták a síkbeli polárkoordináta-rendszer egyik általánosítása. Egy másik általánosítás a hengerkoordináta-rendszer .
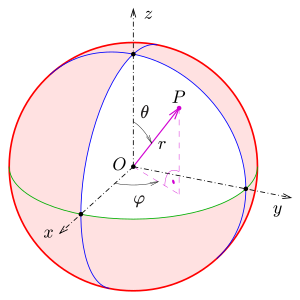
Egy
P
{\displaystyle P}
r
,
θ
,
φ
{\displaystyle r,\theta ,\varphi }
x
,
y
,
z
{\displaystyle x,y,z}
Egy gömbi koordináta-rendszert a háromdimenziós euklideszi térben a következők határoznak meg:
egy
O
{\displaystyle O}
egy, az origón áthaladó irányított egyenes (pólustengely). Ez tűzi ki a pólus irányát, és ez rögzíti az egyenlítősíkot is, ami az origóban a pólusegyenesre állított merőleges sík
egy rögzített irány az egyenlítősíkon Gyakran egy Descartes-féle koordináta-rendszert is használnak a gömbi koordináta-rendszerrel együtt. Ekkor:
annak origója a gömbi koordináta-rendszer origója
annak pólustengelye a z -tengely (így az x és y -tengelyek az egyenlítősíkban vannak
annak x -tengelye az egyenlítősíkon rögzített irány, így az y -tengely is egyértelműen meghatározott A matematikában és a fizikában általában a következő koordinátákat használják:
r
{\displaystyle r}
θ
{\displaystyle \theta }
ϑ
{\displaystyle \vartheta }
[ 3] [ 4]
0
{\displaystyle 0}
π
{\displaystyle \pi }
φ
{\displaystyle \varphi }
ϕ
{\displaystyle \phi }
[ 3] [ 4]
−
π
{\displaystyle -\pi }
π
{\displaystyle \pi }
2
π
{\displaystyle 2\pi }
Minden
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
x
=
r
⋅
sin
θ
⋅
cos
φ
y
=
r
⋅
sin
θ
⋅
sin
φ
z
=
r
⋅
cos
θ
{\displaystyle {\begin{array}{cll}x&=&r\cdot \sin \theta \cdot \cos \varphi \\y&=&r\cdot \sin \theta \cdot \sin \varphi \\z&=&r\cdot \cos \theta \end{array}}}
Ezekbe az egyenletekbe bármely
r
{\displaystyle r}
θ
{\displaystyle \theta }
φ
{\displaystyle \varphi }
r
{\displaystyle r}
θ
{\displaystyle \theta }
[
0
,
π
]
{\displaystyle [0,\pi ]}
φ
{\displaystyle \varphi }
(
−
π
,
π
]
{\displaystyle (-\pi ,\pi ]}
[
0
,
2
π
)
{\displaystyle [0,2\pi )}
z -tengely pontjai esetén
φ
{\displaystyle \varphi }
θ
{\displaystyle \theta }
φ
=
0
{\displaystyle \varphi =0}
θ
=
0
{\displaystyle \theta =0}
A többi pont esetén a fentiek szerint választott Descartes-koordináta-rendszerben adott
(
x
,
y
,
z
)
{\displaystyle (x,y,z)}
(
r
,
θ
,
φ
)
{\displaystyle (r,\theta ,\varphi )}
[ 5]
r
=
x
2
+
y
2
+
z
2
{\displaystyle {r}={\sqrt {x^{2}+y^{2}+z^{2}}}}
θ
=
arccos
z
x
2
+
y
2
+
z
2
=
arccos
z
r
=
arcctg
z
x
2
+
y
2
{\displaystyle {\theta }=\arccos {\frac {z}{\sqrt {x^{2}+y^{2}+z^{2}}}}\ =\arccos {\frac {z}{r}}\ =\ \operatorname {arcctg} {\frac {z}{\sqrt {x^{2}+y^{2}}}}}
φ
=
arctg2
(
y
,
x
)
=
{
arctg
(
y
x
)
, ha
x
>
0
,
sgn
(
y
)
π
2
, ha
x
=
0
,
arctg
(
y
x
)
+
π
, ha
x
<
0
∧
y
≥
0
,
arctg
(
y
x
)
−
π
, ha
x
<
0
∧
y
<
0.
{\displaystyle \varphi =\operatorname {arctg2} (y,x)={\begin{cases}\operatorname {arctg} \left({\frac {y}{x}}\right)&{\text{, ha }}x>0,\\\operatorname {sgn}(y){\frac {\pi }{2}}&{\text{, ha }}x=0,\\\operatorname {arctg} \left({\frac {y}{x}}\right)+\pi &{\text{, ha }}x<0\land y\geq 0,\\\operatorname {arctg} \left({\frac {y}{x}}\right)-\pi &{\text{, ha }}x<0\land y<0.\end{cases}}}
Ezek az egyenletek felteszik, hogy
φ
{\displaystyle \varphi }
−
π
{\displaystyle -\pi }
π
{\displaystyle \pi }
φ
{\displaystyle \varphi }
2
π
{\displaystyle 2\pi }
Az analízisben és alkalmazásaiban a szögkoordináták többnyire ívmértékben adják meg.
A gömbkoordinátákat gyakran használják forgásszimmetrikus rendszerek vizsgálatára. Példák: térfogatintegrálok gömbön, forgásszimmetrikus erőterek, mint például gömb alakú égitestek gravitációja, egy ponttöltés elektromos tere (lásd még: felszíni integrál). A képleteket egyszerűsíti, ha függetlenek egy vagy két gömbi koordinátától. Fontos parciális differenciálegyenletek, mint például a Laplace-egyenlet vagy a Helmholtz-egyenlet gömbi koordinátákban a változók szétválasztásával könnyen megoldhatók.
A fenti konvenció nemzetközileg használatos az elméleti fizikában. Néha a
θ
{\displaystyle \theta }
φ
{\displaystyle \varphi }
A
θ
{\displaystyle \theta }
−
90
∘
{\displaystyle -90^{\circ }}
90
∘
{\displaystyle 90^{\circ }}
ϕ
{\displaystyle \phi }
ϕ
=
90
∘
−
θ
,
θ
=
90
∘
−
ϕ
{\displaystyle \phi =90^{\circ }-\theta ,\theta =90^{\circ }-\phi }
φ
{\displaystyle \varphi }
λ
{\displaystyle \lambda }
A fenti konvenció inkonzisztens a síkbeli polárkoordináta-rendszer felépítésével. Egyes problémákhoz praktikusabb az
x
=
r
cos
ϕ
cos
φ
{\displaystyle x=r\cos \phi \,\cos \varphi }
y
=
r
cos
ϕ
sin
φ
{\displaystyle y=r\cos \phi \,\sin \varphi }
z
=
r
sin
ϕ
{\displaystyle z=r\sin \phi \quad }
ábrázolás. Ebben az ábrázolásban
ϕ
{\displaystyle \phi }
Egy
p
→
{\displaystyle {\vec {p}}}
ϕ
=
arcsin
(
z
/
r
)
{\displaystyle \phi =\arcsin(z/r)}
φ
=
atg2
(
y
,
x
)
{\displaystyle \varphi =\operatorname {atg2} (y,x)}
ahol
r
=
|
p
→
|
{\displaystyle r=|{\vec {p}}|}
Egy koordináta-transzformáció helyi tulajdonságait Jacobi-mátrixszal írják le. A gömbkoordináták transzformációját a fenti Descartes-féle koordináta-rendszerbe a következő mátrix írja le:
J
=
∂
(
x
,
y
,
z
)
∂
(
r
,
θ
,
φ
)
=
(
sin
θ
cos
φ
r
cos
θ
cos
φ
−
r
sin
θ
sin
φ
sin
θ
sin
φ
r
cos
θ
sin
φ
r
sin
θ
cos
φ
cos
θ
−
r
sin
θ
0
)
.
{\displaystyle J={\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}={\begin{pmatrix}\sin \theta \cos \varphi &r\cos \theta \cos \varphi &-r\sin \theta \sin \varphi \\\sin \theta \sin \varphi &r\cos \theta \sin \varphi &r\sin \theta \cos \varphi \\\cos \theta &-r\sin \theta &0\end{pmatrix}}.}
A hozzá tartozó funkcionáldetermináns :
det
J
=
r
2
sin
θ
{\displaystyle \det J=r^{2}\sin \theta }
A transzformáció inverzét legegyszerűbben a
J
{\displaystyle J}
J
−
1
=
∂
(
r
,
θ
,
φ
)
∂
(
x
,
y
,
z
)
=
(
sin
θ
cos
φ
sin
θ
sin
φ
cos
θ
1
r
cos
θ
cos
φ
1
r
cos
θ
sin
φ
−
1
r
sin
θ
−
1
r
sin
φ
sin
θ
1
r
cos
φ
sin
θ
0
)
.
{\displaystyle J^{-1}={\frac {\partial (r,\theta ,\varphi )}{\partial (x,y,z)}}={\begin{pmatrix}\sin \theta \cos \varphi &\sin \theta \sin \varphi &\cos \theta \\{\frac {1}{r}}\cos \theta \cos \varphi &{\frac {1}{r}}\cos \theta \sin \varphi &-{\frac {1}{r}}\sin \theta \\-{\frac {1}{r}}{\frac {\sin \varphi }{\sin \theta }}&{\frac {1}{r}}{\frac {\cos \varphi }{\sin \theta }}&0\end{pmatrix}}.}
A mátrix néhány komponense olyan tört, melynek nevezője nullává válik, ha
r
=
0
{\displaystyle \textstyle r=0}
sin
θ
=
0
{\displaystyle \textstyle \sin \theta =0}
θ
=
0
{\displaystyle \textstyle \theta =0}
π
{\displaystyle \textstyle \pi }
J
−
1
=
(
x
r
y
r
z
r
x
z
r
2
x
2
+
y
2
y
z
r
2
x
2
+
y
2
−
(
x
2
+
y
2
)
r
2
x
2
+
y
2
−
y
x
2
+
y
2
x
x
2
+
y
2
0
)
.
{\displaystyle J^{-1}={\begin{pmatrix}{\frac {x}{r}}&{\frac {y}{r}}&{\frac {z}{r}}\\\\{\frac {xz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {yz}{r^{2}{\sqrt {x^{2}+y^{2}}}}}&{\frac {-(x^{2}+y^{2})}{r^{2}{\sqrt {x^{2}+y^{2}}}}}\\\\{\frac {-y}{x^{2}+y^{2}}}&{\frac {x}{x^{2}+y^{2}}}&0\end{pmatrix}}.}
[ szerkesztés ] A Jacobi-mátrix lehetővé teszi, hogy a differenciálok átszámítását átláthatóan átírjuk lineáris leképezéssé:
(
d
x
d
y
d
z
)
=
J
⋅
(
d
r
d
θ
d
φ
)
{\displaystyle {\begin{pmatrix}\mathrm {d} x\\\mathrm {d} y\\\mathrm {d} z\end{pmatrix}}=J\cdot {\begin{pmatrix}\mathrm {d} r\\\mathrm {d} \theta \\\mathrm {d} \varphi \end{pmatrix}}}
illetve
(
d
r
d
θ
d
φ
)
=
J
−
1
⋅
(
d
x
d
y
d
z
)
{\displaystyle {\begin{pmatrix}\mathrm {d} r\\\mathrm {d} \theta \\\mathrm {d} \varphi \end{pmatrix}}=J^{-1}\cdot {\begin{pmatrix}\mathrm {d} x\\\mathrm {d} y\\\mathrm {d} z\end{pmatrix}}}
A
d
V
=
d
x
d
y
d
z
{\displaystyle \mathrm {d} V=\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z}
térfogatelem egyszerűen számítható a
det
J
=
r
2
sin
θ
{\displaystyle \det J=r^{2}\sin \theta }
funkcionáldeterminánssal, azaz:
d
V
=
r
2
sin
θ
d
φ
d
θ
d
r
{\displaystyle \,\mathrm {d} V=r^{2}\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} \theta \,\mathrm {d} r}
A
d
V
d
r
{\displaystyle {\frac {\mathrm {d} V}{\mathrm {d} r}}}
r
{\displaystyle r}
d
A
{\displaystyle \mathrm {d} A}
felszínelemet :
d
A
=
r
2
sin
θ
d
φ
d
θ
{\displaystyle \mathrm {d} A=r^{2}\sin \theta \,\mathrm {d} \varphi \,\mathrm {d} \theta }
A
d
s
{\displaystyle ds}
vonalelem számítható, mint:
d
s
2
=
d
x
2
+
d
y
2
+
d
z
2
=
d
r
2
+
r
2
d
θ
2
+
r
2
sin
2
θ
d
φ
2
{\displaystyle \mathrm {d} s^{2}=\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2}=\mathrm {d} r^{2}+r^{2}\mathrm {d} \theta ^{2}+r^{2}\sin ^{2}\theta \mathrm {d} \varphi ^{2}}
A
d
s
{\displaystyle ds}
metrikus tenzornak sincsenek koordinátái a főátlón kívül:
g
=
J
T
J
=
(
1
0
0
0
r
2
0
0
0
r
2
sin
2
θ
)
{\displaystyle g=J^{T}J={\begin{pmatrix}1&0&0\\0&r^{2}&0\\0&0&r^{2}\sin ^{2}\theta \end{pmatrix}}}
A metrikus tenzor nyilván a
h
=
diag
(
1
,
r
,
r
sin
θ
)
{\displaystyle h=\operatorname {diag} (1,r,r\sin \theta )}
diagonális mátrix négyzete. Ennek segítségével a Jacobi-mátrix írható úgy, mint
J
=
S
h
{\displaystyle J=Sh}
S
{\displaystyle S}
S
=
(
sin
θ
cos
φ
cos
θ
cos
φ
−
sin
φ
sin
θ
sin
φ
cos
θ
sin
φ
cos
φ
cos
θ
−
sin
θ
0
)
{\displaystyle S={\begin{pmatrix}\sin \theta \cos \varphi &\cos \theta \cos \varphi &-\sin \varphi \\\sin \theta \sin \varphi &\cos \theta \sin \varphi &\cos \varphi \\\cos \theta &-\sin \theta &0\end{pmatrix}}}
forgatómátrix .
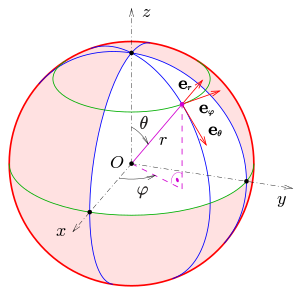
Egy pont gömbi koordinátái a helyfüggő
e
r
,
e
θ
,
e
φ
{\displaystyle \mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi }}
A következőkben vektorok és operátorok transzformációit mutatjuk be. Az eredmények leírásánál előnyben részesítjük a kompakt mátrixos formát. A legtöbb kijelentés és képlet a
z
{\displaystyle z}
A
φ
{\displaystyle \varphi }
e
φ
{\displaystyle \mathbf {e} _{\varphi }}
bázisvektor adja meg egy
P
(
r
,
θ
,
φ
)
{\displaystyle P(r,\theta ,\varphi )}
φ
{\displaystyle \varphi }
d
φ
{\displaystyle d\varphi }
infinitezimális mennyiséggel elmozdítjuk:
e
φ
∼
∂
P
∂
φ
{\displaystyle \mathbf {e} _{\varphi }\sim {\frac {\partial \mathrm {P} }{\partial \varphi }}}
Ebből
e
φ
∼
∂
P
∂
φ
=
∂
x
∂
φ
e
x
+
∂
y
∂
φ
e
y
+
∂
z
∂
φ
e
z
=
−
r
sin
θ
sin
φ
e
x
+
r
sin
θ
cos
φ
e
y
{\displaystyle \mathbf {e} _{\varphi }\sim {\frac {\partial \mathrm {P} }{\partial \varphi }}={\frac {\partial x}{\partial \varphi }}\mathbf {e} _{x}+{\frac {\partial y}{\partial \varphi }}\mathbf {e} _{y}+{\frac {\partial z}{\partial \varphi }}\mathbf {e} _{z}=-r\sin \theta \sin \varphi \mathbf {e} _{x}+r\sin \theta \cos \varphi \mathbf {e} _{y}}
Ahhoz, hogy ortonormált bázist kapjunk, még le kell normálni az
e
φ
{\displaystyle e_{\varphi }}
e
φ
=
−
sin
φ
e
x
+
cos
φ
e
y
{\displaystyle \mathbf {e} _{\varphi }=-\sin \varphi \,\mathbf {e} _{x}+\cos \varphi \,\mathbf {e} _{y}}
Hasonlóan kapjuk az
e
r
{\displaystyle e_{r}}
e
θ
{\displaystyle e_{\theta }}
e
r
=
sin
θ
cos
φ
e
x
+
sin
θ
sin
φ
e
y
+
cos
θ
e
z
{\displaystyle \mathbf {e} _{r}=\sin \theta \cos \varphi \,\mathbf {e} _{x}+\sin \theta \sin \varphi \,\mathbf {e} _{y}+\cos \theta \,\mathbf {e} _{z}}
e
θ
=
cos
θ
cos
φ
e
x
+
cos
θ
sin
φ
e
y
−
sin
θ
e
z
{\displaystyle \mathbf {e} _{\theta }=\cos \theta \cos \varphi \,\mathbf {e} _{x}+\cos \theta \sin \varphi \,\mathbf {e} _{y}-\sin \theta \,\mathbf {e} _{z}}
Oszlopvektorba írva:
e
r
=
(
sin
θ
cos
φ
sin
θ
sin
φ
cos
θ
)
,
e
θ
=
(
cos
θ
cos
φ
cos
θ
sin
φ
−
sin
θ
)
,
e
φ
=
(
−
sin
φ
cos
φ
0
)
{\displaystyle \mathbf {e} _{r}={\begin{pmatrix}\sin \theta \cos \varphi \\\sin \theta \sin \varphi \\\cos \theta \end{pmatrix}},\qquad \mathbf {e} _{\theta }={\begin{pmatrix}\cos \theta \cos \varphi \\\cos \theta \sin \varphi \\-\sin \theta \end{pmatrix}},\qquad \mathbf {e} _{\varphi }={\begin{pmatrix}-\sin \varphi \\\cos \varphi \\0\end{pmatrix}}}
Ezek a bázisvektorok az
e
r
,
e
θ
,
e
φ
{\displaystyle \mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi }}
A fent bevezetett
S
{\displaystyle S}
(
e
r
,
e
θ
,
e
φ
)
=
(
e
x
,
e
y
,
e
z
)
⋅
S
{\displaystyle (\mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi })=(\mathbf {e} _{x},\mathbf {e} _{y},\mathbf {e} _{z})\cdot S}
Mivel
S
{\displaystyle S}
(
e
x
,
e
y
,
e
z
)
=
(
e
r
,
e
θ
,
e
φ
)
⋅
S
T
{\displaystyle (\mathbf {e} _{x},\mathbf {e} _{y},\mathbf {e} _{z})=(\mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi })\cdot S^{T}}
Az egyes koordinátákhoz tartozó irányokat nevezik radiális, meridionális és azimutális irányoknak. Ezek a fogalmak nemcsak a csillagászatban és a földtudományokban, hanem a fizikában, a matematikában és mérnöki tudományokban is fontosak. Például a Hertz-dipólus esetén, ha az antenna kifeszítésének iránya a
z
{\displaystyle z}
Egy vektornak, mint geometriai entitásnak, függetlennek kell lennie a koordináta-rendszertől:
A
x
e
x
+
A
y
e
y
+
A
z
e
z
=
A
=
A
r
e
r
+
A
θ
e
θ
+
A
φ
e
φ
.
{\displaystyle A_{x}\mathbf {e} _{x}+A_{y}\mathbf {e} _{y}+A_{z}\mathbf {e} _{z}=\mathbf {A} =A_{r}\mathbf {e} _{r}+A_{\theta }\mathbf {e} _{\theta }+A_{\varphi }\mathbf {e} _{\varphi }.}
Ez úgy teljesül, hogy:
(
A
x
A
y
A
z
)
=
S
⋅
(
A
r
A
θ
A
φ
)
{\displaystyle {\begin{pmatrix}A_{x}\\A_{y}\\A_{z}\end{pmatrix}}=S\cdot {\begin{pmatrix}A_{r}\\A_{\theta }\\A_{\varphi }\end{pmatrix}}}
(
A
r
A
θ
A
φ
)
=
S
T
⋅
(
A
x
A
y
A
z
)
{\displaystyle {\begin{pmatrix}A_{r}\\A_{\theta }\\A_{\varphi }\end{pmatrix}}=S^{T}\cdot {\begin{pmatrix}A_{x}\\A_{y}\\A_{z}\end{pmatrix}}}
A parciális deriváltak szintén transzformálódnak, de normálás nélkül. A fentiekhez hasonlóan számolhatunk, de most kihagyjuk a
P
{\displaystyle P}
J
=
S
h
{\displaystyle J=Sh}
S
{\displaystyle S}
(
∂
∂
r
,
∂
∂
θ
,
∂
∂
φ
)
=
(
∂
∂
x
,
∂
∂
y
,
∂
∂
z
)
⋅
J
{\displaystyle \left({\frac {\partial }{\partial r}},{\frac {\partial }{\partial \theta }},{\frac {\partial }{\partial \varphi }}\right)=\left({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right)\cdot J}
és az inverz transzformáció:
(
∂
∂
x
,
∂
∂
y
,
∂
∂
z
)
=
(
∂
∂
r
,
∂
∂
θ
,
∂
∂
φ
)
⋅
J
−
1
{\displaystyle \left({\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right)=\left({\frac {\partial }{\partial r}},{\frac {\partial }{\partial \theta }},{\frac {\partial }{\partial \varphi }}\right)\cdot J^{-1}}
A
∇
{\displaystyle \nabla }
∇
=
e
x
∂
∂
x
+
e
y
∂
∂
y
+
e
z
∂
∂
z
{\displaystyle \mathbf {\nabla } =\mathbf {e} _{x}{\frac {\partial }{\partial x}}+\mathbf {e} _{y}{\frac {\partial }{\partial y}}+\mathbf {e} _{z}{\frac {\partial }{\partial z}}}
A fent levezetett módon transzformálva az egységvektorokat és a parciális deriváltakat:
∇
=
e
r
∂
∂
r
+
e
θ
1
r
∂
∂
θ
+
e
φ
1
r
sin
θ
∂
∂
φ
{\displaystyle \mathbf {\nabla } =\mathbf {e} _{r}{\frac {\partial }{\partial r}}+\mathbf {e} _{\theta }{\frac {1}{r}}{\frac {\partial }{\partial \theta }}+\mathbf {e} _{\varphi }{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \varphi }}}
Ebben a formában alkalmazható a transzformált nabla-operátor egy gömbkoordinátákkal adott skalármező gradiensének számítására.
Egy gömbi koordinátákkal adott A vektormező divergenciájának kiszámításához tekintetbe kell venni, hogy a
∇
{\displaystyle \nabla }
A
r
,
A
θ
,
A
φ
{\displaystyle A_{r},A_{\theta },A_{\varphi }}
A -ban implicit jelenlevő
e
r
,
e
θ
,
e
φ
{\displaystyle \mathbf {e} _{r},\mathbf {e} _{\theta },\mathbf {e} _{\varphi }}
∇
⋅
A
=
1
r
2
∂
∂
r
(
r
2
A
r
)
+
1
r
sin
θ
∂
∂
θ
(
sin
θ
A
θ
)
+
1
r
sin
θ
∂
∂
φ
A
φ
.
{\displaystyle \mathbf {\nabla } \cdot \mathbf {A} ={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}(r^{2}A_{r})+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \theta }}(\sin \theta A_{\theta })+{\frac {1}{r\sin \theta }}{\frac {\partial }{\partial \varphi }}A_{\varphi }.}
Ugyanerre a rotáció számításánál is ügyelni kell:
∇
×
A
=
1
r
sin
θ
(
∂
∂
θ
(
A
φ
sin
θ
)
−
∂
A
θ
∂
φ
)
e
r
+
1
r
(
1
sin
θ
∂
A
r
∂
φ
−
∂
∂
r
(
r
A
φ
)
)
e
θ
+
1
r
(
∂
∂
r
(
r
A
θ
)
−
∂
A
r
∂
θ
)
e
φ
{\displaystyle \mathbf {\nabla } \times \mathbf {A} ={1 \over r\sin \theta }\left({\partial \over \partial \theta }(A_{\varphi }\sin \theta )-{\partial A_{\theta } \over \partial \varphi }\right)\mathbf {e} _{r}+{1 \over r}\left({1 \over \sin \theta }{\partial A_{r} \over \partial \varphi }-{\partial \over \partial r}(rA_{\varphi })\right)\mathbf {e} _{\theta }+{1 \over r}\left({\partial \over \partial r}(rA_{\theta })-{\partial A_{r} \over \partial \theta }\right)\mathbf {e} _{\varphi }}
Ha az A vektormező divergenciaoperátorát behelyettesítjük a
∇
{\displaystyle \nabla }
Δ
=
∇
2
=
1
r
2
∂
∂
r
(
r
2
∂
∂
r
)
+
1
r
2
sin
θ
∂
∂
θ
(
sin
θ
∂
∂
θ
)
+
1
r
2
sin
2
θ
∂
2
∂
φ
2
{\displaystyle \mathbf {\Delta } =\mathbf {\nabla } ^{2}={\frac {1}{r^{2}}}{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial }{\partial r}}\right)+{\frac {1}{r^{2}\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}}
illetve
Δ
=
∂
2
∂
r
2
+
2
r
∂
∂
r
+
1
r
2
∂
2
∂
θ
2
+
1
r
2
cos
θ
sin
θ
∂
∂
θ
+
1
r
2
sin
2
θ
∂
2
∂
φ
2
{\displaystyle \mathbf {\Delta } ={\frac {\partial ^{2}}{\partial r^{2}}}+{\frac {2}{r}}{\frac {\partial }{\partial r}}+{\frac {1}{r^{2}}}{\frac {\partial ^{2}}{\partial \theta ^{2}}}+{\frac {1}{r^{2}}}{\frac {\cos \theta }{\sin \theta }}{\frac {\partial }{\partial \theta }}+{\frac {1}{r^{2}\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}}
A gömbi koordináták egy általánosítása
n
{\displaystyle n}
x
1
=
r
cos
(
ϕ
1
)
x
2
=
r
sin
(
ϕ
1
)
cos
(
ϕ
2
)
x
3
=
r
sin
(
ϕ
1
)
sin
(
ϕ
2
)
cos
(
ϕ
3
)
⋮
x
n
−
1
=
r
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
cos
(
ϕ
n
−
1
)
x
n
=
r
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
sin
(
ϕ
n
−
1
)
{\displaystyle {\begin{aligned}x_{1}&=r\cos(\phi _{1})\\x_{2}&=r\sin(\phi _{1})\cos(\phi _{2})\\x_{3}&=r\sin(\phi _{1})\sin(\phi _{2})\cos(\phi _{3})\\&{}\,\,\,\vdots \\x_{n-1}&=r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})\\x_{n}&=r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})\end{aligned}}}
Belátható, hogy ez az
n
=
2
{\displaystyle n=2}
n
=
3
{\displaystyle n=3}
[ 6]
A szögek számítása:
tg
(
ϕ
n
−
1
)
=
x
n
x
n
−
1
tg
(
ϕ
n
−
2
)
=
x
n
2
+
x
n
−
1
2
x
n
−
2
⋮
tg
(
ϕ
1
)
=
x
n
2
+
x
n
−
1
2
+
⋯
+
x
2
2
x
1
{\displaystyle {\begin{aligned}\operatorname {tg} (\phi _{n-1})&={\frac {x_{n}}{x_{n-1}}}\\\operatorname {tg} (\phi _{n-2})&={\frac {\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}}}{x_{n-2}}}\\&{}\,\,\,\vdots \\\operatorname {tg} (\phi _{1})&={\frac {\sqrt {{x_{n}}^{2}+{x_{n-1}}^{2}+\cdots +{x_{2}}^{2}}}{x_{1}}}\end{aligned}}}
Átszámozással rekurziós képletet kapunk a szögekre:
x
n
=
r
cos
(
ϕ
n
−
1
)
x
n
−
1
=
r
sin
(
ϕ
n
−
1
)
cos
(
ϕ
n
−
2
)
x
n
−
2
=
r
sin
(
ϕ
n
−
1
)
sin
(
ϕ
n
−
2
)
cos
(
ϕ
n
−
3
)
⋮
x
2
=
r
sin
(
ϕ
n
−
1
)
⋯
sin
(
ϕ
2
)
cos
(
ϕ
1
)
x
1
=
r
sin
(
ϕ
n
−
1
)
⋯
sin
(
ϕ
2
)
sin
(
ϕ
1
)
{\displaystyle {\begin{aligned}x_{n}&=r\cos(\phi _{n-1})\\x_{n-1}&=r\sin(\phi _{n-1})\cos(\phi _{n-2})\\x_{n-2}&=r\sin(\phi _{n-1})\sin(\phi _{n-2})\cos(\phi _{n-3})\\&{}\,\,\,\vdots \\x_{2}&=r\sin(\phi _{n-1})\cdots \sin(\phi _{2})\cos(\phi _{1})\\x_{1}&=r\sin(\phi _{n-1})\cdots \sin(\phi _{2})\sin(\phi _{1})\end{aligned}}}
Ahonnan adódnak a következő szögek:
‖
L
→
k
‖
=
sgn
(
x
k
)
x
k
2
+
‖
L
→
k
−
1
‖
2
=
x
k
‖
x
k
‖
x
k
2
+
‖
L
→
k
−
1
‖
2
{\displaystyle \left\Vert {\vec {L}}_{k}\right\Vert =\operatorname {sgn}(x_{k}){\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}={\frac {x_{k}}{\left\Vert x_{k}\right\Vert }}{\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}}
ahol
‖
L
→
0
‖
=
0
{\displaystyle \left\Vert {\vec {L}}_{0}\right\Vert =0}
tg
(
ϕ
k
)
=
x
k
2
+
‖
L
→
k
−
1
‖
2
x
k
+
1
=
‖
L
→
k
‖
x
k
+
1
{\displaystyle \operatorname {tg} (\phi _{k})={\frac {\sqrt {x_{k}^{2}+\left\Vert {\vec {L}}_{k-1}\right\Vert ^{2}}}{x_{k+1}}}={\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}}
A sugár:
r
=
‖
L
→
n
‖
{\displaystyle r=\left\Vert {\vec {L}}_{n}\right\Vert }
Az árkusz tangens miatt esetszétválasztás adódik a megfelelő Descartes-koordinátával bezárt szögre, ahol is a képleteket kiterjesztjük az
arctan
(
±
∞
)
=
±
π
2
{\displaystyle \arctan(\pm \,\infty )=\pm \,{\tfrac {\pi }{2}}}
ϕ
k
=
{
arctg
(
‖
L
→
k
‖
x
k
+
1
)
+
π
,
(1) ha:
x
k
+
1
<
0
∧
k
=
n
−
1
arctg
(
‖
L
→
k
‖
x
k
+
1
)
,
(2) ha:
nem (1)
∧
nem (3)
0
,
(3) ha:
x
k
+
1
=
‖
L
→
k
‖
=
0
{\displaystyle {\begin{aligned}\phi _{k}={\begin{cases}\operatorname {arctg} \left({\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}\right)+\pi ,&{\text{(1) ha: }}x_{k+1}<0\;\land \;k=n-1\\\operatorname {arctg} \left({\frac {\left\Vert {\vec {L}}_{k}\right\Vert }{x_{k+1}}}\right),&{\text{(2) ha: }}{\text{nem (1)}}\land \;{\text{nem (3)}}\\0,&{\text{(3) ha: }}x_{k+1}=\left\Vert {\vec {L}}_{k}\right\Vert =0\\\end{cases}}\end{aligned}}}
Innen látszik, hogy
L
→
k
{\displaystyle {\begin{aligned}{\vec {L}}_{k}\end{aligned}}}
k
>
0
{\displaystyle {\begin{aligned}k>0\end{aligned}}}
A gömbkoordináták Jacobi-mátrixa a fenti számozás szerint:
J
=
(
cos
(
ϕ
1
)
−
r
sin
(
ϕ
1
)
0
0
⋯
0
sin
(
ϕ
1
)
cos
(
ϕ
2
)
r
cos
(
ϕ
1
)
cos
(
ϕ
2
)
−
r
sin
(
ϕ
1
)
sin
(
ϕ
2
)
0
⋯
0
⋮
⋮
⋱
⋱
⋱
⋮
⋮
⋮
⋱
⋱
⋱
0
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
cos
(
ϕ
n
−
1
)
r
cos
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
cos
(
ϕ
n
−
1
)
⋯
⋯
⋯
−
r
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
sin
(
ϕ
n
−
1
)
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
sin
(
ϕ
n
−
1
)
r
cos
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
sin
(
ϕ
n
−
1
)
⋯
⋯
⋯
r
sin
(
ϕ
1
)
⋯
sin
(
ϕ
n
−
2
)
cos
(
ϕ
n
−
1
)
)
{\displaystyle J=\left({\begin{matrix}\cos(\phi _{1})&-r\sin(\phi _{1})&0&0&\cdots &0\\\sin(\phi _{1})\cos(\phi _{2})&r\cos(\phi _{1})\cos(\phi _{2})&-r\sin(\phi _{1})\sin(\phi _{2})&0&\cdots &0\\\vdots &\vdots &\ddots &\ddots &\ddots &\vdots \\\vdots &\vdots &\ddots &\ddots &\ddots &0\\\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})&r\cos(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})&\cdots &\cdots &\cdots &-r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})\\\sin(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})&r\cos(\phi _{1})\cdots \sin(\phi _{n-2})\sin(\phi _{n-1})&\cdots &\cdots &\cdots &r\sin(\phi _{1})\cdots \sin(\phi _{n-2})\cos(\phi _{n-1})\end{matrix}}\right)}
Determinánsa:
det
J
(
n
)
=
r
n
−
1
sin
(
ϕ
1
)
n
−
2
sin
(
ϕ
2
)
n
−
3
⋯
sin
(
ϕ
n
−
2
)
=
r
n
−
1
⋅
∏
k
=
2
n
−
1
(
sin
(
ϕ
n
−
k
)
)
k
−
1
n
≥
2
{\displaystyle \det J_{(n)}=r^{n-1}\sin(\phi _{1})^{n-2}\sin(\phi _{2})^{n-3}\cdots \sin(\phi _{n-2})=\displaystyle r^{n-1}\cdot \prod _{k=2}^{n-1}\left(\sin(\phi _{n-k})\right)^{k-1}\quad n\geq 2}
A determináns normája fölötti integrál kifejezhető a
Γ
{\displaystyle \Gamma }
∫
0
R
∫
0
2
π
∫
0
π
…
∫
0
π
|
det
J
(
n
)
|
d
ϕ
1
…
d
ϕ
n
−
2
d
ϕ
n
−
1
d
r
=
2
π
R
n
n
⋅
∏
k
=
2
n
−
1
∫
0
π
(
sin
(
ϕ
n
−
k
)
)
k
−
1
d
ϕ
n
−
k
=
2
π
R
n
n
⋅
∏
k
=
2
n
−
1
π
Γ
(
k
2
)
Γ
(
k
+
1
2
)
=
π
n
R
n
Γ
(
n
2
+
1
)
n
≥
2
{\displaystyle \int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }\dots \int _{0}^{\pi }|\det J_{(n)}|\,{\text{d}}\phi _{1}\dots {\text{d}}\phi _{n-2}{\text{d}}\phi _{n-1}{\text{d}}r={\frac {2\pi R^{n}}{n}}\cdot \prod _{k=2}^{n-1}\int _{0}^{\pi }(\sin(\phi _{n-k}))^{k-1}{\text{d}}\phi _{n-k}={\frac {2\pi R^{n}}{n}}\cdot \prod _{k=2}^{n-1}{\frac {{\sqrt {\pi }}\;\Gamma \left({\frac {k}{2}}\right)}{\Gamma \left({\frac {k+1}{2}}\right)}}={\frac {{\sqrt {\pi }}^{n}R^{n}}{\Gamma \left({\frac {n}{2}}+1\right)}}\quad n\geq 2}
ami megfelel az
n
{\displaystyle n}
hipergömb térfogatának:
V
n
(
R
)
=
π
n
R
n
Γ
(
n
2
+
1
)
{\displaystyle V_{n}(R)={\frac {{\sqrt {\pi }}^{n}R^{n}}{\Gamma \left({\frac {n}{2}}+1\right)}}}
2D:
∫
0
R
∫
0
2
π
r
d
ϕ
1
d
r
=
π
R
2
{\displaystyle \int _{0}^{R}\int _{0}^{2\pi }r\mathrm {d} \phi _{1}\mathrm {d} r=\pi R^{2}}
3D:
∫
0
R
∫
0
2
π
∫
0
π
r
2
sin
(
ϕ
2
)
d
ϕ
2
d
ϕ
1
d
r
=
4
π
R
3
3
{\displaystyle \int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }r^{2}\sin(\phi _{2}){\text{d}}\phi _{2}{\text{d}}\phi _{1}{\text{d}}r={\frac {4\pi R^{3}}{3}}}
4D:
∫
0
R
∫
0
2
π
∫
0
π
∫
0
π
r
3
sin
2
(
ϕ
1
)
sin
(
ϕ
2
)
d
ϕ
1
d
ϕ
2
d
ϕ
3
d
r
=
π
2
R
4
2
{\displaystyle \int _{0}^{R}\int _{0}^{2\pi }\int _{0}^{\pi }\int _{0}^{\pi }r^{3}\sin ^{2}(\phi _{1})\sin(\phi _{2}){\text{d}}\phi _{1}{\text{d}}\phi _{2}{\text{d}}\phi _{3}{\text{d}}r={\frac {\pi ^{2}R^{4}}{2}}}
Az
n
=
3
{\displaystyle n=3}
x
,
y
,
z
{\displaystyle x,y,z}
x
3
=
z
=
r
cos
(
ϕ
2
)
x
2
=
x
=
r
sin
(
ϕ
2
)
cos
(
ϕ
1
)
x
1
=
y
=
r
sin
(
ϕ
2
)
sin
(
ϕ
1
)
{\displaystyle {\begin{aligned}x_{3}&=z=r\cos(\phi _{2})\\x_{2}&=x=r\sin(\phi _{2})\cos(\phi _{1})\\x_{1}&=y=r\sin(\phi _{2})\sin(\phi _{1})\\\end{aligned}}}
Ekkor a szögek:
tg
(
ϕ
2
)
=
‖
L
→
2
‖
x
3
=
x
2
2
+
x
1
2
x
3
=
x
2
+
y
2
z
tg
(
ϕ
1
)
=
‖
L
→
1
‖
x
2
=
x
1
2
x
2
=
y
x
{\displaystyle {\begin{aligned}\operatorname {tg} (\phi _{2})={\frac {\left\Vert {\vec {L}}_{2}\right\Vert }{x_{3}}}&={\frac {\sqrt {x_{2}^{2}+x_{1}^{2}}}{x_{3}}}={\frac {\sqrt {x^{2}+y^{2}}}{z}}\\\operatorname {tg} (\phi _{1})={\frac {\left\Vert {\vec {L}}_{1}\right\Vert }{x_{2}}}&={\frac {\sqrt {x_{1}^{2}}}{x_{2}}}={\frac {y}{x}}\end{aligned}}}
A gömbi koordináták transzformációjának Descartes-koordináta-rendszerbe:[ 6]
det
∂
(
x
1
,
…
,
x
n
)
∂
(
r
,
ϑ
1
,
…
,
ϑ
n
−
2
,
φ
)
=
r
n
−
1
sin
ϑ
1
(
sin
ϑ
2
)
2
⋯
(
sin
ϑ
n
−
2
)
n
−
2
{\displaystyle \det {\frac {\partial (x_{1},\dotsc ,x_{n})}{\partial (r,\vartheta _{1},\dotsc ,\vartheta _{n-2},\varphi )}}=r^{n-1}\sin \vartheta _{1}\left(\sin \vartheta _{2}\right)^{2}\dotsm \left(\sin \vartheta _{n-2}\right)^{n-2}}
Ezzel az
n
{\displaystyle n}
d
V
=
r
n
−
1
sin
ϑ
1
(
sin
ϑ
2
)
2
⋯
(
sin
ϑ
n
−
2
)
n
−
2
d
r
d
φ
d
ϑ
1
⋯
d
ϑ
n
−
2
=
r
n
−
1
d
r
d
φ
∏
j
=
1
n
−
2
(
sin
ϑ
j
)
j
d
ϑ
j
.
{\displaystyle {\begin{matrix}\mathrm {d} V&=&r^{n-1}\sin \vartheta _{1}\left(\sin \vartheta _{2}\right)^{2}\dotsm \left(\sin \vartheta _{n-2}\right)^{n-2}\mathrm {d} r\ \mathrm {d} \varphi \ \mathrm {d} \vartheta _{1}\dotsm \mathrm {d} \vartheta _{n-2}\\&=&r^{n-1}\ \mathrm {d} r\ \mathrm {d} \varphi \ \prod \limits _{j=1}^{n-2}(\sin \vartheta _{j})^{j}\ \mathrm {d} \vartheta _{j}\end{matrix}}.}
↑ Richard Doerfling: Mathematik für Ingenieure und Techniker. Oldenbourg Verlag, Seite 169.
↑ F. W. Schäfke: Einführung in die Theorie der speziellen Funktionen der mathematischen Physik. Springer, 1963, ISBN 978-3-642-94867-1 , Seite 129.
↑ a b Lothar Papula : Mathematik für Ingenieure und Naturwissenschaftler. Band 3: Vektoranalysis, Wahrscheinlichkeitsrechnung, mathematische Statistik, Fehler- und Ausgleichsrechnung. 4. verbesserte Auflage. Vieweg + Teubner, Wiesbaden 2001, ISBN 3-528-34937-9 .↑ a b Archiválva dátummal a(z) www-m8.ma.tum.de archívumban . (PDF; 59 kB). Skript an der TU München. ↑ Kugelkoordinaten. ↑ a b Herbert Amann, Joachim Escher: Analysis III. Birkhäuser 2008, ISBN 978-3-7643-8883-6 , S. 205 (eingeschränkte Online-Kopie a Google Könyvekben -USA ).
Ez a szócikk részben vagy egészben a Kugelkoordinaten
















![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)































































































