Gömbi koordináták
A gömbfelület pontjait a felületi koordináta-rendszerekben adhatjuk meg. A koordináták mérőszáma a kör alakú koordinátavonalak ívének középponti szöge. Az elméleti vizsgálatokra használt rendszerekben ezeket a szögeket ívmértékben (radián) mérjük. Az R sugarú gömb centrumát derékszögű rendszer origójába helyezve adjuk meg a felületi pontok térbeli helyzetét.
(Az ún. „gömbkoordináták” térbeli, 3D-os polárkoordináták)
Geodetikus koordináták
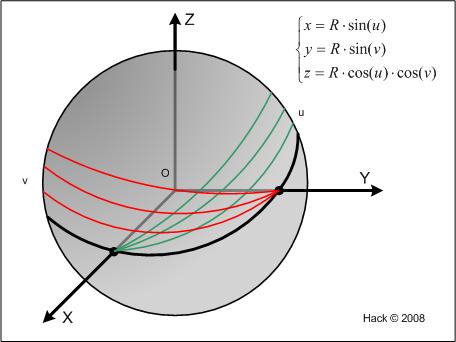
[szerkesztés]Az [u;v] koordináta-rendszer konstans vonalait a térbeli koordináta-rendszer Ox és Oy tengelyeire illeszkedő síkok metszik ki a gömbfelületből: geodetikus vonalak. Kézenfekvő a két térbeli tengely pozitív felének a felületi pontját "pólusnak" választani és a két pólust összekötő főkörön fekvő közös vonalat választani kezdetnek. Ennek a főkörnek a pontjai nem adhatók meg egyértelműen: minden pontja [0;0]. A koordináták értékkészlete: u,v := [-π;+π]
Polárkoordináták
[szerkesztés]A [λ;β] koordináta-rendszer konstans vonalait a Descartes koordináta-rendszer Oz tengelyére illeszkedő illetve a rá merőleges síkok metszik ki a gömbfelületből. A pólus = (0; 0; R)= [?;0]. A λ felületi koordináta határozatlan.
A koordináták értékkészlete: λ:= [0;2π]; β:= [0;π].
Ekvatoriális koordináták
[szerkesztés](Lásd még: földrajzi koordináták és csillagászati koordináta-rendszer)
A [λ;φ] koordináta-rendszer a polárkoordinátáktól csak a második koordináta skálázásában különbözik.
A koordináták elnevezése: hosszúság (λ); szélesség (φ). Értékkészletük: λ:= [0;2π]; φ:= [-π/2;+π/2].
A két pólus: (0; 0; ± R)=[?;± π/2]. A λ felületi koordináta határozatlan. A φ=0 szélesség-vonal az egyenlítő (equator). A konstans szélességi vonalak a szélességi körök (paralellák). A konstans hosszúsági vonalak a hosszúsági körök (meridiánok, délkörök).
Források
[szerkesztés]- Pattantyús Á. Géza. Matematikai képletek, táblázatok. Budapest: Műszaki Könyvkiadó (1961)
- Bartsch, Hans-Jochen. Matematische Formeln. Leipzig: VEB Fachbuchverlag. ASIN B0000BG4MY (1967)