Bessel-függvény
A matematikában a Bessel-függvények a Bessel-féle differenciálegyenlet kanonikus megoldásai (y(x)). A Bessel-féle differenciálegyenlet:
Ezt a függvényt először Daniel Bernoulli (1700 – 1782) svájci fizikus definiálta, majd Friedrich Bessel (1784 – 1846) német matematikus általánosította, és róla nevezték el a függvényeket.
A differenciálegyenlet igaz bármely valós vagy komplex α-ra (ez a függvény rendszáma). A legfontosabb esetekben α egy egész vagy félegész szám. A differenciálegyenletnek két fajta megoldása ismeretes: ezek az I. fajú Bessel-függvény (Jα) és a II. fajú Bessel-függvény (Yα) (Neumann-függvény). Létezik egy III. fajú függvény is, de ezt inkább Hankel-függvénynek hívják, mely a I. fajú Bessel-függvény és a II. fajú Bessel függvény speciális kombinációja.
Alkalmazások
[szerkesztés]A Bessel-függvények a Laplace-egyenlet és a Helmholtz-egyenletek megoldásaira használják hengerkoordináta-rendszerben, vagy gömbi koordináták rendszerében. A Bessel-függvények különösen fontosak a hullámterjedési problémák megoldásánál, és statikuspotenciál-problémák esetén. Hengerkoordináta-rendszerben a Bessel-függvényeknél az α=n; gömbi koordináták rendszerében a félegész szám rendű megoldás alkalmazható (α = n+1/2).
Példák az alkalmazási területekre
[szerkesztés]- Elektromágneses hullámok (elektromágneses sugárzás) megoldása hengerkoordináta-rendszerben,
- Hővezetés hengerkoordináta-rendszerben,
- Vékony akusztikus membránok rezgéseinek elemzése
- Diffúziós problémák rácsszerkezetekben
- A radiális Schrödinger-egyenlet megoldásai szabad részecskékre
- Akusztikus sugárzás megoldásai
- Jelfeldolgozásban: FM szintézis, Kaiser-ablak, Bessel-szűrő
I. fajú Bessel-függvény (Jα)
[szerkesztés]
II. fajú Bessel-függvény (Yα)
[szerkesztés]
Bessel-integrál
[szerkesztés]n egész értékekre a Bessel-függvény definiálható integrállal is:
Egy másik analóg kifejezés integrállal:
Bessel ezt a kifejezést használta, és ebből a kifejezésből vezette le a függvény számos tulajdonságát.
Módosított Bessel-függvény
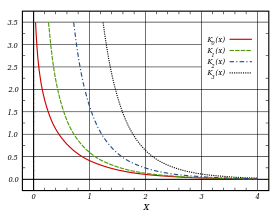
[szerkesztés]A Bessel-függvények érvényesek komplex argumentumú x-ekre is. Egy fontos speciális eset, amikor az argumentum tisztán komplex. Ezekben az esetekben a Bessel-függvény megoldásait módosított Bessel-függvényeknek hívják (vagy hiperbolikus Bessel-függvénynek).[1]

Irodalom
[szerkesztés]- Reiman István: Matematika. (hely nélkül): Typotex Kiadó. 2011. ISBN 978-963-279-300-9
- Lizorkin, P.I: Bessel function. (hely nélkül): Springer. 2001. ISBN 978-1-55608-010-4
Kapcsolódó szócikkek
[szerkesztés]- http://mathworld.wolfram.com/BesselFunction.html
- http://www.reak.bme.hu/fileadmin/user_upload/felhasznalok/kis/Bessel.pdf[halott link]
- http://dlmf.nist.gov/10
- Lommel-függvény
- Struve-függvény
- Hankel-függvény
- Anger-függvény
- Neumann-polinom
- Propagátor
Jegyzetek
[szerkesztés]- ↑ Abramowitz and Stegun, p. 375, 9.6.2, 9.6.10, 9.6.11.



