Árkuszszinusz-eloszlás

Az árkuszszinusz-eloszlás egy valószínűség-eloszlás, melynek a kumulatív eloszlásfüggvénye:

F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)={\frac {\arcsin(2x-1)}{\pi }}+{\frac {1}{2}}

a 0 ≤ x ≤ 1 tartományban, és a sűrűségfüggvénye:

f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}

(0,1) tartományban.

A standard árkuszszinusz-eloszlás a béta-eloszlás egy speciális esete, ahol α = β = 1/2. Ez azt jelenti, hogy ha $X$ egy standard árkuszszinusz-eloszlás, akkor $X\sim {\rm {Beta}}({\tfrac {1}{2}},{\tfrac {1}{2}})\$ .

Az árkuszszinusz-eloszlás megjelenik a következő törvényekben:

Kiterjesztés

Az eloszlás egy egyszerű transzformációval kiterjeszthető a ≤ x ≤ b tartományra:

F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {\frac {x-a}{b-a}}}\right)

ahol a ≤ x ≤ b, melynek a sűrűségfüggvénye:

f(x)={\frac {1}{\pi {\sqrt {(x-a)(b-x)}}}}

(a,b) tartományban.

Az árkuszszinusz-eloszlás jellemzői

Tartomány: $x\in [0,1]$
Sűrűségfüggvény: $f(x)={\frac {1}{\pi {\sqrt {x(1-x)}}}}$
Kumulatív eloszlásfüggvény: $F(x)={\frac {2}{\pi }}\arcsin \left({\sqrt {x}}\right)$
Átlag: ${\frac {1}{2}}$
Medián: ${\frac {1}{2}}$
módusz: $x\in {0,1}$
Szórásnégyzet: ${\tfrac {1}{8}}$
Ferdeség: $0$
Lapultság: $-{\tfrac {3}{2}}$

Jellemző görbék

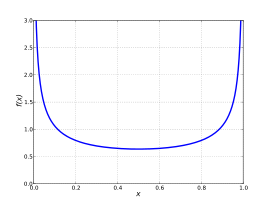
Jegyzetek

Források

Rogozin, B.A: Encyclopedia of Mathematics. (hely nélkül): Springer. 2001. ISBN 978-1-55608-010-4
Horváth Gézáné: Kvantitatív módszerek I.Fejezetek a valószínűségszámításból. (hely nélkül): PERFEKT ZRT. 2005. ISBN 9789633945902
Maddala, G.S: Limited-Dependent and Qualitative Variables in Econometrics. (hely nélkül): Cambridge University Press. 1983.
Tadikamalla, Pandu R: A Look at the Burr and Related Distributions. (hely nélkül): International Statistical Review 48 (3):. 1980. 337–344. o.
Burr, I.W: Cumulative frequency functions. (hely nélkül): Annals of Mathematical Statistics. 1942. 215–232. o.
Rodriguez, R.N: A guide to Burr Type XII distributions. (hely nélkül): Biometrika, 64. 1977. 129–134. o.

Kapcsolódó szócikkek