Szerkesztő:Thuluviel/Idézetek/provlog
A bizonyíthatósági logika a modális logika azon fejezete, amelyben egy modális kijelentés olyan módon igaz, hogy bizonyítható egy formális rendszerben, pl. egy (intuicionista) logikában, Peano-aritmetikában, halmazelméletben. A bizonyíthatósági logika célja tehát egy adott formális rendszerben a bizonyíthatóság-fogalom megragadása. A bizonyíthatóságot e nyelvben egy jellel szokás jelölni.
Példák
[szerkesztés]Intuicionista logika
[szerkesztés]Az intuicionista logikánál az egyik alkalmas fordítás úgy néz ki, hogy minden atomi mondat és negációjel elé egy -ot kell írni, így pl. egy, a kizárt harmadik elvét képviselő formula a következő alakot ölti:
Szóban mondva a „ állításnak rendelkezünk a bizonyításával, vagy a bizonyíthatóságának cáfolatával”. A modális logikából ismert lehetséges világok itt episztemikus helyzeteket képviselnek; a világban szereplő alakú formulák azok a formulák, melyeknek van bizonyításuk, azaz itt és már minden rákövetkező tudásállapotban rendelkezésünkre kell álljon az .
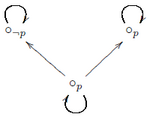
A fenti formula azonban a következő ábra (modális logikai modell) miatt hamis is lehet, így a kizárt harmadik törvényét képviselő formula nem logikai igazság - ami az intuicionista logikából valóban levezethetetlen. Ugyanis ha az alsó 'tudásállapotban' helyezkedik el a formula, akkor ez valóban hamis lesz, mivel egyrészt valóban nem igaz, hiszen a baloldali világban nem igaz, másrészt pedig sem igaz, mivel a jobboldali világnak minden rákövetkezőjében (azaz önmagában) igaz a .
Ez a fordítás a nulladrendű intuicionista logikát az S4 modális logikába fordította. Modális logikai szemszögből tehát azt mondhatjuk, hogy az S4 kalkulusnak két (adekvát) szemantikája lehetséges, az egyik a Kripke-szemantika, a másik pedig a nulladrendű intuicionista logika.
Peano-aritmetika
[szerkesztés]A Peano-aritmetika egy fordítása úgy néz ki, hogy a Peano-aritmetikában szereplő azon predikátumot, mely a levezethetőséget kódolja, írjuk át -ra. Mivel a Peano-aritmetikában lévő levezethetőségnek felel meg, így rajta keresztül itt is a bizonyíthatóságot ragadja majd meg.
A Peano-aritmetikára illeszkedő (Gödel és Löb után) GL modális logikában ha nézzük mondjuk a következő formulát:
Ez a formula, ha a fordítás tényleg jó, nem lehet tétel. Azt fejezi ugyanis ki, hogy „levezethető, hogy nem bizonyítható az ellentmondás”, azaz hogy bizonyítható az aritmetika konzisztenciája -- ennek azonban maga Gödel második nemteljességi tétele állja útját.
A GL-ről tehát majd azt mondhatjuk, hogy két szemantika adható rá; az egyik a szokásos Kripke-szemantika, a másik pedig maga a Peano-aritmetika.
Bizonyíthatósági logikák
[szerkesztés]Intuicionista logika
[szerkesztés]S4
[szerkesztés]| IPC lefordítása S4-re | ||
|---|---|---|
Gödel használta először a modális operátort bizonyíthatósági interpretációban, mikor 1933-ban kimutatta az intuicionista logikáról, hogy lefordítható C. I. Lewis egyik modális kalkulusába - ez a rendszer S4 volt.[1] Egy jó fordítás például az oldalt található (rekurzív) függvény.
Az ehhez hasonló fordítások felfedezése jelentős volt az intuicionisták számára is, hiszen a Kripke-szemantikák felfedezése után e fordítás megléte azt is jelentette, hogy S4 (adekvát) szemantikája szemantikája az intuicionista logikának is. Az intuicionizmus szokásos Kripke-szemantikája végülis nem S4 szemantikája lett, azaz a reflexív és tranzitív keretstruktúrák, hanem a reflexív, tranzitív és antiszimmetrikus keretstruktúrák, amelyekhez közel majd egy másik bizonyíthatósági logika, a Grz rendszer áll majd közel.
Grz
[szerkesztés]Peano-Aritmetika
[szerkesztés]GL
[szerkesztés]| GL lefordítása PA-ra | ||
|---|---|---|
A legfontosabb bizonyíthatósági modális rendszer, a GL rendszer (Gödel és Löb után) melyre a Kripke-féle (keretstruktúrás) szemantikán kívül egy alternatív szemantika is adható. Ez az alternatív - egyébként helyes és teljes - szemantika egy a Peano-aritmetika nyelvére való fordítás. A fordítás a -okhoz a Gödel számozást és a bizonyíthatósági predikátumot használja fel. Az oldalt látható táblázat megadja ezt a bizonyos szemantikát. A jelölés azt jelenti, hogy a aritmetikai formula levezethető -ból. Erről Gödel munkássága óta tudjuk, hogy ennek egy árnyéka, vetülete megjelenik nyelvében magában is: Vezessük be először is a függvényjelet. Ez egy trükkös módszerrel (lásd: Gödel-számozás) számokat rendel minden formulához. Ezt követően bevezetünk majd egy predikátumot, -et, amit a következőképpen definiálunk:
Azaz:
Ekkor a Gödel-tétel értelmében a következő - modális formuláink konstrukciójához hasonló konstrukcióval bíró - formulákra bukkanhatunk beszédünkben, miközben -ról tettünk a fenti módszerrel megállapításokat.
- Ha , akkor is.
Azaz, a könnyebb áttekinthetőség érdekében a helyébe -ot írva:
- Modális generalizáció: Ha , akkor is.
- K:
- tra :
- Löb :
A rendszer néhány érdekessége[2]:
- Az alternatívareláció irreflexív. (Az olyan keretstruktúraosztály, amely pontosan az irreflexív keretstruktúrákat tartalmazza, modálisan definiálhatatlan. A GL azonban erősebb rendszer így lehetséges, hogy minden modellje irreflexív.)
- A hozzá tartozó keretstruktúrák pontosan azok, amelyek tranzitívak és inverz jólfundáltak. Ez utóbbi a következő (ekvivalens kijelentéseket) jelenti:
- jólrendezett,
- nincsen szerint felszálló végtelen lánc.
- nincsenek világok, hogy
Ez utóbbi különösen azért érdekes, mert ez a tulajdonság elsőrendben már egyáltalán nem megfogalmazható. E tulajdonság az, ami miatt irreflexívek ugyanezen keretstruktúrák.
- nem tétele, de ez az előbbi tulajdonságból is következik.
- Nincsenek formájú tételei. Mint például a , azaz . Ez ugyanis olyasmit jelenthetne, hogy bizonyítható lenne, hogy a 0=1 állítás nem bizonyítható -- ez pedig szó szerint az aritmetika ellentmondásmentességének bizonyítása, ami a II. Gödel tétel értelmében nem lehetséges.
- tekintetében még a sem tétele GL-nek.
- viszont tétel.
- Viszont valahányszor tétele GL-nek egy formula, annyiszor tétele maga is. Ez Löb tételével cseng össze.
- Minden -beli formulának vannak fix pontjai: olyan mondatok, melyekre a diagonalizációs lemma alapján fennáll: .
- A predikátum fixpontja ez alapján: .
- Arra a kérdésre, hogy vajon bizonyítható-e ez, Löb adott egy választ (ez lenne Löb tétele): Ha , akkor .
- Ez utóbbit nyelvére átírva megkapjuk a W axiómát vagy Löb formulát:
- Löb: ,
- Löb:
| A GL kalkulus | |||
|---|---|---|---|
| Axiómák | Klasszikus | (A1) | |
| (A2) | |||
| (A3) | |||
| Modális | K | ||
| Löb | |||
| Levezetési szabályok: |
Klasszikus | (MP) | |
| Modális | (MG) | ||
Egy másik, sokkal fontosabb és érdekesebb bizonyíthatósági kalkulus a GL (Gödel és Löb után). Itt az állítások a Peano-aritmetika bizonyíthatóságára van illesztve. Bár ennek a Kripke-modelljei tranzitívak, nem feltétlen szükséges az ezt biztosító tra axióma -- ez ugyanis levezethető a GL kódú axiómából, ami a következő:
Ez az axióma Löb tételének felel meg.
GLS
[szerkesztés]Forrás
[szerkesztés]- szerk.: Solomon Feferman: Collected Works (angol, német nyelven). Oxford: Oxford University Press. ISBN 0-19-503964-5 (1986)
- George Boolos. The Logic of Provability. New York: Cambridge University Press (1993). ISBN 0-521-48325-5
Külső hivatkozások
[szerkesztés]- Sergei N. Artemov, Lev. D. Beklemishev. Provability Logic (angol nyelven), 174. o.












![{\displaystyle \scriptstyle {[p]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232e712cbd53cdf478ed58454e306cf52010f8f9)

![{\displaystyle \scriptstyle {[\lnot A]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34d141fbc57dc695d87236729221b6a906198aa4)
![{\displaystyle \scriptstyle {\Box \lnot [A]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc9029e9bea9a550b2f58121dfc2e213e5119a6c)
![{\displaystyle \scriptstyle {[A\rightarrow B]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/926cf799379d8d8d3897658411912153b5b70a67)
![{\displaystyle \scriptstyle {[A]\rightarrow [B]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35e962503e278d0764929aa51a2681ecadcc548e)
![{\displaystyle \scriptstyle {[A\vee B]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b901a86e8b6ccd4b22f4e6fee5f5f1513ae21345)
![{\displaystyle \scriptstyle {[A]\vee [B]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f035ba4dfb8c5cf3931bc6cdd03b35ef22c331bc)
![{\displaystyle \scriptstyle {[A\land B]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8afee2a893e349cc9e32cb3638754d9eddb861f)
![{\displaystyle \scriptstyle {[A]\land [B]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dad5788c7ef797d7a2e969e42461a653c127233c)
![{\displaystyle \scriptstyle {[\cdot ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2776aae759f571d65e026664acfef12e21c2add5)

![{\displaystyle \scriptstyle {\lnot [A]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fc0547d26aa569943b31c1425a0cb97d71672b5)
![{\displaystyle \scriptstyle {[\Box A]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b283ce6339004f6af61135d80342955cee1b354d)
![{\displaystyle \scriptstyle {Lev\,(\ulcorner [A]\urcorner )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f0f7abe5fa87181b49f9b60f8b73a08180b1926)








































