Szögmértékek

A síkszögek mérésére többféle mértékegységet használnak.

Fok - perc - másodperc

(SI-rendszerben az elnevezések : ívfok, ívperc, ívmásodperc )

A teljesszög illetve a körív 360 részre osztása évezredes babiloni örökség.
teljesszög = 360° (ívfok);
derékszög = 90°;
1° = 60' ;
1' = 60".
Megjegyzés: a 60-ados, más néven babiloni törteket használó egységek kisebb részeit egységesen szokás (magyarul) a perc, másod(ik)perc, harmad(ik)perc stb. megjelölésekkel illetni (v.ö.: óra-perc-másodperc).
Az egység választása kapcsolatba hozható a pí korai becslésével, ami szerint a kör kerülete a sugár 6-szorosa (az átmérő 3-szorosa). A körbe írt szabályos hatszög ismert szerkesztése sugallhatta a Q = $2\pi /6$ középponti szög egységként választását (a radián első közelítése) és az akkor már elterjedt 60-ados törtekkel a kisebb egységek ‒ a fok=Q/60, perc=fok/60; másodperc=perc/60 ‒ használatát.

A tengeri hajózásban használt tengeri mérföldet (ang.: nautical mile = NM) a Föld (korabeli) méretei alapján definiálták úgy, hogy 1 NM a földrajzi meridián 1'(perc)-es ívének a hossza.
Nincs kizárva, hogy az egység ilyen választása vezetett a 360-napos évet használó naptárak használatához: a Nap 1 nap alatt 1 fokot mozdul el a csillagképekhez viszonyítva.

Óra-perc-mp

A csillagászati számításoknál előnyös a Nap éves mozgásához hasonlóan a napi mozgást, a Föld teljes fordulatát követő szögmérték.
teljesszög = 24 h;
derékszög = 6 h;
1 h = 60 min;
1 min = 60 sec.

Fontos: Itt a min és sec jelöli a magyar perc és másodperc törtrészeket, az időmérés "óra" egységének 60-ados törtrészeit (babiloni törtek).

Újfok (gon)

A babiloni mértékek a 60-as számrendszert használják, ami a többi mennyiség decimális mértékével együtt a számítást nehezíti. Az újfok törtrészeit decimálisan képezzük. (Az SI-rendszer megengedi a nevesített törtrészek -cgon, mgon- használatát is.)

teljesszög = 400 gon;
derékszög = 100 gon;
1 gon = 100 cgon;
1 cgon =10 mgon.

Ez a szögmérték szorosan kapcsolódik a Föld méretével definiált méter-hez: a Föld (korabeli) méretei szerint a Földrajzi meridián 1 gon-os ívének hossza 100 km, vagy másképpen fogalmazva a délkör egy negyedének, azaz egy derékszögű, 100 gon-os ívének (meridián-quadráns) a hossza 10 000 km (v.ö.: tengeri mérföld).

Radián

(ívmérték) A szöghöz tartozó körív hosszának és a sugárnak a hányadosa az előző önkényesen választott mértékekkel ellentétben abszolút mértéket definiál. A gyakorlatban a Ludolph-féle szám irracionális volta miatt nem használható, de a tudományos számításokban, főként a trigonometrikus függvények és inverzeik használatához nélkülözhetetlen.

1 rad ~ 57,295° ~ 63,662 gon. teljesszög = 2π rad; derékszög = π/2 rad.

Vonás

A hadsereg vezette be gyakorlati haszna miatt.

Elméleti definíciója: 1000 vonás = 1 rad. Ezzel a teljes szög 2000π vonás ~ 6 283,185… vonás lenne, ami előnytelen. Ismert kerekítések:

A porosz, a K.u.K., majd a magyar hadseregben 1945-ig : teljesszög = 64-00, (olv. hatvannégy-nullanulla).

Az orosz, majd a szovjet és 1945 után a csatlós államokban: a teljesszög = 60-00, a derékszög = 15-00.

A vonás-mérték jellemzője, hogy 1 km távolságban lévő 1 m hosszú tárgynak 1 vonás a látószöge. Az ismert méretű objektumok látószögének lemérésével a távolsága, a távolságának ismeretében mérete becsülhető. Méret = látószög × távolság, az adott egységekben.

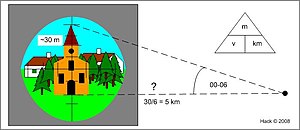
További előny, hogy a szögfüggvények becslése is egyszerűsödik.

A "hozzárendelés" így szól: a sinus 10-00-ig a vonás 1000-ed része, e fölött = 1.

1. Példa: 30° = 05-00, szinusza = 0.5 mindkét számítás szerint.

2. Példa: 45° = 07-50, sin45° = 0,6947 ~ 0,7 illetve (07-50):1000 ~ 0,75.

Hajózási vonás

Iránytűrózsa a 32 vonásegységgel

A vitorlások korában az iránytű alatti skála (anemona, szélrózsa) legkisebb egysége. Használatát a korabeli mágneses iránytűk és a hajók irányításának bizonytalansága indokolja.

1 hv. = 11°15' = 11,25°

teljesszög = 32 hv;

derékszög = 8 hv.

Források

• Négyjegyű függvénytáblázatok, összefüggések és adatok - Nemzeti Tankönyvkiadó, Budapest, 2005
• Pattantyús: Matematikai képletek, táblázatok - Műszaki Kiadó, Budapest, 1961
• Steiner: Sphärische Trigonometrie - Teubner, Leipzig, 1977.