Prímszámláló függvény

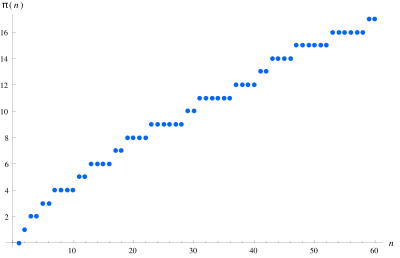
A matematika, azon belül az analitikus számelmélet területén a prímszámláló függvény (prime-counting function) az a számelméleti függvény, ami az x valós számnál nem nagyobb prímszámok számát adja meg. Jelölése π(x) (nincs közvetlen köze a pí számhoz).

π(n) értékei az első 60 egész számra

Története

A számelmélet kutatóinak érdeklődésére régóta számot tart a prímszámláló függvény növekedési rátája. A 18. század végén Gauss és Legendre megsejtette, hogy értéke kb.

$x/\operatorname {ln} (x)\!,$

abban az értelemben, hogy

$\lim _{x\rightarrow \infty }{\frac {\pi (x)}{x/\operatorname {ln} (x)}}=1.\!$

Ezt az állítást ma prímszámtételként ismerjük. Ezzel ekvivalens állítás, hogy

$\lim _{x\rightarrow \infty }\pi (x)/\operatorname {li} (x)=1\!,$

ahol li a logaritmikus integrál függvény. A prímszámtételt 1896-ban egymástól függetlenül Jacques Hadamard és Charles de la Vallée Poussin is bebizonyította, a Riemann által 1859-ben bevezetett Riemann-féle zéta-függvény tulajdonságainak felhasználásával.

Azokban a nagyságrendekben, amelyekben a számelmélet általában vizsgálódik (tehát amikor $x$ nem kezelhetetlenül nagy), $\operatorname {li} (x)\!$ nagyobb, mint $\pi (x)\!$, de végtelen sokszor igaz ennek az ellenkezője is. Ennek tárgyalását lásd a Skewes-féle szám szócikkben.

A prímszámtétel olyan bizonyítását, ami nem használta sem a zéta-függvényt, sem a komplex analízis eszköztárát 1948-ban adta Atle Selberg és Erdős Pál (nagyrészt egymástól függetlenül).

Táblázat π(x), x / ln x és li(x) értékeivel

A táblázat a három függvény, π(x), x / ln x és li(x) értékeit mutatja meg 10 különböző hatványainál. Lásd még és

x	π(x)	π(x) − x / ln x	li(x) − π(x)	x / π(x)
10	4	−0,3	2,2	2,500
102	25	3,3	5,1	4,000
103	168	23	10	5,952
104	1 229	143	17	8,137
105	9 592	906	38	10,425
106	78 498	6 116	130	12,740
107	664 579	44 158	339	15,047
108	5 761 455	332 774	754	17,357
109	50 847 534	2 592 592	1 701	19,667
1010	455 052 511	20 758 029	3 104	21,975
1011	4 118 054 813	169 923 159	11 588	24,283
1012	37 607 912 018	1 416 705 193	38 263	26,590
1013	346 065 536 839	11 992 858 452	108 971	28,896
1014	3 204 941 750 802	102 838 308 636	314 890	31,202
1015	29 844 570 422 669	891 604 962 452	1 052 619	33,507
1016	279 238 341 033 925	7 804 289 844 393	3 214 632	35,812
1017	2 623 557 157 654 233	68 883 734 693 281	7 956 589	38,116
1018	24 739 954 287 740 860	612 483 070 893 536	21 949 555	40,420
1019	234 057 667 276 344 607	5 481 624 169 369 960	99 877 775	42,725
1020	2 220 819 602 560 918 840	49 347 193 044 659 701	222 744 644	45,028
1021	21 127 269 486 018 731 928	446 579 871 578 168 707	597 394 254	47,332
1022	201 467 286 689 315 906 290	4 060 704 006 019 620 994	1 932 355 208	49,636
1023	1 925 320 391 606 803 968 923	37 083 513 766 578 631 309	7 250 186 216	51,939
1024	18 435 599 767 349 200 867 866	339 996 354 713 708 049 069	17 146 907 278	54,243
1025	176 846 309 399 143 769 411 680	3 128 516 637 843 038 351 228	55 160 980 939	56,546
1026	1 699 246 750 872 437 141 327 603	28 883 358 936 853 188 823 261	155 891 678 121	58,850

A grafikon a π(x) prímszámláló függvény két közelítéséhez, az x/ln x-hez és a Li(x)-hez való arányát mutatja. Az x növekedésével (vegyük észre, hogy az x tengely logaritmikus beosztású), mindkét arány 1-hez tart. Az x/ln x felülről konvergál, viszonylag lassan, míg az Li(x) alulról, gyorsabban.

Az On-Line Encyclopedia of Integer Sequences között a π(x) oszlop megtalálható  A006880, a π(x) − x / ln x oszlop a  A057835 és a li(x) − π(x) oszlop pedig a  A057752 sorozatnál.

A π(10²⁴)-nél szereplő értéket először J. Buethe, J. Franke, A. Jost és T. Kleinjung számolta ki a Riemann-sejtés igazát feltételezve. Ezt a számítást később a feltétel nélkül is elvégezte D. J. Platt. A π(10²⁵) értéket J. Buethe, J. Franke, A. Jost és T. Kleinjung, a π(10²⁶) értéket pedig D. B. Staple számolta ki. A táblázat többi értékét a fenti munka során ellenőrizték.

Algoritmusok a π(x) értékének meghatározására

Triviális módja $\pi (x)$ meghatározásának, ha $x$ nem túl nagy, hogy meghatározzuk az $x$-nél nem nagyobb prímeket (akár Eratoszthenész szitájával), majd megszámoljuk őket.

Legendre kifinomultabb módszert talált $\pi (x)$ kiszámolására: adott $x$-re, ha $p_{1},p_{2},\ldots ,p_{n}$ különböző prímszámok, akkor az olyan egészek száma, melyek nem nagyobbak $x$-nél és nem oszthatók egyetlen $p_{i}$-vel sem, éppen

$\lfloor x\rfloor -\sum _{i}\left\lfloor {\frac {x}{p_{i}}}\right\rfloor +\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor -\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor +\cdots$

(ahol $\lfloor \cdots \rfloor$ az alsó egészrész függvényt jelöli). A szám tehát egyenlő a következővel:

$\pi (x)-\pi \left({\sqrt {x}}\right)+1,$

ahol a $p_{1},p_{2},\ldots ,p_{n}$ számok az $x$ négyzetgyökénél nem nagyobb prímszámok.

1870 és 1885 között megjelent cikksorozatában Ernst Meissel bemutatott egy praktikus kombinatorikai módszert $\pi (x)$ kiszámolására. Legyen $p_{1}$, $p_{2},\ldots ,p_{n}$ az első $n$ prímszám, jelölje $\Phi (m,n)$ az $m$-nél nem nagyobb természetes számokat, melyek nem oszthatók egyik $p_{i}$-vel sem. Ekkor

$\Phi (m,n)=\Phi (m,n-1)-\Phi \left({\frac {m}{p_{n}}},n-1\right)$

Adott $m$ természetes számra, ha $n=\pi \left({\sqrt[{3}]{m}}\right)$ és $\mu =\pi \left({\sqrt {m}}\right)-n$, akkor

$\pi (m)=\Phi (m,n)+n(\mu +1)+{\frac {\mu ^{2}-\mu }{2}}-1-\sum _{k=1}^{\mu }\pi \left({\frac {m}{p_{n+k}}}\right)$

Ezt a megközelítést használva Meissel kiszámította $\pi (x)$-et az $x$ egyenlő 5·10⁵, 10⁶, 10⁷ és 10⁸ értékekre.

1959-ben Derrick Henry Lehmer kiterjesztette és egyszerűsítette Meissel módszerét. Az $m$ valós számra és az $n$ és $k$ természetes számokra definiáljuk $P_{k}(m,n)$-et úgy, hogy az m-nél nem nagyobb, de pontosan k darab, $p_{n}$-nél nagyobb prímtényezővel rendelkező számok számát adja. Továbbá, legyen $P_{0}(m,n)=1$. Ekkor

$\Phi (m,n)=\sum _{k=0}^{+\infty }P_{k}(m,n),$

ahol valójában csak véges számú nem nulla tagot összegzünk. Jelöljön $y$ olyan egész számot, amire igaz, hogy ${\sqrt[{3}]{m}}\leq y\leq {\sqrt {m}}$, és $n$-et állítsuk $n=\pi (y)$ értékre. Ekkor $P_{1}(m,n)=\pi (m)-n$ és $P_{k}(m,n)=0$, ha $k$ ≥ 3. Emiatt

$\pi (m)=\Phi (m,n)+n-1-P_{2}(m,n).$

A $P_{2}(m,n)$ értéke így számítható:

$P_{2}(m,n)=\sum _{y<p\leq {\sqrt {m}}}\left(\pi \left({\frac {m}{p}}\right)-\pi (p)+1\right).$

Másrészről, a $\Phi (m,n)$ kiszámítása elvégezhető a következő szabályok alapján:

1. $\Phi (m,0)=\lfloor m\rfloor$
2. $\Phi (m,b)=\Phi (m,b-1)-\Phi \left({\frac {m}{p_{b}}},b-1\right)$

Ezzel a módszerrel és egy IBM 701 elektroncsöves számítógéppel Lehmer képes volt kiszámítani $\pi \left(10^{10}\right)$ értékét.

A módszert a későbbiekben Lagarias, Miller, Odlyzko, Deléglise és Rivat tökéletesítették.

Más prímszámláló függvények

Definiáltak más prímszámláló függvényeket is, melyekkel bizonyos feladatok kényelmesebben elvégezhetők. Az egyik ilyen a Riemann-féle prímszámláló függvény, aminek jelölése $\Pi _{0}(x)$ vagy $J_{0}(x)$. Ez a függvény a pⁿ prímhatványoknál 1/n ugrásokat végez, a nem prímhatvány helyeken pedig a két szélső prímhatvány átlagát veszi fel. Ennek az az értelme, hogy a függvény értéke meghatározható egy inverz Mellin-transzformációval. Szabatosan a $\Pi _{0}(x)$ így definiálható:

$\Pi _{0}(x)={\frac {1}{2}}{\bigg (}\sum _{p^{n}<x}{\frac {1}{n}}\ +\sum _{p^{n}\leq x}{\frac {1}{n}}{\bigg )},$

ahol p prímszám.

Így is felírható:

$\Pi _{0}(x)=\sum _{2}^{x}{\frac {\Lambda (n)}{\ln n}}-{\frac {1}{2}}{\frac {\Lambda (x)}{\ln x}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\pi _{0}(x^{1/n}),$

ahol Λ(n) a von Mangoldt-függvény és

$\pi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\pi (x-\varepsilon )+\pi (x+\varepsilon )}{2}}.$

A Möbius-féle megfordítási formula ekkor kiadja, hogy:

$\pi _{0}(x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi _{0}(x^{1/n})$

A Riemann-féle zéta-függvény logaritmusának és a von Mangoldt-függvény $\Lambda$ ismeretében, a Perron-képlet felhasználásával:

$\ln \zeta (s)=s\int _{0}^{\infty }\Pi _{0}(x)x^{-s-1}\,dx$

A Csebisev-függvények a prímeket vagy pⁿ prímhatványokat ln(p)-vel súlyozva összegeznek:

$\theta (x)=\sum _{p\leq x}\ln p$

$\psi (x)=\sum _{p^{n}\leq x}\ln p=\sum _{n=1}^{\infty }\theta (x^{1/n})=\sum _{n\leq x}\Lambda (n).$

Prímszámláló függvények képletei

A prímszámláló függvényképletek kétfajták lehetnek: számelméleti és analitikus formulák. Az analitikus prímszámlálási képleteket először a prímszámtétel bizonyítására használták. Riemann és von Mangoldt munkásságából erednek, és általában explicit formuláknak nevezik őket.

Van tehát a következő képletünk ψ-re:

$\psi _{0}(x)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-\ln 2\pi -{\frac {1}{2}}\ln(1-x^{-2})$

ahol

$\psi _{0}(x)=\lim _{\varepsilon \rightarrow 0}{\frac {\psi (x-\varepsilon )+\psi (x+\varepsilon )}{2}}.$

Itt ρ a Riemann-féle zéta-függvény zérushelyei a kritikus sávban, ahol a ρ valós része 0 és 1 közé esik. A képlet érvényes az x>1 értékekre, ami az érdekes terület. A gyökök összege feltételesen konvergens, és a képzetes rész növekvő abszolút értékének sorrendjében kell elvégezni az összegzést. Vegyük észre, hogy ugyanez az összeg a triviális gyökökön elvégezve a képlet utolsó kivonandóját adja.

A $\scriptstyle \Pi _{0}(x)$-re bonyolultabb képletünk van:

$\Pi _{0}(x)=\operatorname {li} (x)-\sum _{\rho }\operatorname {li} (x^{\rho })-\ln 2+\int _{x}^{\infty }{\frac {dt}{t(t^{2}-1)\ln t}}.$

Itt is az látható, hogy a képlet érvényes x > 1-re, ahol ρ a zéta-függvény nem triviális zérushelyei abszolút értékeik szerint rendezve, a második integrál, negatív előjellel, pedig ugyanaz az összeg, csak a triviális zérushelyeken. Az első tag li(x)-e a szokásos logaritmikus integrálfüggvény; a második tag li(x^ρ) kifejezését úgy kell érteni, mint Ei(ρ ln x), ahol Ei a pozitív valós számokon értelmezett exponenciális integrál függvény analitikus folytatása a komplex síkra, a negatív valós számok tengelyén.

Így a Möbius-féle megfordítási formula kiadja, hogy

$\pi _{0}(x)=\operatorname {R} (x)-\sum _{\rho }\operatorname {R} (x^{\rho })-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}$

ami x > 1-re van értelmezve, és ahol

$\operatorname {R} (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {li} (x^{1/n})=1+\sum _{k=1}^{\infty }{\frac {(\ln x)^{k}}{k!k\zeta (k+1)}}$

az úgynevezett Riemann-féle R-függvény. Ez utóbbi sort Gram-sornak nevezik és minden pozitív x-re konvergens.

Δ-függvény (pirossal) logaritmikus léptékben

A $\scriptstyle \pi _{0}(x)$ képletében a nem triviális zérushelyek összege $\scriptstyle \pi _{0}(x)$ fluktuációit írja le, a maradék tagok pedig a prímszámláló függvény „sima” részét alkotják, így használható a

$\operatorname {R} (x)-{\frac {1}{\ln x}}+{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}$

képlet a $\scriptstyle \pi (x)$ legjobb becsléseként az x > 1 értékekre.

A „zajos” rész amplitúdója heurisztikusan $\scriptstyle {\sqrt {x}}/\ln x$ körül van, így a prímszámok eloszlásának fluktuációi megjeleníthetők a Δ-függvény segítségével:

$\Delta (x)=\left(\pi _{0}(x)-\operatorname {R} (x)+{\frac {1}{\ln x}}-{\frac {1}{\pi }}\arctan {\frac {\pi }{\ln x}}\right){\frac {\ln x}{\sqrt {x}}}.$

A Δ(x) különböző helyeken vett értéket tartalmazó táblázat elérhető.

Egyenlőtlenségek

Néhány hasznos egyenlőtlenség π(x)-szel kapcsolatban.

${\frac {x}{\ln x}}<\pi (x)<1,25506{\frac {x}{\ln x}}\!$ ha x ≥ 17.

A bal oldali egyenlőtlenség minden x ≥ 17-re, a jobb oldali egyenlőtlenség minden x > 1-re teljesül.

Az 1,25506 konstans magyarázata itt olvasható: (A209883 sorozat az OEIS-ben).

Pierre Dusart igazolta 2010-ben, hogy:

${\frac {x}{\ln x-1}}<\pi (x)$, ha $x\geq 5393$ és

$\pi (x)<{\frac {x}{\ln x-1,1}}$, ha $x\geq 60184$.

Néhány az n-edik prímszámra, p_n-re vonatkozó egyenlőtlenség.

$n(\ln(n\ln n)-1)<p_{n}<n{\ln(n\ln n)}\!$ ha n ≥ 6.

A bal oldali egyenlőtlenség minden n ≥ 1-re, a jobb oldali minden n ≥ 6-ra teljesül.

Az n-edik prímszám közelítő értéke:

$p_{n}=n(\ln(n\ln n)-1)+{\frac {n(\ln \ln n-2)}{\ln n}}+O\left({\frac {n(\ln \ln n)^{2}}{(\ln n)^{2}}}\right).$

Jól ismert jegyzetfüzetében Rámánudzsan bizonyítja, hogy a

$\pi (x)^{2}<{\frac {ex}{\log x}}\pi {\bigg (}{\frac {x}{e}}{\bigg )}$

egyenlőtlenség teljesül $x$ elegendően nagy értékeire.

A Riemann-sejtés

A Riemann-sejtés megfelel a $\pi (x)$-re való becslés sokkal szigorúbb hibakorlátjának, és így a prímszámok szabályosabb eloszlásának:

$\pi (x)=\operatorname {li} (x)+O({\sqrt {x}}\log {x}).$

Specifikusan,

$|\pi (x)-\operatorname {li} (x)|<{\frac {1}{8\pi }}{\sqrt {x}}\,\log {x},\qquad {\text{ha }}x\geq 2657.$

Kapcsolódó szócikkek

• Bertrand-posztulátum
• Oppermann-sejtés
• Foias-állandó

További információk

• Chris Caldwell, The Nth Prime Page at The Prime Pages.
• Tomás Oliveira e Silva, Tables of prime-counting functions.