Szögátmérő

A szögátmérő (más néven látszólagos átmérő) egy objektum látszó átmérőjének szögmértékben kifejezett értéke. A geometriában látószögnek hívják.

Kiszámítása

Diagram a szögátmérő kiszámításához

Közelebb lévő kisebb és távolabb lévő nagyobb égitestek azonos szögátmérőjűek lehetnek

$\delta =2\arctan \left({\frac {1}{2}}{\frac {d}{D}}\right).$

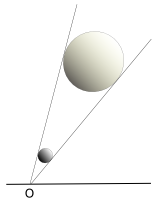
Ha ismerjük a szögátmérőt (δ) és a test átmérőjét (d), akkor meghatározható a távolsága (D), vagy pedig ha a távolságát ismerjük, akkor az átmérője. Széleskörűen alkalmazott mérték a csillagászatban.

A Nap és a Hold szögátmérője csaknem azonos (kb. fél fok, azaz 30 ívperc, ami 1800 ívmásodperc). A bolygók közül általában a Jupiteré a legnagyobb (30″–50″), bár néha a Vénuszé (9,5″–66″), ezután következik a Szaturnusz (15″-21″), a Mars (3,5″–25″), a Merkúr (4,5″–13″). A Pluto csak 6 század és egy tized ívmásodperces szögátmérő alatt látszik. Az egyik legnagyobb ismert csillag, a Betelgeuze szögátmérője kb. 0,05″.

Geometriája

A kerületi és középponti szögek tétele levezethető, hogy egy adott szakasz pontjai két körív pontjaiból láthatók azonos szög alatt. Ez a látószög tétele. Ha a szög hegyesszög, akkor az ívek félkörnél hosszabbak; ha tompaszög, akkor félkörnél rövidebbek. Ha derékszög, akkor a két körív félkör, amik együtt éppen a Thalész-kört adják ki. A köríveken belülről a szakasz az adott szögnél nagyobb, rajta kívül kisebb szög alatt látszódik.

A látószögkörív szerkesztése:

• Jelölje az adott szöget α! Betűzzük a szakasz végpontjait A-val és B-vel!
• A szakasz felezőmerőlegese tartalmazza a körív (k) középpontját (K).
• Az A (vagy a B) pontba másoljuk α-t.
• Az új szögszárra a szakasz végpontjában emelt merőleges kimetszi a szakasz felezőmerőlegeséből a középpontot.
• Ezután a középpontból felmérve a középpont és a szakasz végpontjának távolságát behúzható a körív.
• A körívet a szakasz egyenesére tükrözve megkapjuk a másik látószögkörívet.

Alkalmazása

A látószögkörívet felhasználják több matematikai tételhez is:

• Húrnégyszögek tétele
• Thalész-tétel
• Szelőtétel
• Összefüggés a háromszög egyik szöge, az azzal szemközti oldal és a háromszög köré írt kör sugara között

Továbbá felhasználják képalkotáshoz, fényképezéshez és a csillagászatban.