Gram–Schmidt-eljárás

A főként a lineáris algebrában és a numerikus analízisben használatos Gram–Schmidt-ortogonalizálás (avagy Gram–Schmidt-eljárás, esetleg Gram–Schmidt-féle ortogonalizálási eljárás) egy skalárszorzatos tér egy véges, lineárisan független {v_j} vektorrendszerét alakítja át egy olyan {u_j} vektorrendszerré, melynek elemei páronként merőlegesek egymásra (a skalárszorzatra vonatkozóan), más szóval ortogonálisak, és a két vektorrendszer ugyanazt az alteret feszíti ki az említett skalárszorzatos térben.

A módszert Jørgen Pedersen Gram és Erhard Schmidt után nevezték el, bár korábban Laplace-nál is szerepelt az eljárás. A Gram–Schmidt-ortogonalizálás egy általánosításának tekinthető a Lie-csoportok elméletében szereplő Iwasawa-dekompozíció.

Az eljárás alkalmazható például a reguláris mátrixok QR-felbontásánál.

Lebegőpontos számításokhoz kevéssé alkalmas, mivel a felhalmozódó kerekítési hibák miatt a kapott vektorok nem lesznek ortogonálisak. Egyes módosítások kiküszöbölik ezt a hibát, így alkalmassá téve a módszert ezekre a számításokra.

A Gram–Schmidt-eljárás

Az egydimenziós altérre vetítés

Pre-Hilbert-térben (skalárszorzatos térben) az u nemnulla vektor alterébe merőlegesen vetít a

$\mathrm {proj} _{\mathbf {u} }\,\mathbf {x} =\langle \mathbf {u} ,\mathbf {x} \rangle {\frac {\mathbf {u} }{\|\mathbf {u} \|^{2}}}$

leképezés, ahol <u, x> a két vektor skaláris szorzatát jelöli. A projekciótételből következik ugyanis, hogy pre-Hilbert-térben, ha létezik olyan y vektor az u kifeszítette altérben, hogy minden λ ∈ C(ill. R)-re

$\|\mathbf {x} -\mathbf {y} \|\leq \|\mathbf {x} -\lambda .\mathbf {u} \|\,$

akkor az ilyen y-t egyértelműen jellemzi az, hogy minden λ ∈ C (illetve R)-re:

$\langle \mathbf {x} -\mathbf {y} ,\lambda .\mathbf {u} \rangle =0$

És valóban létezik ilyen y éspedig pont a fenti projekció, ugyanis

$\left\langle \mathbf {x} -\langle \mathbf {u} ,\mathbf {x} \rangle {\frac {\mathbf {u} }{\|\mathbf {u} \|^{2}}},\lambda .\mathbf {u} \right\rangle =\langle \mathbf {x} ,\lambda .\mathbf {u} \rangle -\langle \mathbf {u} ,\mathbf {x} \rangle {\frac {\lambda .\mathbf {u} ^{2}}{\|\mathbf {u} \|^{2}}}=\langle \mathbf {x} ,\lambda .\mathbf {u} \rangle -\langle \lambda .\mathbf {u} ,\mathbf {x} \rangle \cdot 1=0$

Az eljárás

A Gram–Schmidt-eljárás első lépése: vetítsük merőlegesen v₂-t v₁-re. Ekkor Span(v₁,v₂) = Span(v₁,v₂ - proj v₂) és az utóbbiak merőlegesek.

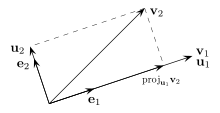
Legyen {v₁, ... , v_n } lineárisan független vektorrendszer. Azt az {u₁, ... , u_n } vektorrendszert, melynek elemei páronként merőlegesek és Span(v₁, ... , v_n) = Span(u₁, ... , u_n) (azaz ugyanazt az alteret feszítik ki, ugyanaz a generált Span(...) részalgebrájuk) a következőképpen kapjuk. Legyen u₁=v₁. Vetítsük v₂-t merőlegesen u₁-re, legyen ez w₂. Ekkor u₂ = v₂ – w₂. Tegyük ezt v₃-mal és u₁-vel illetve u₂-vel ... Ha ortonormált bázist akarunk, akkor osszuk le az u_k-kat a hosszukkal.

	$\mathbf {u} _{1}=\mathbf {v} _{1},$		$\mathbf {e} _{1}={\mathbf {u} _{1} \over \|\mathbf {u} _{1}\|}$
	$\mathbf {u} _{2}=\mathbf {v} _{2}-\mathrm {proj} _{\mathbf {u} _{1}}\,\mathbf {v} _{2},$		$\mathbf {e} _{2}={\mathbf {u} _{2} \over \|\mathbf {u} _{2}\|}$
	$\mathbf {u} _{3}=\mathbf {v} _{3}-\mathrm {proj} _{\mathbf {u} _{1}}\,\mathbf {v} _{3}-\mathrm {proj} _{\mathbf {u} _{2}}\,\mathbf {v} _{3},$		$\mathbf {e} _{3}={\mathbf {u} _{3} \over \|\mathbf {u} _{3}\|}$
	$\mathbf {u} _{4}=\mathbf {v} _{4}-\mathrm {proj} _{\mathbf {u} _{1}}\,\mathbf {v} _{4}-\mathrm {proj} _{\mathbf {u} _{2}}\,\mathbf {v} _{4}-\mathrm {proj} _{\mathbf {u} _{3}}\,\mathbf {v} _{4},$		$\mathbf {e} _{4}={\mathbf {u} _{4} \over \|\mathbf {u} _{4}\|}$
	$\vdots$		$\vdots$
	$\mathbf {u} _{n}=\mathbf {v} _{n}-\sum _{k=1}^{n-1}\mathrm {proj} _{\mathbf {u} _{k}}\,\mathbf {v} _{n},$		$\mathbf {e} _{n}={\mathbf {u} _{n} \over \|\mathbf {u} _{n}\|}$

Helyesség

Annak az igazolása, hogy az eljárás valóban a kívánt eredményt adja a következő.

Először belátjuk, hogy az {u_k} vektorrendszer bázisa a {v_k} vektorrendszer által kifeszített L lineáris altérnek. Mivel L dimenziója a feltevés miatt éppen |{v_k}| = n, ezért elég belátni, hogy {u_k} generálja L-et. Tudjuk:

$\mathbf {u} _{1}=\mathbf {v} _{1}$

$\mathbf {u} _{2}=\mathbf {v} _{2}-\lambda _{21}\mathbf {u} _{1}$

$\mathbf {u} _{3}=\mathbf {v} _{3}-\lambda _{32}\mathbf {u} _{2}-\lambda _{31}\mathbf {u} _{1}$

$\vdots$

$\mathbf {u} _{n}=\mathbf {v} _{n}-\sum _{k=1}^{n-1}\lambda _{nk}{\mathbf {u} _{k}}$

alkalmas λ_ij számokkal. Valójában tetszőleges λ_ij-kre generálja {u_k} az L-et, mert minden k-ra v_k előáll az u₁, ... , u_k-k lineáris kombinációjaként, azaz előállítják az összes bázisvektort, melyek viszont előállítják L összes elemét.

Másodszor belátjuk, hogy minden k = 1, ..., n-re az algoritmus által előállított {u₁,...,u_k} ortogonális, azaz

$\langle \mathbf {u} _{i},\mathbf {u} _{j}\rangle \left\{{\begin{matrix}\neq 0,&\mathrm {ha} &i=j\\=0,&\mathrm {ha} &i\neq j\end{matrix}}\right.$

k=1 esetén az egyetlen nemnulla u teljesíti az ortogonalitási kritériumot. Ha 1, ..., k–1 már teljesíti a páronkénti ortogonalitást, akkor az u_k vektor mindegyik addigira merőleges, mert

$\langle \mathbf {u} _{i},\mathbf {u} _{k}\rangle =\langle \mathbf {u} _{i},\mathbf {v} _{k}-\sum _{j=1}^{k-1}\lambda _{kj}{\mathbf {u} _{j}}\rangle =\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle -\sum _{j=1}^{k-1}\lambda _{kj}\langle \mathbf {u} _{i},\mathbf {u} _{j}\rangle =$

$=\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle -\lambda _{ki}\langle \mathbf {u} _{i},\mathbf {u} _{i}\rangle =\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle -{\frac {\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle }{\|\mathbf {u} _{i}\|^{2}}}\langle \mathbf {u} _{i},\mathbf {u} _{i}\rangle =0$,

hiszen az algoritmusból kiolvasva éppen

$\lambda _{ki}={\frac {\langle \mathbf {u} _{i},\mathbf {v} _{k}\rangle }{\|\mathbf {u} _{i}\|^{2}}}\,$.

Megjegyzések

• Az eljárás általános k-adik lépésének formuláját így is írhatjuk:

$\mathbf {v} _{k}=\mathbf {u} _{k}+\sum _{i=1}^{k-1}\mathrm {proj} _{\mathbf {u} _{i}}\,\mathbf {v} _{k}$.

Eszerint ha már megvan az {u₁, ..., u_k–1} ortogonális rendszer, akkor a k-adik lépésben nem mást teszünk, mint vesszük a v_k vektor új, már meglévő báziselemekre eső merőleges vetületét és kiválasztjuk, hogy melyik u_k vektor az, amelyiket a vetületekhez adva v_k előáll. Míg a projekciótétel, lévén tiszta egzisztenciatétel, csak azt állítja, hogy létezik ilyen vektor, addig a Gram–Schmidt-eljárás konstruktívan adja meg a vetületet, éspedig:

$\mathbf {m} _{0}=\mathbf {v} _{k}-\mathbf {u} _{k}=\sum _{i=1}^{k-1}\mathrm {proj} _{\mathbf {u} _{i}}\,\mathbf {v} _{k}$.

A helyességi gondolatmenetben pont azt látjuk be, hogy a v_k – m₀ vektor merőleges a Span({u₁, ..., u_k–1}) altérre, hisz mindegyik bázisvektorára merőleges.

• Végtelen dimenziós altér esetén szintén alkalmazható az eljárás, azzal az eredménnyel, hogy az előállított (u₁, ..., u_k, ...) sorozatban bármely k-ig az u₁, ..., u_k vektorok páronként ortogonálisak. Itt a függetlenség azt jelenti, hogy egy elem sem fekszik a korábbiak lineáris burkában. Megszámlálható esetben (szeperábilis Hilbert-terekben) az ortogonalizáció visszavezethető véges esetre. Általában minden független rendszer a jólrendezési tétel szerint felírható egy $\left(\mathbf {w} _{\alpha }\right)_{\alpha <d}$ sorozatként, ahol $d$ kardinális szám, és $\alpha$ ordinális szám. Ha a rendszer lineáris burka sűrű, akkor $d$ a Hilbert-tér dimenziója. Jelölje $H$ a teret, és legyen $\pi _{A}\colon H\to A$ egy ortogonális projekció az $A$ altérre, ami a teljesség miatt mindig létezik, és ${\hat {\mathbf {x} }}$ legyen az $\textstyle {\frac {\mathbf {x} }{\left\|\mathbf {x} \right\|}}$ normált vektor. Így adódik egy $\left(\mathbf {v} _{\alpha }\right)_{\alpha <d}$ ortonormált rendszer, ahol

$A_{\alpha }:={\overline {\operatorname {span} \left(\left\{\mathbf {w} _{\beta }\colon \beta <\alpha \right\}\right)}}$

$\mathbf {v} _{\alpha }:={\widehat {\left(\mathbf {w} _{\alpha }-\pi _{A_{\alpha }}\left(\mathbf {w} _{\alpha }\right)\right)}}$.

• Transzfinit indukcióval megmutatható, hogy $A_{\alpha }={\overline {\operatorname {span} \left(\left\{\mathbf {v} _{\beta }\colon \beta <\alpha \right\}\right)}}$, továbbá $\alpha =d$. Explicit transzfinit rekurzióval:

$\mathbf {v} _{\alpha }:={\widehat {\left(\mathbf {w} _{\alpha }-\sum _{\beta <\alpha }\langle \mathbf {v} _{\beta },\mathbf {w} _{\alpha }\rangle \cdot \mathbf {v} _{\beta }\right)}}$

A Bessel-egyenlőtlenség miatt az összeg jóldefiniált (legfeljebb megszámlálható sok elem különbözik nullától).

• Lineárisan összefüggő vektorrendszerre alkalmazva az eljárást az eredményben előbb-utóbb előáll a 0 vektor. Ha ugyanis a k-adik vektor már az előzőek által kifeszített altérben van, akkor a vektorból az altérre eső vetületét kivonva a 0-t kapjuk. A lineárisan összefüggő vektorok által kifeszített alteret is lehet azonban ortogonális vektorokkal előállítani, éspedig úgy, hogy az algoritmusban minden új bázisvektor esetén megnézzük, hogy 0-t ad-e és ha igen, a régi vektort elvetjük és folytatjuk egy másik elem előállításával. Ekkor az algoritmus eredménye annyi vektor lesz, amennyi az eredeti vektorrendszer rangja volt.

• Az eljárás alatt az addig kiszámolt $\mathbf {v} _{1},\dots ,\mathbf {v} _{i}$ vektorok ugyanazt az alteret feszítik ki, mint az eredeti $\mathbf {w} _{1},\dots ,\mathbf {w} _{i}$ vektorok. A $\mathbf {v} _{1},\dots ,\mathbf {v} _{i}$ vektorok ortogonális bázist alkotnak a megfelelő altérben. Más szóval, az egyik rendszert a másik rendszer bázisában jobb felső háromszögmátrix fejezi ki. Ennek a mátrixnak pozitív a determinánsa, így az eredményként kapott ortogonális bázis irányítása megegyezik az eredetivel. Ha az ortonormált $\mathbf {v} _{1},\dots ,\mathbf {v} _{n}$ vektorokból, mint oszlopokból megalkotjuk a Q mátrixot, és az eredeti $\mathbf {w} _{1},\dots ,\mathbf {w} _{n}$ vektorokból az A mátrixot, akkor van egy R háromszögmátrix, úgy, hogy A=QR, tehát egy QR-felbontáshoz jutunk.

• QR-felbontás más módszerekkel is meghatározható, így Givens-forgatásokkal vagy Householder-tükrözésekkel.

• Kézzel számoláskor egyszerűbb, ha először csak ortogonalizálunk, és csak a végén normalizálunk. Így elkerüljük a kétszeres normalizációt, és gyakran egyszerűbb értékekkel kell számolni. Kifizetődő az ortogonalizáció előtt egy Gauß-eliminációt is elvégezni.

Példa

Vegyük az

$A={\begin{bmatrix}1&2&1\end{bmatrix}}\,$

mátrix magterét mint R³ alterét és adjunk meg benne egy ortogonális bázist!

A feladatot az

$\mathbf {a} \mathbf {b} =\sum \limits _{i=1}^{3}\mathbf {a} _{i}\mathbf {b} _{i}$

sztenderd skalárszorzat szerint végezzük el!

Megoldás:

A dimenziótétel szerint a magtér kétdimenziós, ugyanis dim(R³) = dim Ker A + dim Im A, de A oszlopai skalárok, így dim Im A = 1. A kétdimenziós magtérnek kételemű a bázisa. A magtér egy alkalmas bázisa lehet az {v₁ = (2, -1, 0), v₂ = (1, 0, -1)}, mert a két vektor nyilvánvalóan lineárisan független, és mindkettő magtérbeli, mivel

${\begin{bmatrix}1&2&1\end{bmatrix}}\cdot {\begin{bmatrix}2&1\\-1&0\\0&-1\end{bmatrix}}={\begin{bmatrix}0&0\end{bmatrix}}$.

Feladatunk most már a bázisvektorok oszlopmátrixának ortogonalizálása. Alkalmazzuk az eljárást {v₁, v₂}-re!

$\mathbf {u} _{1}=\mathbf {v} _{1}={\begin{bmatrix}2\\-1\\0\end{bmatrix}}$,

$\mathrm {proj} _{\mathbf {u} _{1}}\mathbf {v} _{2}=\left\langle \mathbf {u} _{1},\mathbf {v} _{2}\right\rangle {\frac {\mathbf {u} _{1}}{\|\mathbf {u} _{1}\|^{2}}}={\frac {2\cdot 1+(-1)\cdot 0+0\cdot (-1)}{2^{2}+(-1)^{2}+0^{2}}}{\begin{bmatrix}2\\-1\\0\end{bmatrix}}={\frac {2}{5}}\cdot {\begin{bmatrix}2\\-1\\0\end{bmatrix}}={\begin{bmatrix}{\frac {4}{5}}\\-{\frac {2}{5}}\\0\end{bmatrix}}$,

$\mathbf {u} _{2}=\mathbf {v} _{2}-\mathrm {proj} _{\mathbf {u} _{1}}\mathbf {v} _{2}={\begin{bmatrix}1\\0\\-1\end{bmatrix}}-{\begin{bmatrix}{\frac {4}{5}}\\-{\frac {2}{5}}\\0\end{bmatrix}}={\begin{bmatrix}{\frac {1}{5}}\\{\frac {2}{5}}\\-1\end{bmatrix}}$.

Ellenőrizzük vektoriális szorzattal! Mivel

$\mathrm {Ker} \,A=\{(x,y,z)\in \mathbf {R} ^{3}\mid x+2y+z=0\}\,$,

ezért nincs más feladatunk, mint a

$x+2y+z=0\,$

síkban lévő két merőleges vektort mondanunk. Legyen ugyanaz az első:

$\mathbf {u} _{1}={\begin{bmatrix}2\\-1\\0\end{bmatrix}}$,

ez valóban a síkban van. Most vegyük az (1, 2, 1) normálvektor és az előbbi vektoriális szorzatát:

$\mathbf {u} _{1}={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\1&2&1\\2&-1&0\end{vmatrix}}=1\mathbf {i} +2\mathbf {j} -5\mathbf {k}$,

ami valóban párhuzamos a fent kapott vektorral, éspedig az 5-szöröse. Ebből is világosan látható, hogy az ortogonális vektorrendszer nem egyértélmű (még akkor sem, ha egységvektorokat választunk bázisnak).

Ortonormalizáció

Az algoritmus egy változata nemcsak ortogonalizál, hanem normalizál is, így a $\mathbf {w} _{1},\dots ,\mathbf {w} _{n}$ független vektorokból ortonormált rendszert kapunk, ami ugyanazt az alteret generálja, mint a kiindulási vektorok.

A $\mathbf {v} _{1},\dots ,\mathbf {v} _{n}$ vektorok ortonormált rendszert alkotnak, hogyha az ortogonalizáció után normáljuk is őket:

$\mathbf {v} _{1}={\frac {\mathbf {w} _{1}}{\left\|\mathbf {w} _{1}\right\|}}$ (az első vektor normalizációja)

$\mathbf {v} _{2}^{\prime }=\mathbf {w} _{2}-\langle \mathbf {v} _{1},\mathbf {w} _{2}\rangle \cdot \mathbf {v} _{1}$ (a második vektor ortogonalizációja)

$\mathbf {v} _{2}={\frac {\mathbf {v} _{2}^{\prime }}{\left\|\mathbf {v} _{2}^{\prime }\right\|}}$ (a második vektorból kapott $\mathbf {v} _{2}^{\prime }$ vektor normalizációja)

$\mathbf {v} _{3}^{\prime }=\mathbf {w} _{3}-\langle \mathbf {v} _{1},\mathbf {w} _{3}\rangle \cdot \mathbf {v} _{1}-\langle \mathbf {v} _{2},\mathbf {w} _{3}\rangle \cdot \mathbf {v} _{2}$ (a harmadik vektor ortogonalizációja)

$\mathbf {v} _{3}={\frac {\mathbf {v} _{3}^{\prime }}{\left\|\mathbf {v} _{3}^{\prime }\right\|}}$ (a harmadik vektorból kapott $\mathbf {v} _{3}^{\prime }$ vektor normalizációja)

$\vdots$

$\mathbf {v} _{n}^{\prime }=\mathbf {w} _{n}-\sum _{i=1}^{n-1}\langle \mathbf {v} _{i},\mathbf {w} _{n}\rangle \cdot \mathbf {v} _{i}$ (az $n$-edik vektor ortogonalizációja)

$\mathbf {v} _{n}={\frac {\mathbf {v} _{n}^{\prime }}{\left\|\mathbf {v} _{n}^{\prime }\right\|}}$ (a $\mathbf {v} _{n}={\frac {\mathbf {v} _{n}^{\prime }}{\left\|\mathbf {v} _{n}^{\prime }\right\|}}$-edik vektorból kapott $\mathbf {v} _{n}^{\prime }$ vektor normalizációja)

Másként, a $\mathbf {v} _{j}$ és a $\mathbf {v} _{j}^{\prime }$ vektorok, ahol $j=1,2,\dots ,n$, rekurzívan is definiálhatók:

$\mathbf {v} _{j}^{\prime }=\mathbf {w} _{j}-\sum _{i=1}^{j-1}\langle \mathbf {v} _{i},\mathbf {w} _{j}\rangle \cdot \mathbf {v} _{i}$ és $\mathbf {v} _{j}={\frac {\mathbf {v} _{j}^{\prime }}{\left\|\mathbf {v} _{j}^{\prime }\right\|}}$

Általában nem kapunk kitüntetett rendszert. A jobb- vagy balsodrású rendszerhez először rendezni kell a vektorokat.

Példa

$\mathbb {R} ^{2}$-ben a $\langle \cdot ,\cdot \rangle$ skalárszorzattal adva van a következő bázis:

$\mathbf {w} _{1}={\begin{pmatrix}3\\1\end{pmatrix}},\quad \mathbf {w} _{2}={\begin{pmatrix}2\\2\end{pmatrix}}$

Ezekből kiszámítunk egy $\mathbf {v} _{1}$ és $\mathbf {v} _{2}$ vektort, melyek $\mathbb {R} ^{2}$ egy ortonormált bázisát alkotják.

$\mathbf {v} _{1}={\frac {\mathbf {w} _{1}}{\left\|\mathbf {w} _{1}\right\|}}={\frac {1}{\sqrt {10}}}\cdot {\begin{pmatrix}3\\1\end{pmatrix}}$

$\mathbf {v} _{2}^{\prime }=\mathbf {w} _{2}-\langle \mathbf {v} _{1},\mathbf {w} _{2}\rangle \cdot \mathbf {v} _{1}={\begin{pmatrix}2\\2\end{pmatrix}}-{\frac {1}{\sqrt {10}}}\cdot \left\langle {\begin{pmatrix}3\\1\end{pmatrix}},{\begin{pmatrix}2\\2\end{pmatrix}}\right\rangle \cdot {\frac {1}{\sqrt {10}}}{\begin{pmatrix}3\\1\end{pmatrix}}={\frac {1}{5}}{\begin{pmatrix}-2\\6\end{pmatrix}}$

$\mathbf {v} _{2}={\frac {\mathbf {v} _{2}^{\prime }}{\left\|\mathbf {v} _{2}^{\prime }\right\|}}={\sqrt {\frac {25}{40}}}\cdot {\frac {1}{5}}{\begin{pmatrix}-2\\6\end{pmatrix}}={\frac {1}{\sqrt {10}}}\cdot {\begin{pmatrix}-1\\3\end{pmatrix}}$

Források

• Freud Róbert: Lineáris algebra (ELTE Eötvös Kiadó, 1998)
• Szörényi Miklós: Szemléletes lineáris algebra - összefoglaló I. informatikusoknak PDF (SZE MTK jegyzet, 2005)
• A kétdimenziós és háromdimenziós eset számítógépes animációval
• MIT Linear Algebra Lecture on Gram-Schmidt (angolul)
• K. Kirchgessner, M. Schreck: Vektoranalysis für Dummies. Das Pocketbuch Paperback . Wiley-VCH, 2012. ISBN 978-3-527-70742-3

Fordítás

Ez a szócikk részben vagy egészben a Gram-Schmidtsches Orthogonalisierungsverfahren című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.