Görbeillesztés (matematika)
A görbeillesztés feladata olyan függvény meghatározása, ami egy adatsor analitikus közelítése.
A függvény grafikonjaként adódó görbére nem feltétlenül illeszkednek a koordinátájú pontok, ilyenkor azt mondjuk, hogy a görbe többé vagy kevésbé jól közelíti a pontsort. Az illeszkedési kritérium különböző lehet csakúgy, mint a görbe, azaz a függvény (függvények) típusa.
A feladat egy általánosítása, amikor a síkon ábrázolható ponthalmazhoz keresünk implicit egyenlettel megadható görbét. Másik általánosítás a adatsort közelítő felület meghatározása. Rokon probléma az adott görbék, görbeívek egyszerűbb görbékkel való helyettesítése.
Alkalmazási területek
[szerkesztés]Egy természeti, gazdasági, társadalmi stb. folyamat lefolyását modellező matematikai formula kísérleti meghatározásához méréseket kell végezni. A mérések adatai egyrészt hibákkal terheltek (szóródás), másrészt bizonyos tartományok kimaradhatnak az adatgyűjtésből. Az adatsor ) számpárjait derékszögű, illetve a problémának jobban megfelelő affin vagy poláris koordináta-rendszerben ábrázolva egy görbe pontjaira emlékeztető pontsort vagy egy pontfelhőt kapunk.
Empirikus formulák
[szerkesztés]A görbeillesztés egyik célja, hogy a meghatározott függvény (és esetleg az inverz függvény (formula) ismeretében a vizsgált folyamat összetartozó értékpárjait kiszámíthassuk. A másik cél az lehet, hogy a kiválasztott függvény együtthatóit meghatározzuk (például a szabadesés egyenletében számértékére kapunk kísérleti becslést).
Illesztési típusok
[szerkesztés]Interpoláció
[szerkesztés]Olyan görbét kell keresni, ami minden adatponton áthalad. A „szabálytalan” pontsorhoz szinte sohasem illeszthető egyszerű egyenlettel leírható függvény/grafikon.
Lineáris interpoláció
[szerkesztés]Az intervallumokhoz egyenletű egyenes szakaszokat illesztünk. Ezek egyenként helyettesítik a folyamatot leíró grafikon íveit. A formulák a két ponton átmenő egyenes egyenletével kaphatók:
Parabolikus interpoláció
[szerkesztés]Több, egymáshoz csatlakozó intervallum feletti görbeívet egy polinom grafikonjával helyettesítjük. A megfelelő együtthatók meghatározásához két formula ismert:
- Lagrange-féle interpolációs formula:
- ahol az függvények a Lagrange-féle interpolációs polinomok:
- Newton-féle interpolációs formula:
- ahol az kifejezések a Newton-féle interpolációs együtthatók:
A formula és ezzel a számolás egyszerűbb, ha az intervallumok egyenlőek. Főleg tabellált függvényeknél (függvénytáblázatoknál) használják (használták) a táblázatban nem szereplő közbenső értékek számítására. A feladat gyakorlati fontosságát jelzi, hogy több neves matematikus adott meg erre interpolációs formulát: Newton, Bessel, Stirling.
Regresszió
[szerkesztés]Mindkét modell esetében alkalmazható eljárás az, ha lemondunk az empirikus formulával adódó függvénygörbe és a mérési adatokat reprezentáló pontok illeszkedéséről, csupán azt követeljük meg, hogy az mérési helyeken a mért és a számított értékek eltérése minimális legyen. Az eltérés mértékét többféleképpen írhatjuk elő:
- 1 - Az abszolút hibák összege legyen minimális.
- 2 - A hibák négyzetének összege legyen minimális.
Az első feltételnek eleget tevő egyenletes közelítés meghatározására nincsenek általános módszerek. A négyzetes hibákat minimáló közelítés meghatározására a Gauss nevéhez kötött, a legkisebb négyzetek módszere nevű algoritmust használják.
Lineáris regresszió
[szerkesztés]A matematikai statisztika leggyakrabban alkalmazott modellje. Több típusát a legtöbb táblázatkezelő és matematikai szoftver megvalósítja (Excel, Maple V, Matlab stb):
- 1- Egyszerű kétváltozós regresszió az elsőfokú függvény együtthatóinak meghatározására szolgál.
- 2- Inverz regresszió az inverz relációval illesztett összefüggés a négyzetes hibaösszeget minimalizálja.
- 3- Többváltozós lineáris regresszió az összetartozó mérési adatokhoz az összefüggésüket leíró elsőfokú függvényt határozza meg.
Linearizáló módszer
[szerkesztés]A mérési adatokat ábrázoló pontdiagramról látható, hogy egyenes helyett inkább valamilyen, a vizsgált jelenség tulajdonságaiból is következtethető görbe illik a modellhez. A legkisebb négyzetek módszere ekkor is alkalmazható, de a számolás ilyenkor a formula jellegéből fakadóan nehézkesebb. A linearizáló módszer abból áll, hogy az eredeti változók helyett, velük összefüggő, de egymással lineáris kapcsolatban lévő változókat vezetünk be.
- Például az empirikus formulából az helyettesítésekkel az lineáris kapcsolat adódik. Ennek együtthatóit meghatározva az eredeti formula konstansai adódnak: .
Középértékek módszere
[szerkesztés]A linearizáló módszer esetenként nem eléggé pontos. Javítható a becslés, ha az adathalmazt két vagy több részre osztjuk és mindre elvégezzük a számítást. Az egyes paraméterek számított értékeinek számtani (vagy súlyozott) közepét képezzük.
Spline (szplájn) approximáció
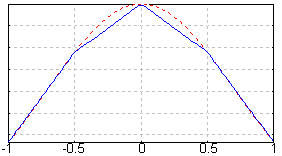
[szerkesztés]Az adatsort szakaszonként közelítő görbeívek érintője a csatlakozási pontokban közös. Az érintőkben a nyelvtani többes azt jelenti, hogy a csatlakozó görbéknek az adott pontban közös lehet az elsőrendű (egyenes), a másodrendű (simulókör) stb. érintője. Minél magasabb rendben érintkeznek, annál simább a spline, annál tökéletesebb illesztés. A spline approximációt nem csak adatsorok közelítésére, hanem komplikált, nehezen kezelhető egyenletű görbék helyettesítésére használják. (L.: Kosárgörbe, klotoid, átmeneti ív.) A számítógépes grafikában a szabálytalan vonalakat Bèzier-spline-ok alkalmazásával digitalizálják. (Az alábbi példában a lineáris spline-t (kék vonal) az adatokhoz (piros pontok) illesztjük.)
További elérhető illusztrációk:
- Harmadfokú spline approximáció JSXGraph médián
- Előadások a spline interpolációról
- Harmadfokú spline interpoláció, előadási jegyzet PDF
Irodalom
[szerkesztés]- Bartsch, Hans-Jochen: Matematische formeln (Veb Fachbuchverlag, Leipzig, 1967) (németül)
- Bronstein – Szemengyajev: Matematikai zsebkönyv (Műszaki, 1987) ISBN 963 1053091
- Hack F. & all.: Négyjegyű függvénytáblázatok etc. (Nemzeti Tankönyvkiadó, 2004) ISBN 978-963-19-5703-7
- Reinhardt – Soeder: SH Atlasz – Matematika (Springer-Verlag, 1993)
További információk
[szerkesztés]- Letölthető interaktív Flash szimuláció a görbeillesztésről – polinommal illusztrálva, magyarul. Elérés: