Whitney-esernyő

A felület egy része

A matematikában a Whitney-esernyő (vagy Whitney esernyője, esetleg Cayley-esernyő) egy önmagát metsző, háromdimenziós felület. Nevét Hassler Whitney amerikai matematikusról kapta. Azok az egyenesek alkotják, amik egy adott parabolán, tehát a vezérgörbén keresztülmennek, egy adott vezéregyenesre merőlegesek, a parabola tengelyével párhuzamosak és annak merőleges felező síkján, az iránysíkon fekszenek.

Képletek

A Whitney-esernyő megadható Descartes-féle koordináta-rendszerben paraméteres egyenletrendszer segítségével:

$x(u,v)=uv$; $y(u,v)=u$; $z(u,v)=v^{2}$, ahol az u és v valós számok. Megadható implicit módon is:

$x^{2}=y^{2}z$.

Ez a képlet tartalmazza a negatív z tengelyt is (amit az esernyő „fogantyújának” is neveznek).

Tulajdonságai

Whitney-féle esernyő mint egyenes mozgása által létrejövő vonalfelület.

Whitney-esernyő egyetlen szálból elkészítve egy műanyag kockában

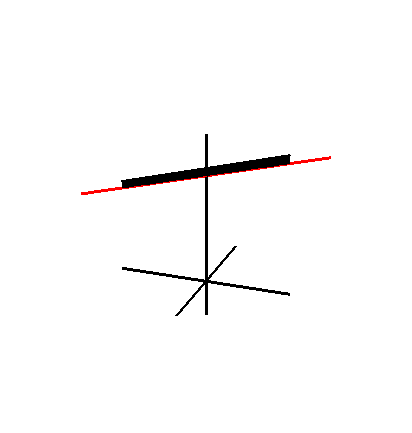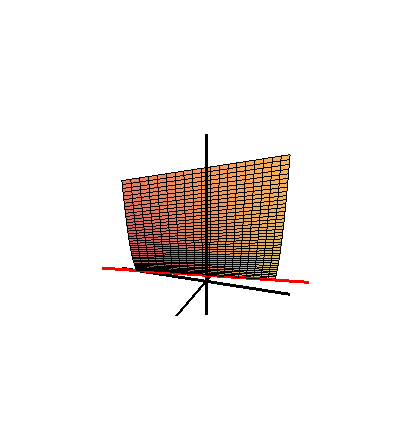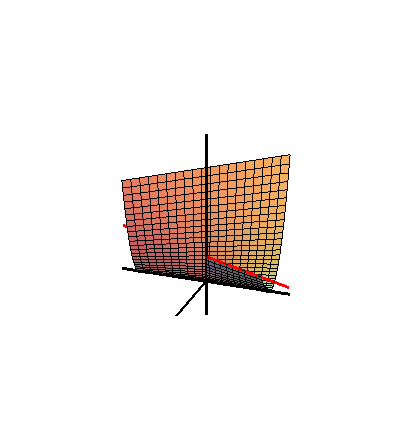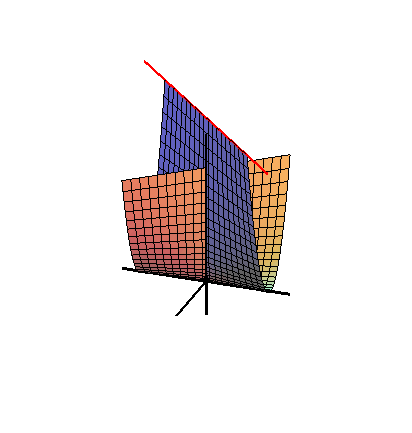
A Whitney-féle esernyő egy parabolakonoid vonalfelület. Fontos szerepet játszik a szingularitáselméletben, a becsípődésesi szingularitás egyszerű lokális modelljeként. A húrelméletben a Whitney-brane egy D7-brane wrapping, aminek a szingularitásait lokálisan a Whitney-esernyő modellezi. A Whitney-esernyők az F-elmélet Sen-féle gyenge csatolási határainál is előjönnek.

Kapcsolódó szócikkek

• Esernyő
• Keresztsapka
• Konoid
• Vonalfelület

Jegyzetek

• Whitney's Umbrella. The Topological Zoo. The Geometry Center. [2012. május 23-i dátummal az eredetiből archiválva]. (Hozzáférés: 2006. március 8.) (Képek és videók a Whitney-esernyőről)