| Leírás |
Ábra |
Tehetetlenségi nyomaték |
Megjegyzés
|
Vékony hengerpalást nyitott végekkel  sugárral és sugárral és  tömeggel tömeggel
|
 |
 |
Ennél a képletnél feltételezzük, hogy a palást vastagsága elhanyagolható. A következő test speciális esete  -re. -re.
|
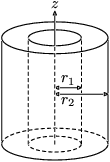
Vastag hengergyűrű nyitott végekkel, belső sugár  , külső sugár , külső sugár  , hossz , hossz  és tömeg és tömeg 
|
|

![{\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{1}}^{2}+{r_{2}}^{2}\right)+h^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e48edde3cc6fa2d6c3d6c4bbc9bf9b370269606)
vagy ha bevezetjük a  = =  normalizált vastagságot és normalizált vastagságot és  , ,
akkor 
|
–
|
Tömör henger  sugárral, sugárral,  magassággal és magassággal és  tömeggel. tömeggel.
|
 |

 |
Ez az előző test speciális esete  -ra. -ra.
|
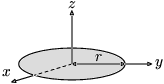
Vékony tömör tárcsa  sugárral és sugárral és  tömeggel. tömeggel.
|
 |

 |
Ez az előző test speciális esete  -ra. -ra.
|
Tömör gömb  sugárral és sugárral és  tömeggel. tömeggel.
|
 |
 |
–
|
Gömbhéj  sugárral és sugárral és  tömeggel tömeggel |
 |
 |
–
|
Egyenes körkúp  sugárral, sugárral,  magassággal és magassággal és  tömeggel tömeggel
|

|

 |
–
|
Tömör téglatest  magassággal, magassággal,  szélességgel, szélességgel,  hosszúsággal, és hosszúsággal, és  tömeggel tömeggel |
 |


 |
Hasonlóan tájolt kocka  élhoszal: élhoszal:  . .
|
Rúd  hosszal és hosszal és  tömeggel tömeggel |
 |
 |
Ez a képlet feltételezi, hogy a rúd végtelenül vékony (de merev) huzal. Ez speciális esete az előző testnek  és és  esetén. esetén.
|
Rúd  hosszal és hosszal és  tömeggel tömeggel |
 |
 |
Ez a képlet feltételezi, hogy a rúd végtelenül vékony (de merev) huzal.
|
Tórusz  középátmérővel, középátmérővel,  rúdátmérővel és rúdátmérővel és  tömeggel. tömeggel. |
 |
Az átmérőre: 
A függőleges tengelyre:  |
–
|
Vékony tömör sokszög alakú lemez  , ,  , ,  , …, , …,  csúcspontokkal és csúcspontokkal és  tömeggel. tömeggel. |
 |
 |
–
|





















![{\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{1}}^{2}+{r_{2}}^{2}\right)+h^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e48edde3cc6fa2d6c3d6c4bbc9bf9b370269606)

































