Szerkesztő:Alfa-ketosav/Komag

A matematikában egy f : X → Y morfizmus komagja olyan Q objektum és egy q : Y → Q morfizmus, ahol a $q\circ f$ összetett morfizmus a zéró morfizmus, és ahol Q egy bizonyos értelemben a „nagyobb” objektum ezzel a tulajdonsággal. Gyakran q-t értik ez alatt, és Q-t hasonlóképp f komagjának nevezik.

A komagok a kategóriák magjainak duálisai, innen kapják a nevüket.

Az általános algebra számos területén, így az Abel-csoportoknál, a vektortereknél vagy a moduloknál, egy f : X → Y homomorfizmus komagja Y f képével vett hányadosa, vagyis $\mathrm {coker} f=Y/\mathrm {im} (f)$. A topológiában például egy Hilbert-terek közti korlátos operátor esetén a kép lezártját kell venni a hányadosszámítás előtt.

Definíció

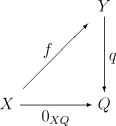
A komagot az Abel-kategóriák körében definiálják, ahol értelmezhető a zéró morfizmus. A f : X → Y morfizmus komagja az f és a 0_XY : X → Y koekvalizátoraként definiálható. Ez azt jelenti, hogy f : X → Y komagja az a Q objektum, amit egy q : Y → Q morfizmussal kaptunk meg, ami az alábbi

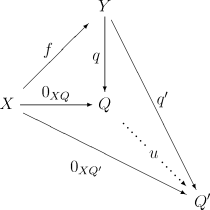
diagram szerint kommutatív. Ezenkívül a q morfizmusnak univerzálisnak kell lennie a diagram szerint, ami azt jelenti, hogy nincs másik egyedi u : Q → Q-val rendelkező egyedi q-ból megkapható q′: Y → Q′ morfizmus:

Mint minden koekvalizátor, a q : Y → Q komag szükségszerűen epimorfizmus. Fordítva, egy epimorfizmus konormális, ha egy morfizmus komagja. Egy kategória konormális, ha minden epimorfizmusa konormális.

Fordítás

Ez a szócikk részben vagy egészben a Conoyau című francia Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Források

• Saunders Mac Lane. Categories for the Working Mathematician, második, 64. o. (1978)