Spidron

A spidron egy Erdély Dániel grafikus által felismert és matematikailag is leírt geometriai alakzat, amelyet Erdély hálós szerkezete és spirális jellege miatt az angol spider (magyarul: pók) és a geometriai alakzatok görög szóvégéből (dron) alkotott szóösszetétellel nevezett el.

Rubik Ernő által szignált modell

A spidron Erdély Dániel önálló munkája, amelyet az 1979–1980-as tanévben Rubik Ernő által kiadott házi feladat megoldásaként készített el a Magyar Iparművészeti Főiskola (a mai MOME) formatan órájára. Síkbeli kísérletekkel korábban is próbálkozott még a Nyomdaipari Szakmunkásképző Intézetben, de a térben mozgatható, harmonikaszerű változatot akkor hozta létre, amelyre Rubik csak ennyit mondott: „Ilyet még nem láttam!”. Ez a meglepetést mutató megjegyzés adta meg a kezdő lökést a további fejlesztésekhez és munkához.

A spidron leírása és a spidron-rendszer

A spidron geometriai alakzata

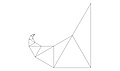
A spidron egy véges területű, de végtelen oldalú sík poligon, amely középpontosan szimmetrikus és négy logaritmikus spirál pontjaira helyezhető csúcsai vannak. Kétféle háromszög mértani sorozat szerint kisebbedő (avagy ellenkező irányból tekintve, növekvő) oldalainak összeillesztésével, avagy egy szabályos hatszög felbontásával is előállítható.

Jól megjegyezhető, emblematikus formája miatt adta Erdély ennek az alakzatnak a „spidron” nevet, amelyet védjegyeztetett is, illetve az egész rendszert is erről nevezte el.

Klasszikus esetben a kétféle háromszög szögei rendre 60°, 60°, 60° és 30°, 120°, 30°-osak, számtalan másféle változat is előállítható más és más háromszögpárból. Az összes megoldás rendszert alkot és rendkívüli síkbeli, térbeli, sőt, különböző összetételekben sík és térkitöltő rendszerekké, dinamikus, mozgatható szerkezetekké állíthatók össze.

Érdemes első megközelítésben az úgynevezett „klasszikus” (szabályos hatszög alakú) spidront tárgyalni, amely során olyan fogalmak kerülhetnek bevezetésre, amelyek a továbbiakban a meghatározások szerint alkalmazhatók.

Semi-spidron, azaz félspidron

Ez az alakzat, amelyből – a leghosszabb éleket összeillesztve – két darabból egy spidron adódik. A leghosszabb élre emelt egyenlőoldalú háromszög területe megegyezik egy semi-spidron területével, abba átdarabolható.

Spidron-gyűrű

Egy szabályos síkbeli hatszögbe írható hat semi-spidron kétféle szomszédos háromszögeit tartalmazó gyűrűalakú zóna. Ilyenből végtelen, egymásba ágyazható darab van. Területe mindig 3-szorosa illetve 1/3-a szomszédos gyűrűjének.

Spidron-fészek vagy spidron-tányér

Több, akár végtelen, egymásba ágyazott spidron-gyűrű sík, avagy térbeli együttese. A spidron-fészek térben mozgatható, változása megfigyelhető.

Egy érdekesség, hogy, bár az egymásba ágyazott gyűrűk sorát valóban a végtelenségig építhetjük, mégis marad egy apró lyuk a közepén, míg, ha valóban semi-spidronokból állítunk össze spidron-tányért, az zárt is lehet. Ilyenkor a semi-spidron végtelen sok oldala biztosítja ezt.

A spidron-csapat megvizsgálta a térben gömbszimmetrikusan bemozgatott spidron-tányért is, és – mivel az alkotó háromszögek kimozdulása (elfordulása) az alapsíkhoz képest az alakzat közepe felé radikálisan csökken – arra jutott, hogy kellően vékony anyag használata esetén a fizikailag megvalósított változat is lehet folyamatos, lyuk nélküli.

Az egész probléma fel sem merül, ha a spidron-fészket egy síkbeli szabályos hatszög megfelelően kiválasztott élei mentén történő hajtogatásból származtatjuk.

Hornflake

Két semi-spidron tükörszimmetrikus együttese, amikor a leghosszabb élek mentén illesztjük azokat össze.

Spidron-alapsík

Az a síkbeli alapállapot, amelyből a spidronalakú, spirális törések mentén létrejönnek a reliefek és további térbeli alakzatok. Jellemző tulajdonsága a spidron-deformációknak, hogy a fészkek középpontjai és a spidron-gyűrűk külső és belső éleinek felezőpontjai az alapsíkban maradnak.

Spidron-deformáció

A spidron-háló mentén történő nyúlásmentes és szimmetriáját megtartó deformációk a legkülönfélébb relief-szerű és térbeli alakzatok megvalósítását is lehetővé teszik. A deformációk során az alakzatokat felépítő háromszögek mindvégig merevek maradnak.

Spidronizálás

Kialakult metódus számos ismert térbeli test síkoldalainak spidron-felületekkel való helyettesítésére. Így született több újfajta térkitöltő modul, térrács és mozgatható felület.

Spidron-formula

Illusztráció a spidron-képlethez.
α a spidron-fészek legkülső gyűrűjének kerületén található élek dőlésszöge az alapsíkhoz képest.
α₂ ugyanezen gyűrű belső éleinek dőlésszöge (amely élek egyúttal az eggyel bentebbi gyűrű külső élei). A képlet ezen belső élsor dőlésszögét adja meg a külső függvényében.

Sok év munkájával, több hazai matematikus egybehangzó levezetése révén megszületett a végső spidron-képlet, amely lehetővé teszi a számítógépes modellezést is.

$\alpha _{2}=\arcsin \left({\sqrt {-1+4\cos(\alpha )-3\cos ^{2}(\alpha )}}\right)$

A dolog nehézségét többek között az adta, hogy az egyes gyűrűket alkotó háromszögek alapsíkkal bezárt szögéből a többi gyűrű hasonló szögei csupán rekurzióval adódnak. A megoldást Erdély Dániel társszerzősége mellett Kiss Gergő mutatta be The Derivation of the Spidron Formula címmel a 2018. évi Gathering for Gardner (G4G13) konferencián az egyesült államokbeli Atlantában.

A spidron-geometria és deformáció tanulságai nyomán született az íves, görbült, de szintén torzulásmentes "SpHidron gyűrődés" leírása, amelyet Erdély 2011-ben mutatott be és publikált a portugál Coimbrában megrendezett Bridges Art Math & Music konferencián.

Spidron-rebegés

Egy különösen érdekes tulajdonsága a spidron-deformációnak, hogy egy spidron-tányér külső éleit az alapsíkhoz képest egyenletesen elforgatva a következő gyűrű külső élsora (amely a külső gyűrű belső élsorával egybeesik), egy ideig – ugyan egyre lassuló módon – egy irányba forog a külső élek forgásirányával, de egy jellegzetes ponton – amikor a szomszédos élek egymással éppen derékszöget zárnak be – megáll és a végállapotig ellenkező irányban forog. Ez az egész spidron-tányérnak egy rebegő jelleget kölcsönöz, mivel a kisebb gyűrűk ezt a megfordulást enyhébb kitérésekkel, de követik. Mindennek következménye az is, hogy a spidron-deformáció formulájának bizonyos határok között dupla mennyiségű gyöke van.

Spidronok a nemeuklideszi geometriákban

A témával dr. Molnár Emil foglalkozott és megállapította, hogy a Bolyai-Lobacsevszkij-féle hiperbolikus geometria is alkalmas spidronizált minták alkotására. Craig S. Kaplan pedig a hiperbolikus spidron-csempézésekhez írt programot, amelynek eredményeként néhány mintázatot publikált honlapján. Ezeket az azóta elhunyt Marc Pelletier – a spidron-csapat oszlopos tagjának – felkérésére készítette.

Alkalmazási lehetőségek

Köztéri alkotások, plasztikák és installációk

• 
  SH – Térkitöltő spidron-plasztika – 2005, falemez és 3D-print, 160 x 160 x 160 cm., Wijk en Aalburg, Hollandia. (Magántulajdonban: Walt van Ballegooijen. Kivitelező: Sági István asztalosmester.
• 
  Spidron-relief – 2006, falemez és 3D-print, 530 x 200 cm., Országos Orvosi Rehabilitációs Intézet, Budapest, igazgatósági épület. (Belsőépítész: Szenes István DLA. Kivitelező: Sági István asztalosmester.)
• 
  Mennyezeti dekoráció, aranyra festett műanyag, fémvázon. A Steigenberger lánc bécsi Herrendorf szállodájának halljában. (Kivitelező: Sági István asztalosmester.)
• 
  Spidron-félkocka – 2005, festett fa fémvázon. Kb. 420 x 300 cm. Gyulakeszi, Csigó malom. (Eredetileg a Jövő házának előcsarnokában volt tükörborítással, felújításkor került lefestésre. Kivitelező: Sági István asztalosmester)

További alkalmazások és lehetőségek

A spidron, mint forma, mint deformáció és mint rendszer, megjelenése óta számos ötlet, alkalmazás és geometrián túlmutató jelenség modelljeként is kipróbálásra került^[forrás?]. Jellegzetes területe eddig főleg a design, a belsőépítészet és az oktatás területén mutatkozott.^[forrás?]

Spidron-workshopok, előadások és kiállítások tucatjait tartotta Erdély a világ minden táján és az interneten Kanadától Kínáig^[forrás?]. A bemutatók nagy részében a már ismert geometriai és mérnöki megoldások kiegészítéseként és változataiként jelent meg, de számos újításnak is formanyelvévé vált.^[forrás?]

Így, a magától értetődő ajándéktárgyakon és design alkotásokon túl, egyedi termékek prototípusai is készültek spidronból: pl.: parketta, tapéta- és csempeváltozatok, reliefek és támfalak változatai^[forrás?].

Kiemelkedő érdeklődés övezte^[forrás?] a spidronból készíthető energetikai, akusztikai és szórakoztató elektronikai megoldásokat is, amelyek kifejlesztés alatt állnak, ezért még nem publikusak^[forrás?].

Anyagszerkezeti, nanotechnológiai, grafén-modellek tervezése épp úgy munka alatt vannak^[forrás?], mint űrépítészeti, biztonsági és szűrőrendszerek tervei^[forrás?]. Említésre érdemes területek még a fizikai és társadalmi folyamatok spidronalapú modellezésére alkalmas elméletek^[forrás?]. A közeljövőben várható^[forrás?] több fejlesztés közzététele különböző ipari és termékbemutatókon valamint – a tervek szerint – 2025-ben a Kyoto-i World EXPO-n^[forrás?].

Az elnevezés jogi védelme

A spidron név alatt több, szerzői jogi védelem alatt is álló alkotás van, s bár maga a „Spidron” szó is védelem alatt áll, annak csak magyar területi érvényessége és jó hangzása miatt azt újabban mások is használják, mint például híradástechnikában a spidron-antenna, vagy az audio-technikai alkalmazás.

Használati mintaoltalom védi a két éve kidolgozott, a földrengés káros hatásait csökkentő, spidronalapú, ún. SBRICK építőelemet.

Galéria

• 
  Semi-spidron
• 
  Spidron-gyűrű
• 
  Spidron-fészek
• 
  A hornflake