|
|
Ez a szócikk vagy szakasz lektorálásra, tartalmi javításokra szorul. A felmerült kifogásokat a szócikk vitalapja részletezi (vagy extrém esetben a szócikk szövegében elhelyezett, kikommentelt szövegrészek). Ha nincs indoklás a vitalapon (vagy szerkesztési módban a szövegközben), bátran távolítsd el a sablont!
Csak akkor tedd a lap tetejére ezt a sablont, ha az egész cikk megszövegezése hibás. Ha nem, az adott szakaszba tedd, így segítve a lektorok munkáját! |
A Runge–Kutta-módszerek családja a differenciálegyenletek numerikus analízisének széles körben ismert és alkalmazott közelítő eljárása, amelyet Carl Runge és Martin Kutta német matematikusok dolgoztak ki 1900 körül.
A közönséges negyedrendű Runge–Kutta-módszer
[szerkesztés]A Runge–Kutta-módszercsalád közönséges negyedrendű tagja annyira elterjedten használatos, hogy egyszerűen csak „a Runge–Kutta-módszer”-ként hivatkoznak rá. E módszer az alábbi kezdetiérték-probléma egy negyedrendű közelítő megoldását adja.

Azaz tetszőlegesen rögzített pozitív valós, tipikus esetben kicsiny  lépésköz esetén az
lépésköz esetén az  -edik lépésben a kezdetiérték-probléma
-edik lépésben a kezdetiérték-probléma  megoldásának egy olyan
megoldásának egy olyan

közelítését adja a

helyen, amely közelítés hibája negyedrendű. E negyedrendűség azt jelenti, hogy a választott lépésköz zsugorításakor annak negyedik hatványával zsugorodik a hibára adott felső becslés. Például a lépésköz harmadolása árán, azaz nagyjából háromszor annyi számolás árán a hibakorlát  -szeresre zsugorodik.
-szeresre zsugorodik.
A  lépésköz rögzítése után az alábbi,
lépésköz rögzítése után az alábbi,  -szerinti rekurziós lépésekkel kapjuk az
-szerinti rekurziós lépésekkel kapjuk az  megoldásfüggvény közelítését.
megoldásfüggvény közelítését.

Így, a  helyhez tartozó
helyhez tartozó  közelítőérték egyenlő a
közelítőérték egyenlő a  helyhez tartozó
helyhez tartozó  közelítőérték, plusz a becsült meredekség szorozva az intervallum
közelítőérték, plusz a becsült meredekség szorozva az intervallum  hosszával. A meredekség becslése egy, most nem részletezett matematikai megfontolás alapján súlyozott középértéke az alábbi négy meredekségi becslésnek:
hosszával. A meredekség becslése egy, most nem részletezett matematikai megfontolás alapján súlyozott középértéke az alábbi négy meredekségi becslésnek:

E négy közelítés átlagolásánál a  és
és  szélekhez képest a
szélekhez képest a  felezőnél dupla súlyt alkalmazunk.
felezőnél dupla súlyt alkalmazunk.

Mivel a megoldásfüggvény felvett értékeire csak additív műveleteket és a skalárral való szorzás műveletét alkalmazzuk, lényegében ezért a módszer nem csak skalár értékű megoldásfüggvények, hanem vektor értékűek esetén is alkalmazható. Ilyen például a Schrödinger-differenciálegyenlet, amelynek Hamilton-operátorát használjuk a fenti szerepében.
A fent említett Runge–Kutta-módszercsalád általánosítása az explicit Runge–Kutta-módszer, amit a

ad meg, ahol





- (Megjegyzés: a fenti egyenletek különböző formákban is megjelenhetnek egyéb forrásokból, de jelentésük azonos).
Ahhoz hogy meghatározzunk egy bizonyos módszert,kell egy s egész változó (a szakaszok száma), illetve az aij (1 ≤ j < i ≤ s), bi (i = 1, 2, ..., s) és a ci (i = 2, 3, ..., s) együtthatók. Ezek az adatok általában egy mnemonik eszközbe kerülnek be, ami a Butcher táblájaként ismert (Butcher tableau, John C. Butcher neve után):
|
0
|
|
 |

|
|
 |
 |

|
|
 |
 |
|

|
|

|

|

|

|
 |
|
|
|
 |
 |
 |
 |

|
A Runge–Kutta-módszer konzisztens, ha

Ugyanakkor vannak más követelmények, ha azt szeretnénk, hogy a módszernek legyen p fokszáma, így a kerekítési hiba O(hp+1) lesz. Például egy kétlépcsős módszer másodrendű ha b1 + b2 = 1, b2c2 = 1/2, és b2a21 = 1/2.
A RK4 szerkezete a következő táblázat szerint értelmezhető:
|
0
|
|
1/2 |
1/2
|
|
1/2 |
0 |
1/2
|
|
1 |
0
|
0 |
1
|
|
|
|
1/6 |
1/3 |
1/3 |
1/6
|
Habár a legegyszerűbb Runga-Kutta-módszer az Euler-módszer maga, amelynek  képlet ad meg.
Ez az egyetlen explicit Runge–Kutta-módszer egy lépcsővel.
képlet ad meg.
Ez az egyetlen explicit Runge–Kutta-módszer egy lépcsővel.
Egy példa a másodrendű két lépcsős módszerre a középponti módszer:

Az erre megfelelő táblázat:
Megjegyzendő, a középponti módszer nem a legmegfelelőbb RK-módszer. A Heun-módszer egy alternatív megoldást kínál, ahol a tábla 1/2-ei 1-re cserélődnek, és a b sora pedig [1/2,1/2].
Ha valaki minimalizálni akarja a kerekítés által keletkezett hibákat, akkor az alábbi módszert kell használnia (Atkinson p. 423). Más fontos módszerek: Fehlberg, Cash-Karp és Dormand-Prince.
A következő egy példa a kétlépcsős explicit Runge–Kutta-módszerre:
a kezdeti értéket meghatározó képlet
![{\displaystyle y'=\tan(y)+1,\quad y(1)=1,\ t\in [1,1.1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67960f717992d40a86b329a9428590e7816cb09)
a h=0,025 lépésköz
A fenti táblát meghatározó egyenrangú számítások:



 |
|
|
|

|

|
|
 |
 |

|
|

|

|
|
 |
 |

|
|

|

|
|
 |
 |

|
|

|

|
|
 |
 |

|
|

|
Az aláhúzott kifejezések jelzik a számszerû megoldásokat.Megjegyzendõ, az  s újraszámolása érdekében
s újraszámolása érdekében  -et használtunk.
-et használtunk.
Az adaptív módszer arra volt tervezve, hogy megadja a becsült helyi kerekítési hibát minden egyes RK lépésben. Ezt úgy valósította meg, hogy két módszert tartalmaz a táblázat, egyet p-ed rendűvel és egyet p-1-ed rendűvel.
A kisebb rendű lépés adott:

ahol, a  megegyezik a magasabb rendű módszerrel. Ekkor a hiba:
megegyezik a magasabb rendű módszerrel. Ekkor a hiba:

ami  . A Butcher-táblázat erre a módszerre ki van bővítve, így megadja a
. A Butcher-táblázat erre a módszerre ki van bővítve, így megadja a  értékeit:
értékeit:
|
0
|
|
 |

|
|
 |
 |

|
|
 |
 |
|

|
|

|

|

|

|
 |
|
|
|
 |
 |
 |
 |

|
|
|
 |
 |
 |
 |

|
A RK Fehlberg módszernek a két rendszere az ötöd- és negyedrendű. Ennek a kibővített Butcher-táblázata a következő:
|
0
|
|
1/4 |
1/4
|
|
3/8 |
3/32 |
9/32
|
|
12/13 |
1932/2197 |
−7200/2197 |
7296/2197
|
|
1 |
439/216 |
−8 |
3680/513 |
-845/4104
|
|
1/2 |
−8/27 |
2 |
−3544/2565 |
1859/4104 |
−11/40 |
|
|
|
16/135 |
0 |
6656/12825 |
28561/56430 |
−9/50 |
2/55
|
|
|
25/216 |
0 |
1408/2565 |
2197/4104 |
−1/5 |
0
|
Habár a legegyszerűbb adaptív Runge–Kutta-módszer a másodrendű Heun-módszert és az elsőrendű Euler-módszert foglalja magába. Ennek a kibővített Butcher-táblázata:
A hiba eredményét a lépték határozza meg.
Más adaptiv Runge–Kutta-módszerek a Bogacki-Shampine-módszer (harmad-és másodrendű), a Cash-Karp-módszer és a Dormand-Prince-módszer (mindkettő ötöd- és negyedrendű).
Az implicit módszerek jóval általánosabbak az expliciteknél. Az eltérés a Butcher-táblázatnál merül fel: az implicit módszernél, a mátrix aij együtthatója nem feltétlenül alacsony háromszög:

A megközelítő megoldás a kezdeti érték problémára utal az együtthatók nagyobb számára.


Az  mátrix telítettsége miatt, az egyes
mátrix telítettsége miatt, az egyes  becslése jelentékeny mértékben fog függeni az
becslése jelentékeny mértékben fog függeni az  függvénytől. A nehézségek ellenére, az implicit módszerek nagy jelentőséggel birnak az erősen stabil állapotuk miatt, ami különösen fontos a parciális differenciál egyenletek megoldásában. A legegyszerűbb példa egy implicit Runge–Kutta-módszerre fordított Euler-módszer:
függvénytől. A nehézségek ellenére, az implicit módszerek nagy jelentőséggel birnak az erősen stabil állapotuk miatt, ami különösen fontos a parciális differenciál egyenletek megoldásában. A legegyszerűbb példa egy implicit Runge–Kutta-módszerre fordított Euler-módszer:

Ennek táblázata egyszerű:

Még az egyszerűbb implicit módszer alkalmazása is bonyolulttá válhat, ami a ki kifejezésből látszik is:

Ebben az esetben, a fenti bonyolult kifejezés leegyszerűsíthető a következőképpen:

így hát

amiből következik, hogy:

Noha egyszerűbb, mint a módosítások előtti „nyers” kifejezés, ez egy implicit összefüggés, tehát a konkrét megoldás problémafüggő. A többlépéses implicit módszert sikeresen használják a kutatók. Az egyensúly összeállítása (kombinációja), a magasabb rendpontosság kevesebb lépésben és a léphetőség (stepping) egyedül az előző értékben válik érdekessé, ugyanakkor a bonyolult példa jellegzetes kivitelezése, és a tény, hogy ki ismételt megközelítései mutatják hogy ezek hasonlóak (ugyanazok).
Legyen mondjuk a  differenciálegyenlet, aminek a megoldása:
differenciálegyenlet, aminek a megoldása:
import math
import numpy as np
import matplotlib.pyplot as plt
x0=0
y0=3
h=0.8
def ypontos():
x=np.linspace(0,10,100)
y=3*np.exp(-2*x)
plt.plot(x,y,"-b")
def f(x, y):
return(-2*y)
def RungeKutta2nd(f, h, x0, y0):
x=np.arange(0, 10, h)
y=x*0
y[0]=y0
for i in range(10):
k1=h*f(x[i],y[i])
k2=h*f(x[i]+h/2,y[i]+k1/2)
y[i+1]=y[i]+k2
plt.plot(x,y, "--r")
plt.text(-0.5, 3,'Masodrendu Runge-Kutta (h=0.8)',color='red', fontsize=10)
def RungeKutta4th(f, h, x0, y0):
x=np.arange(0, 10, h)
y=x*0
y[0]=y0
for i in range(10):
k1=h*f(x[i],y[i])
k2=h*f(x[i]+h/2,y[i]+k1/2)
k3=h*f(x[i]+h/2,y[i]+k2/2)
k4=h*f(x[i]+h,y[i]+k3)
y[i+1]=y[i]+(k1+2*k2+2*k3+k4)/6
plt.plot(x,y, "--g")
plt.text(5, 3,'Negyedrendu Runge-Kutta (h=0.8)',color='green', fontsize=10)
ypontos()
RungeKutta2nd(f, h, x0, y0)
RungeKutta4th(f, h, x0, y0)
plt.show()
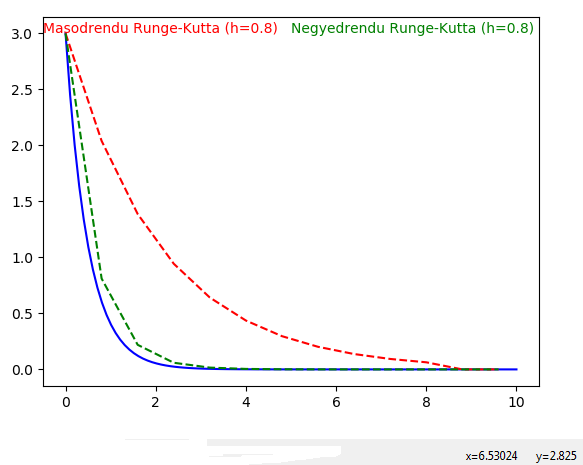
A program lefuttatása után egy grafikonon összehasonlíthatjuk a másodrendű illetve 4.-edrendű Runge-Kutta módszereket illetve a tényleges megoldást.









































![{\displaystyle y'=\tan(y)+1,\quad y(1)=1,\ t\in [1,1.1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67960f717992d40a86b329a9428590e7816cb09)















































