Homogén koordináták
Az olyan koordináta-rendszereket nevezik homogénnek, amelyekben a pontot azonosító rendezett pár (hármas, négyes stb.) elemeit egy nullától különböző számmal megszorozva ugyanazt a pontot azonosító párt (hármast, négyest…) kapjuk.
A homogén koordináták igazi jelentőségét az adja, hogy használatukkal az ideális térelemek (pont, egyenes, sík) is megadhatók.
Fontosabb típusok
[szerkesztés]- Projektív koordináták.
- Súlyponti (baricentrikus) koordináták.
- Plücker-féle derékszögű homogén koordináták.
A projektív koordináta-rendszer az általános, a többi ennek speciális esete. (A magyar geometria tankönyvek egy része a nemzetközi terminológiával nem lévén összhangban, a Plücker-féle koordinátákat és csak ezeket nevezik homogénnek! )
Az egyenes (1D-tér) projektív koordinátái
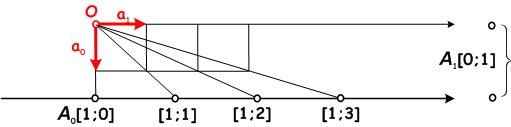
[szerkesztés]A projektív rendszert az egyenesen kívüli pontból induló két bázis-vektorral - - adjuk meg. A két bázis egy tetszőleges lineáris kombinációja egy olyan vektort ad meg, aminek egyenese az adott egyenest egy pontban metszi.
Definíció: Az rendezett pár elemei a pont koordinátái.
A definíció következménye: , mert a szorzó az és az vektor-komponenseket és ezzel a eredőt arányosan nyújtja meg. A vektor egyenese nem változik, ugyanazt a pontot jelöli ki.
Súlyponti koordinátákat akkor kapunk, ha a bázisvektorok „végpontja” az egyenesre esik.
Az egyenes Plücker-féle koordinátáit az egyenesre merőleges és párhuzamos, egyenlő hosszúságú bázis-pár szolgáltatja.
Egységpont: A bázis-vektorok összege olyan pontot jelöl ki, melynek koordinátái
A koordináta-rendszer az egyenes három (különböző) pontjának kijelölésével egyértelműen megadható:
- .
A sík (2D-tér) projektív koordinátái
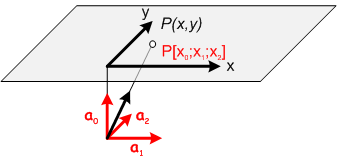
[szerkesztés]Az egyeneshez hasonlóan a sík koordináta-bázisát is egy külső pontból indítjuk. A különbség csupán a dimenzióban van. A síkbeli pontot a bázis lineáris kombinációjával adott eredő-vektor egyenese döfi ki. A pontkoordináták eszerint:
- .
A bázistól függetlenül is (anélkül, hogy a síkból kilépnénk) megadható a koordináta-rendszer a három alappont és az egységpont kitűzésével: . (Kikötés: A négy pont hármasával nem eshet egy egyenesbe!)
A súlyponti és a derékszögű homogén (az ábrán) koordináták ugyanúgy adódnak, mint az egyenesnél.
A 3D-tér projektív koordinátái
[szerkesztés]A térben a koordináta-rendszert a négy alappontjával (tetraéder) és az egységponttal tűzhetjük ki:
- .
A súlyponti rendszer egységpontját az alaptetraéder geometriai súlypontjában kell felvenni. A térbeli Plücker-féle rendszer alappontjai és egységpontja a Descartes-rendszerével esnek egybe.
Rácspontok
[szerkesztés]Az egyenes projektív rácspontjai azok, amelyeknek koordinátáinak hányadosa egész szám. Mivel a hányados (arány) nem kommutatív, kétféle rácspont-sorozatot kapunk. Az egyik az
A másik a reciprok rácsok sorozata
A (piros) projektív skála rácspontjai megfelelnek egy centrálisan vetített (kék) számegyenes rácspontjainak. A sík projektív rácspontjai és a rácsvonalak alkotják a Möbius-féle hálót, mely a perspektivikus térábrázolásban játszik szerepet.
Irodalom
[szerkesztés]- Hajós György: Bevezetés a geometriába - Tankönyvkiadó, Budapest, 1960.
- Coxeter, H.S.M.: Projektív geometria - Gondolat Kiadó, Budapest, 1986.
- Hack Frigyes: A 3D-grafika geometriai alapjai - ELTE-Mikrológia 43, 2002.






![{\displaystyle [x_{0};x_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6be8f47b9de1bd945a2d61f1225363b1c946d4c8)
![{\displaystyle [\mu x_{0};\mu x_{1}]=[x_{0};x_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5e6179e7f489a1afe10c7613fe5edebc65965cd)





![{\displaystyle E[1;1]=[\mu ;\mu ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4eaef6a6cfe8d22f6527822786539a207021b08d)



![{\displaystyle P[\mu x_{0};\mu x_{1};\mu x_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13afdb5342581a5c53e176eebb18b81ec937f142)




![{\displaystyle ...,[1;-1],[1;0],[1;1],[1;2],[1;3],...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8ef22ce8255eefc81ed4dbd70c6ce4ee25cb522)
![{\displaystyle ...,[-1;1],[0;1],[1;1],[2;1],[3;1],...}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6090b47de998ac46916c3ea26940cf6a68ea3f09)
