Logarléc

A logarléc (logaritmikus számolóléc) egy egyszerű kivitelű, mechanikus működésű analóg számológép, amely lehetővé teszi különböző matematikai műveletek gyors, 3-4 számjegy pontosságú elvégzését.

Szabványos logarlécek esetében az elvégezhető műveletek általában a következők: szorzás, osztás, négyzetre és köbre emelés, négyzet, illetve köbgyök vonása, logaritmusszámítás, trigonometriai függvények kiszámítása.

Működési elve

Összeadás

Ha két vonalzót egymás mellett elcsúsztatunk, akkor gyorsan tudunk két számot (távolságot) összeadni:

x+y=z

:

A logarléc működésének alapelve, hogy a számok szorzatát a számok logaritmusának összegzésével, a számok hányadosát a számok logaritmusának különbségével számítjuk ki.

A logarléc alapja két, egymáson elcsúsztatható logaritmikus skála. Ezt egészítik ki további skálák és egy átlátszó mozgatható ablak, amelyen hajszálvonalak segítik a skálákon található értékek pontos beállítását és leolvasását.

Szorzás

Két szám összeszorzásához a nyelv (mozgatható skála) kezdő értékét a fix skálán a szorzandó értékéhez kell mozgatni, és ezt követően a nyelven megkeresni a szorzót; a vele szemben a fix skálán található érték lesz a szorzat értéke.

\lg(x)+\lg(y)=\lg(xy)

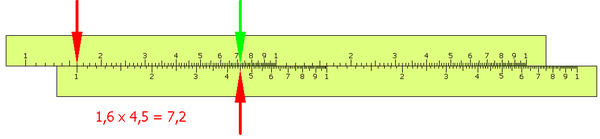
A szorzat értékének meghatározásához nem elegendő a skála leolvasása, a logarléc használójának fejben utánaszámolva meg kell állapítania a szorzat nagyságrendjét. Az ábra példáján 1,6 × 4,5 szorzatához ugyanúgy kell beállítani a skálát, mint 160 × 45 vagy 0,16 × 0,45 esetén.

Ha a skálák 1–10-ig készültek, könnyen kifuthatunk a tartományból. Például 2 × 7 = 14. Ilyenkor vagy olyan skálát használunk, amely 1-100-ig van beosztva, mint az ábrán, vagy a nyelv másik irányba való mozgatásával keressük meg a szorzatot.

Osztás

Osztáskor a nyelven (mozgó skálán) meg kell keresni az osztót, ezt szembe kell állítani a fix skálán az osztandóval, és a nyelv kezdeti értékénél találjuk a fix skálán a hányados értékét.

\lg(x)-\lg(y)=\lg(x/y)

Más skálák

Az alapvető logaritmikus skálákon kívül a gyakorlatban használatos logarlécek más skálákat is tartalmaznak.

A kétszeres léptékű és egyszeres léptékű logaritmikus skálák összevetésével könnyen lehet négyzetre emelni és négyzetgyököt vonni. Arra azonban vigyázni kell, hogy például 4 és 40 négyzetgyökét máshol kell keresni a felső skálán. Négyzetgyökvonásnál a számot a tizedesvesszőtől számítva két számjegyből álló csoportokra bontjuk, és ahol a felosztás már nem folytatódhat, ott látjuk, melyik mezőben kell keresni a négyzetgyököt.

Háromszoros léptékű logaritmikus skálával ehhez hasonlóan köbgyököt lehet vonni. Gyakorlati számításokhoz fontosak a szögfüggvények, a szinusz, koszinusz és tangens skálák. Kis szögek szinusz és tangens skálája is található a legtöbb logarlécen.

A fordított logaritmikus skála 1/x számítását könnyíti meg.

Lineáris skála segítségével a számok 10-es alapú logaritmusát lehet megkeresni, log-log skála pedig a természetes alapú logaritmus keresését és tetszőleges hatványozást tesz lehetővé.

A leggyakrabban használatos skálák

A, B	Kétszeres léptékű logaritmikus skálák, az előbbi a testen, az utóbbi a nyelven. Négyzetre emelésre és négyzetgyökvonásra használatosak.
C, D	A klasszikus logaritmikus skálák.
K	Háromszoros léptékű logaritmikus skála.
CF, DF	A szimpla logaritmikus skála π-vel szorozva.
CI, DI, DIF	Logaritmikus skála reciproka. Gyakorlatilag a logaritmus skála tükrözöttje.
S	Szinusz skála általában 6°-tól 90°-os értékekig.
T₁, T₂	Tangens skálák, az előbbi 6° és 45°, az utóbbi 45° és 84° között.
ST, SRT	Skála kis szögek tangensének, szinuszának és fok-radián átváltásának számításához.
L	A C és a D skála logaritmusa. Gyakorlatilag egy lineáris skála 0 és 1 között.
LL_n	3 vagy 4 db log-log skála. Könnyen számítható vele valós számokkal történő hatványozás.
Ln	Természetes alapú logaritmus skála, ez is lineáris 0 és 2,3 között.

Skálák a K&E 4081-3 logarléc elején és hátulján

Gyakorlati kivitel

A logarléceket régebben fából, majd fa és műanyag kombinációjából készítették, legújabban teljesen műanyagból vagy fémből állnak. A fém logarlécek ugyan lehetővé teszik a pontosság növelését, de a csillogó felület és a fémes szín miatt a leolvasás nehezebb és így használatuk fárasztóbb. A közönséges logarlécek leolvasási pontossága általában két számjegy és a harmadikat a felhasználó megbecsülte, a speciális logarlécek pontossága ennek kétszerese is lehet. Európában a szabványos hossz 25 cm, emellett készültek 12,5 cm-es (zseb-) és 50 cm-es (irodai) logarlécek is. Angolszász országokban a szabványos logarléc hossza 10, 5, illetve 12,5 hüvelyk (25,4, 12,7 és 31,8 cm).

A skáláról való kifutás elkerülhető az ún. körlogarléccel, ahol a skálákat két koncentrikus kör alakú tárcsára viszik fel. Ennek előnye még, hogy hosszabb skálát harmad akkora főméretekkel lehet készíteni, mint a közönséges logarlécekkel. Ennek ellenére a logarlécek túlnyomó többsége egyenes típusú.

Különböző szakmák egyedi céljainak megfelelő speciális logarléceket is készítettek, így például létezett különböző, mérnököknek, bankoknak és pénzügyi célokra szánt logarléc, de például a II. világháború amerikai bombázópilótái is használtak különleges logarléceket.

Története

A logarlécet 1620-1630 között találták fel, miután John Napier publikálta a logaritmusról szóló alapvető művét. Az oxfordi egyetemen Edmund Gunter feltalált egy eszközt, mely egy logaritmikus skálából és mérőeszközökből állt és amellyel szorozni és osztani lehetett. 1630-ban a cambridge-i William Oughtred készített egy körlogarlécet, és 1632-ben egyesítette találmányát Gunter eszközével, ezzel létrejött a mai értelemben vett logarléc. Oughtred sokáig nem publikálta találmányát, hasonlóan a kortárs Newtonhoz, aki forradalmian új fizikai elméleteit évekig nem merte nyilvánosságra hozni, és később kemény harcot folytatott az elsőbbségért egy korábbi tanítványával, Richard Delamainnel.

1722-ben Warner bevezette a négyzet- és köbskálát, 1755-ben Everard az inverz skálát (1/x), 1815-ben pedig Peter Roget feltalálta a log-log skálát. A 19. században a logarléc használata széles körben elterjedt Európában. A mérnöki számítások túlnyomó részét logarléc segítségével végezték. Ehhez természetesen olyan számítási eljárásokra volt szükség, melyek nem voltak érzékenyek a kerekítési hibára.

Az 1970-es, 1980-as években a logarléc végleg elavult, felváltották a különböző tudományos kalkulátorok, 1974-től a logarlécek gyártói sorozatban mentek csődbe.^[1]^[2]^[3]^[4] Ezzel az emberiség kultúrájának egy kiemelkedő találmánya került múzeumba.

A legutolsó speciális logarlécek az amerikai Apollo-program számára készültek, és a programban részt vevő űrhajósok használták azokat.

A logarlécet mára az elektronikus eszközök teljesen kiszorították, csak múzeumokban és idősebb mérnökök gyűjteményeiben lelhetők fel.

Előnyök

A logarléc korlátozott pontossága nem mindig hátrány. A legtöbb mérnöki számításnál a kiinduló adatok pontossága nem nagyobb annál, mint amit a logarléc nyújt. A számológép 7–9 jegyű pontossága azt az illúziót kelti, hogy nagyon pontos eredményre jutunk, holott a bemenő adatok valójában pontatlanok. Ettől a hibás illúziótól megóv a logarléc használata.
A logarléccel való munka megköveteli a nagyságrendek fejben történő ellenőrzését. Ez nagy ellenőrzési biztonságot ad a számítások során: aki logarléccel dolgozik, nem követ el olyan jellegű nagyságrendi hibát, ami a modern számítástechnikában (adatok elütése miatt) könnyen bekövetkezhet.
A gyakorlati számítást igen sok apró fogás könnyíti és gyorsítja logarléccel. Például, ha egy számot sok számmal akarunk egymást követően szorozni, a skálát elég egyszer beállítanunk, utána csak az ablakot kell mozgatni, és az eredményeket leolvasni.
Mivel a logarléc működése mechanikus, nem igényel áramforrást.
A logarlécek annyira szabványosak, hogy egy új logarléc használatához semmiféle utasítás nem szükséges.

Hátrányok

Ez a szakasz egyelőre üres vagy erősen hiányos. Segíts te is a kibővítésében!

A számítás pontossága függ a logarléc hosszától.^[5]

Általánosítások

Az eddig ismertetett logaritmikus skálák helyett a csúszkákra tetszőleges más skálákat helyezve más képleteket is kiszámolhatunk gyorsan.

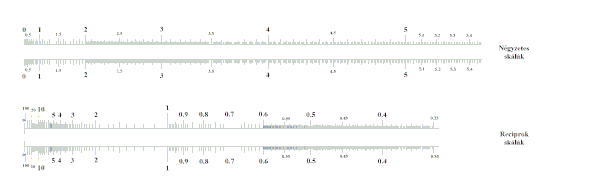
Például, négyzetes skálákkal az $x^{2}+y^{2}=z^{2}$ összefüggés, reciprok skálákkal az ${\frac {1}{x}}+{\frac {1}{y}}={\frac {1}{z}}$ összefüggés alapján kereshetjük meg $z$ -t $x$ és $y$ ismeretében, egyetlen léceltolással.

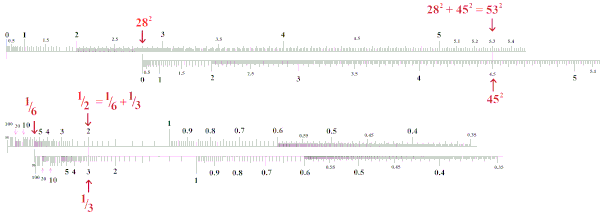
A reciprok és négyzetes skálák használata: erről részletesebben itt^[6]^[7]^[8] olvashatunk.

Jegyzetek

A Wikimédia Commons tartalmaz Logarléc témájú médiaállományokat.

↑ Writing and reading across the curriculum. Little, Brown, 273. o. (1982) „Then, just a decade ago, the invention of the pocket calculator made the slide rule obsolete almost overnight...”
↑ e: The Story of a Number. Princeton University Press, 16. o. (2009). ISBN 9780691141343 „Then in the early 1970s the first electronic hand-held calculators appeared on the market, and within ten years the slide rule was obsolete.”
↑ Inventions that Changed the World. Futura, 157. o. (2007). ISBN 9780708807866 „With the invention of the calculator the slide rule became instantly obsolete.”
↑ Beyond calculation: the next fifty years of computing. Springer, xiv. o. (1998). ISBN 9780387985886 „The first hand calculator appeared in 1972 and made the slide rule obsolete overnight.”
↑ A logarléc
↑ Szalkai István: Mit tudhat egy számolóléc?, KöMaL 1977. http://math.uni-pannon.hu/~szalkai/Szalkai-1977-KoMaL.pdf, http://db.komal.hu/scan/1977/04/97704146.g4.png http://db.komal.hu/scan/1977/04/97704151.g4.png
↑ Szalkai,I.: General Two-Variable Functions on the Slide Rule, Journal of the Oughtred Society, 27:1, Spring 2018, pages 14-18. http://www.oughtred.org/jos/pages/JOS_2018_Vol_27_1_TOC.jpg
↑ Szalkai,I.: General Two-variable Functions on the Slide-rule, http://arxiv.org/abs/1612.03955

Források

Sárközy Zoltán: Műszaki táblázatok és képletek. Műszaki Könyvkiadó, Budapest, 1977. ISBN 963-10-1241-7
www.arithmomuseum.com: Virtuális logarléc-múzeum. www.arithmomuseum.com. (Hozzáférés: 2022. május 27.)

További információk

Online szimulátorok:

Sag Milling's Online Sliderule – Teljesen működőképes logarléc
Körlogarléc (Flash) – A Center for Technology and Teacher Education, University of Virginia-tól
Logarléc Java szimulációja– Szerző: Andrew Davie

Informatikai portál • összefoglaló, színes tartalomajánló lap

[1] Writing and reading across the curriculum. Little, Brown, 273. o. (1982) „Then, just a decade ago, the invention of the pocket calculator made the slide rule obsolete almost overnight...”

[2] e: The Story of a Number. Princeton University Press, 16. o. (2009). ISBN 9780691141343 „Then in the early 1970s the first electronic hand-held calculators appeared on the market, and within ten years the slide rule was obsolete.”

[3] Inventions that Changed the World. Futura, 157. o. (2007). ISBN 9780708807866 „With the invention of the calculator the slide rule became instantly obsolete.”

[4] Beyond calculation: the next fifty years of computing. Springer, xiv. o. (1998). ISBN 9780387985886 „The first hand calculator appeared in 1972 and made the slide rule obsolete overnight.”

[5] A logarléc

[6] Szalkai István: Mit tudhat egy számolóléc?, KöMaL 1977. http://math.uni-pannon.hu/~szalkai/Szalkai-1977-KoMaL.pdf, http://db.komal.hu/scan/1977/04/97704146.g4.png http://db.komal.hu/scan/1977/04/97704151.g4.png

[7] Szalkai,I.: General Two-Variable Functions on the Slide Rule, Journal of the Oughtred Society, 27:1, Spring 2018, pages 14-18. http://www.oughtred.org/jos/pages/JOS_2018_Vol_27_1_TOC.jpg

[8] Szalkai,I.: General Two-variable Functions on the Slide-rule, http://arxiv.org/abs/1612.03955

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]