Komplementer színezés
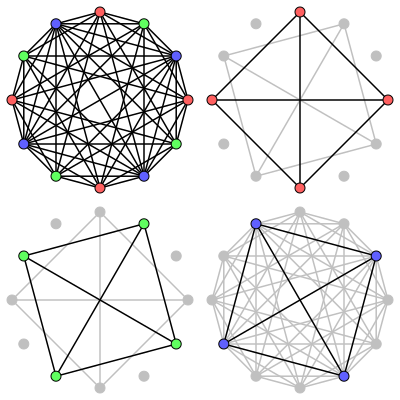
A matematika, azon belül a gráfelmélet területén egy G gráf komplementer színezése, esetleg koszínezése (cocoloring) alatt a csúcsok olyan színezését értjük, melynél minden színosztály vagy G-ben, vagy G komplementerében alkot független csúcshalmazt. Ezzel egyenértékű megfogalmazás szerint G csúcsainak olyan színezése, ahol a színosztályok vagy klikket, vagy független csúcshalmazt feszítenek ki. A G gráf z(G) komplementer kromatikus száma (cochromatic number) a G komplementer színezéséhez szükséges legkevesebb színek száma. A 2 komplementer kromatikus számú gráfok éppen a páros gráfok, a páros gráfok komplementerei és a split gráfok.
Mivel a követelmény, hogy minden színosztály klikk vagy független csúcshalmaz legyen, gyengébb a jó színezésnél megkívántnál (ahol minden színosztály független csúcshalmaz) és erősebb mint a részszínezés esetében (ahol minden színosztálynak klikkek diszjunkt uniójának kell lennie), ezért G komplementer kromatikus száma kisebb vagy egyenlő G kromatikus számánál, de nagyobb vagy egyenlő G részkromatikus számánál.
A komplementer színezést elsőként (Lesniak & Straight 1977) tanulmányozta és nevezte el. (Jørgensen 1995) adja meg a kritikus 3-komplementer kromatikus gráfok jellemzését, míg (Fomin, Kratsch & Novelli 2002) a gráfok komplementer kromatikus számát közelítő algoritmusokat ír le. (Zverovich 2000) definiál egy „perfekt komplementer kromatikus gráfok” nevű gráfosztályt (annak analógiájára, ahogy a perfekt gráfokat definiálják a jó színezés segítségével), és megadja ezen gráfok tiltott gráfok szerinti osztályozását.
Fordítás
[szerkesztés]- Ez a szócikk részben vagy egészben a Cocoloring című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek
[szerkesztés]- Fomin, Fedor V.; Kratsch, Dieter & Novelli, Jean-Christophe (2002), "Approximating minimum cocolourings", Inf. Process. Lett. 84 (5): 285–290, DOI 10.1016/S0020-0190(02)00288-0.
- Gimbel, John & Straight, H. Joseph (1987), "Some topics in cochromatic theory", Graphs and Combinatorics 3 (1): 255–265, DOI 10.1007/BF01788548.
- Jørgensen, Leif K. (1995), "Critical 3-cochromatic graphs", Graphs and Combinatorics 11 (3): 263–266, DOI 10.1007/BF01793013.
- Lesniak, L. & Straight, H. J. (1977), "The cochromatic number of a graph", Ars Combinatoria 3: 39–46.
- Straight, H. J. (1979), "Cochromatic number and the genus of a graph", Journal of Graph Theory 3 (1): 43–51, DOI 10.1002/jgt.3190030106.
- Zverovich, Igor V. (2000), Perfect cochromatic graphs, Research report RRR 16-2000, Rutgers University Center for Operations Research, <http://rutcor.rutgers.edu/pub/rrr/reports2000/16.ps>. Hozzáférés ideje: 2018-01-17.
