Ekvipartíció-tétel

Az ekvipartíció-tétel a klasszikus statisztikus mechanika egyik általános tétele, mely egy rendszer hőmérséklete és általános energiája között teremt összefüggést. Más neveken is ismert mint pl. ekvipartíció-törvény, az energia ekvipartíciója vagy csak ekvipartíció.

Az alapgondolat és példák

Az „ekvipartíció” egyenlő részekre való bontást jelent a latin 'equi' és a 'partitionem' szavakból eredően.

Az ekvipartíció eredeti koncepciója az volt, ha egy rendszer elérte a termikus egyensúly állapotát, akkor a rendszer teljes kinetikus energiája átlagosan egyenlő részekből áll. Az ekvipartíció számszerű jóslatokat is lehetővé tesz ezekre az energiákra. Az egyatomos gázok pontszerű részecskéi energiájukat haladási mozgási energia formájában hordozzák.

Például egy nemesgáz minden atomjának - T hőmérsékleten, termikus egyensúlyi állapotban - átlagos mozgási energiája (3/2)k_BT, ahol k_B a Boltzmann állandó. Ebből következően, mivel m tömeggel rendelkező, egyenes vonalban, egyenletes sebességgel mozgó test haladási kinetikus energiája $E_{t}={\frac {1}{2}}mv_{TKP}^{2}$ (ahol: E_t a haladási kinetikus energia, m a test tömege, v_TKP a test tömeg-középpontjának sebessége), a xenon nehezebb atomjainak átlagos sebessége például kisebb, mint a hélium gáz könnyebb atomjai sebessége ugyanazon a hőmérsékleten.

Nemesgázok sebessége a Maxwell-Boltzmann eloszlás szerint

Az ábra négy nemesgáz atomjainak sebességét mutatja a Maxwell–Boltzmann eloszlás szerint. Az indexben az elemek tömege látható.

Az ekvipartíció tétele azt mondja ki, hogy minden szabadságfokhoz (sebesség-jellemzőhöz), egy molekulára átlagosan ¹⁄₂k_BT mozgási energia tartozik, ezért ¹⁄₂k_BT részben járul a rendszer hőkapacitásához.

Az elmélet korlátai

Az ekvipartíció elmélet nem működik, amikor a termikus energia k_BT jelentősen kisebb, mint az energiaszintek közötti tér. Hibás volt az a feltételezés, hogy az energiaszintek folytonos közeget alkotnak. Ezért nem is lehetett megmagyarázni a hőkapacitások viselkedését és a feketetest-sugárzást; szükség volt egy új elméletre, a kvantummechanika és a kvantumtérelméletre.

Katódlumineszcens mikroszkóp

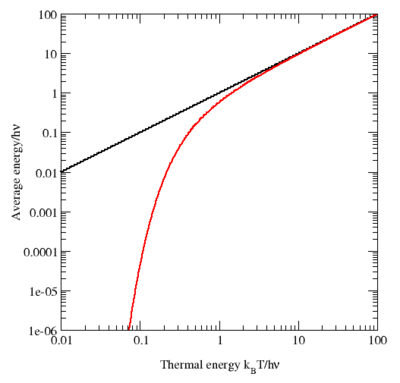
Az ábrán logaritmikus osztásban egy kvantummechanikai oszcillátor átlagos energiája látható a hőmérséklet függvényében. Összehasonlításképpen fekete színnel az ekvipartíció által jósolt értékek láthatók. Magas hőmérsékleten a két görbe hasonló értéket mutat, alacsony hőmérsékleteken, amikor k_BT << hν - ahol v (nü) az oszcillátor frekvenciája -, a kvantummechanikai érték jóval gyorsabban csökken. Ez megoldja az ultraibolya katasztrófa problémáját. Egy adott hőmérsékleten nagyfrekvenciás módusban, ahol hν >> k_BT, az energia majdnem zéró.

Az ekvipartíció elmélet hibáját illusztrálandó, tekintsünk egy harmonikus oszcillátort. Elhagyva az irreleváns zéro-pont energia kifejezést, a kvantum energia szintje E_n = nhν , ahol h a Planck-állandó, ν az oszcillátor alapfrekvenciája és n egész szám (n = 1, 2, 3...). Egy adott energiaszint valószínűsége a kanonikus valószínűség-eloszlásban a Boltzmann-tényezővel kifejezve:

$P(E_{n})={\frac {e^{-n\beta h\nu }}{Z}},$

ahol β = 1/k_BT és a Z nevező a partíciófüggvény, itt egy mértani sorban:

$Z=\sum _{n=0}^{\infty }e^{-n\beta h\nu }={\frac {1}{1-e^{-\beta h\nu }}}.$

általános energiája:

$\langle H\rangle =\sum _{n=0}^{\infty }E_{n}P(E_{n})={\frac {1}{Z}}\sum _{n=0}^{\infty }nh\nu \ e^{-n\beta h\nu }=-{\frac {1}{Z}}{\frac {\partial Z}{\partial \beta }}=-{\frac {\partial \log Z}{\partial \beta }}.$

Z-t behelyettesítve adódik a végső eredmény:

$\langle H\rangle =h\nu {\frac {e^{-\beta h\nu }}{1-e^{-\beta h\nu }}}.$

Magas hőmérsékleteken, amikor a termikus energia k_BT jóval nagyobb, mint a hν érték az energia szintek között, a βhν exponenciális argumentum jóval kisebb, mint egy, és az átlagos energia k_BT lesz, az ekvipartíció elméletnek megfelelően. Azonban alacsony hőmérsékleteken, amikor hν >> k_BT, az átlagos energia zéróhoz tart – a magas frekvenciás energiaszintek „kifagynak”.

Egy másik példa: egy hidrogénatom belsőleg gerjesztett elektronikus állapotai nem tudnak hozzájárulni a gáz hőjéhez, mert a termikus energia k_BT (közel 0,025 eV) jóval kisebb, mint az alacsonyabb és a következő magasabb energia szint (kb. 10 eV) közötti rés.

Hasonló meggondolások érvényesek, amikor az energiaszint közti rés jóval nagyobb, mint a termikus energia.

Például Albert Einstein ezzel magyarázta, illetve oldotta meg a ultraibolya katasztrófa problémáját.

A paradoxon azért jöhetett létre, mert egy zárt konténerben az elektromágneses térnek végtelen sok független módusa van, mindegyik egy harmonikus oszcillátornak tekinthető. Ha viszont minden elektromágneses módus átlagos energiája k_BT, akkor végtelen nagy energiának kell lennie a konténerben. Azonban a fenti érvelés okán a nagyfrekvenciás módusok átlagos energiája tart a zérushoz, amikor ν tart a végtelenbe; ezen felül Planck törvénye a feketetest sugárzásról hasonló érvelést használ. Más, bonyolult kvantumhatások is az ekvipartíció elméletének korrekciójához vezetnek, mint a kvantumelmélet azonos részecskék és a folytonos szimmetria elméletei.

További információk

• Huang, K. Statistical Mechanics, 2nd, John Wiley and Sons, 136–138. o. (1987). ISBN 0-471-81518-7 
• Landau, LD, Lifshitz EM. Statistical Physics, Part 1, 3rd, Pergamon Press, 129–132. o. (1980). ISBN 0-08-023039-3 
• Mohling, F. Statistical Mechanics: Methods and Applications. John Wiley and Sons, 137–139, 270–273, 280, 285–292. o. (1982). ISBN 0-470-27340-2 
• Pathria, RK. Statistical Mechanics. Pergamon Press, 43–48, 73–74. o. (1972). ISBN 0-08-016747-0 
• Pauli, W. Pauli Lectures on Physics: Volume 4. Statistical Mechanics. MIT Press, 27–40. o. (1973). ISBN 0-262-16049-8 
• Tolman, RC. Statistical Mechanics, with Applications to Physics and Chemistry. Chemical Catalog Company, 72–81. o. (1927)  ASIN B00085D6OO
• Tolman, RC. The Principles of Statistical Mechanics. New York: Dover Publications, 93–98. o. (1938). ISBN 0-486-63896-0 

• Marx György. Kvantummechanika. Műszaki Kiadó (1957) 
• Sailer Kornél. Bevezetés a kvantummechanikába. egyetemi jegyzet 
• Landau-Lifsic. Elméleti fizika III:Kvantummechanika. Tankönyvkiadó (1978). ISBN 963-17-3259-2 
• Callen, Herbert B.. Thermodynamics and an Introduction to Thermostatistics (2nd ed.). Wiley (1985). ISBN 0-471-86256-8 
• Kroemer, Herbert; Kittel, Charles. Thermal Physics (2nd ed.). W. H. Freeman Company (1980). ISBN 0-7167-1088-9 
• https://web.archive.org/web/20090516232442/http://www.szgti.bmf.hu/fizika/feketetest/
• https://web.archive.org/web/20100201140641/http://lexikon.fazekas.hu/227
• http://sdt.sulinet.hu/Player/Default.aspx?g=5dc5b33f-9517-4d32-9d40-388d4b8c4275&cid=277d557d-03c6-4fb7-b2b2-6c5d3e5ac909