Egy- és kétoldalas próbák
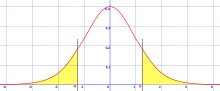
A statisztikai hipotézisvizsgálatokban az egy- és kétoldalas próbák különböző megközelítései egy paraméter statisztikai szignifikanciájának meghatározásában. A kétoldali próba abban az esetben megfelelő, ha a becsült érték lehet nagyobb és kisebb is, mint a referenciaérték, például ha egy tesztkitöltő teljesíthet a történelmi átlag alatt és felett is. Az egyoldali teszt akkor alkalmazandó, amikor a becsült érték a referenciaértéktől csak egy irányban térhet el, például ha arra vagyunk kíváncsiak, hogy egy gép több mint 1%-nyi hibás terméket hoz-e létre. A próbák neve a mintavételi eloszlás oldalaira utal, ahol az értékek gyakorisága igen kicsi, és gyakran a nullához közelít.
Alkalmazási területei
[szerkesztés]Az egyoldalas próbát olyan aszimmetrikus eloszlásokban alkalmazhatjuk, amelyeknek csak egy oldala van, például a khí-négyzet eloszlásban, vagy alkalmazhatjuk egy kétoldalú eloszlás (például normális eloszlás) egyik oldalára, ha megjelöljük a próba irányát. Kétoldalas próbát csak abban az esetben alkalmazhatunk ha az eloszlásnak két oldala van, így mindkét irányban lehet szignifikáns értékünk.[1][2][3]
Ronald Fisher megközelítése szerint a nullhipotézis elvethető, ha a statisztikai próba p-értéke megfelelő mértékben szélsőséges, és ezzel a véletlen eredmény magasan valószínűtlennek ítélhető. Egy egyoldalas próbában a ‘szélsőség’ iránya a próba elvégzése előtt dől el, tehát vagy kellően kicsi az érték, vagy kellően nagy – a másik irányban lévő értékek nem tekinthetők szignifikánsnak.[4] A kétoldalas tesztekben mindkét irányban szignifikáns lehet a szélsőséges érték. Egy kétoldalas statisztikai próba adott adatokkal és szignifikanciaszinttel egy ezzel megegyező egyoldalas tesztben ugyanazokkal az adatokkal, vagy kétszer szignifikánsabb (a p-érték fele) – ha az adatok a tesztben meghatározott irányban vannak –, vagy egyáltalán nem szignifikáns, hiszen a tesztben meghatározott iránnyal ellentétesek az adataink.
Például, ha pénzfeldobáskor azt akarjuk tesztelni, hogy a pénz cinkelt-e a fej irányába, az egy egyoldalas próba, amelyben ha minden pénzfeldobásunk fej, az adatok magasan szignifikánsak lennének, míg ha minden pénzfeldobásunk írás lenne, akkor nem lenne szignifikáns az eredményünk. Ezzel szemben, ha azt teszteljük, hogy cinkelt-e akármelyik irányba, az egy kétoldalas próba, amelyben mind a fej, mind az írás extrém gyakorisága szignifikanciát jelezne. Az egészségügyi kutatásban, ha arra vagyunk kíváncsiak, hogy a kezelés eredménye jobb-e a véletlenszerű eredménynél, akkor egyoldalas próbát csinálunk; a véletlenszerűnél rosszabb is szolgálhat fontos adatokkal, ebben az esetben kétoldalas próbát kell alkalmaznunk, amelyben azt vizsgáljuk, hogy eltér-e a kezelés eredménye a véletlenszerűtől.[5]
A pénzfeldobásos példa
[szerkesztés]Pénzfeldobáskor a nullhipotézis Bernoulli-próbák sorozata 0,5-ös valószínűséggel, egy olyan véletlenszerű változót (X) magába foglalva, amely vagy 1 (fej), vagy 0 (írás) értékeket vehet fel (röviden, a nullhipotézisünk az, hogy 50-50% esély van mindkét értéket felvennie a változónknak). Ha arra vagyunk kíváncsiak, hogy a fej irányába van-e cinkelve a pénzünk, egy egyoldalas próbát kell alkalmaznunk – tehát csak nagy fej-többségben lesz szignifikáns a próbánk. Ebben az esetben, ha az adathalmazunk 5 fejből áll, 1-es mintaátlaggal, amelynek a valószínűsége 1/32 = 0,03125 (5 egymás után pénzfeldobás két lehetséges kimenetellel – ((1/2)^5=1/32). A p-érték tehát körülbelül 0,03 lenne, amely szignifikanciát jelez, ha a 0,05-ös határértékkel számolunk. Ezzel szemben, ha azt teszteljük, hogy a pénzérme bármelyik irányba cinkelve van-e, egy kétoldalas tesztet alkalmaznánk, amelyben 5 fej (1-es mintaátlag) és 5 írás (0-ás mintaátlag) is ugyanannyira szélsőséges lenne, ebben az esetben a p-érték 2/32 lenne (0,0625), amely már nem számít szignifikánsnak a 0,05-ös határértékkel számolva.
Története
[szerkesztés]
A p-értéket Karl Pearson[6] vezette be a Pearson-féle khí-négyzet próbában, ahol a p-értéket egy adott értéktől való eltérés valószínűségeként határozta meg. Ez egy egyoldalas meghatározás, mert a khi-négyzetes eloszlás aszimmetrikus, amely vagy nullát, vagy egyet feltételez, tehát az eloszlásnak csak egy oldala van. A próba az adataink eloszlásának egy hipotetikus eloszlásra való illeszkedését vizsgálja.

Az egyoldalas és kétoldalas tesztek elkülönítését Ronald Fisher népszerűsítette a nagy sikerű Statistical Methods for Research Workers[7] című könyvében, ahol leginkább a normáleloszlásra alkalmazta, amely egy szimmetrikus eloszlás két oldallal.
Fisher az oldalak kiszámításának fontosságát hangsúlyozta a The Design of Experiments (1935)[8] című könyvében is, ahol elmagyarázta, hogy egy specifikus adathalmaz lehet kellően valószínűtlen, de ha az a kérdésfelvetésünkkel ellentétes irányú, nem lehet szignifikánsnak tekinteni.
Jegyzetek
[szerkesztés]- ↑ Kock, N. (2015). One-tailed or two-tailed P values in PLS-SEM? International Journal of e-Collaboration, 11(2), 1-7.
- ↑ Mundry, R. (1998). „Use of Statistical Programs for Nonparametric Tests of Small Samples Often Leads to Incorrect P Values: Examples from Animal Behaviour”. Animal Behaviour 56 (1), 256–259. o. DOI:10.1006/anbe.1998.0756.
- ↑ Pillemer, D. B. (1991). „One-versus two-tailed hypothesis tests in contemporary educational research”. Educational Researcher 20 (9), 13–17. o. DOI:10.3102/0013189X020009013.
- ↑ John E. Freund, (1984) Modern Elementary Statistics, sixth edition. Prentice Hall.
- ↑ J M Bland, D G Bland (BMJ, 1994) Statistics Notes: One and two sided tests of significance
- ↑ Pearson, Karl (1900). „On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling”. Philosophical Magazine 50 (302), 157–175. o. DOI:10.1080/14786440009463897.
- ↑ Fisher, Ronald. Statistical Methods for Research Workers. Edinburgh: Oliver & Boyd (1925). ISBN 0-05-002170-2
- ↑ Fisher, Ronald A.. The Design of Experiments, 9th, Macmillan [1935] (1971). ISBN 0-02-844690-9
Fordítás
[szerkesztés]Ez a szócikk részben vagy egészben az One- and two-tailed tests című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
