A termodinamika második főtétele

A természetben lejátszódó folyamatok többsége egy irányban zajlik le, fordított irányban maguktól nem mennek végbe (külső hatás egyes esetekben megfordíthatja a folyamatot). Az ilyen folyamatokat irreverzibilis folyamatoknak nevezzük. Például ha összetöltünk hideg és meleg vizet, akkor a langyos keverékből, amit kapunk, külső hatás nélkül az eredeti hideg és meleg víz nem nyerhető vissza. Egy másik példa, ha egy talajon csúszó testet nézünk, a test a súrlódás hatására egy idő után megáll, közben pedig hő termelődik. A test sohasem fog magától felgyorsulni a lehűlése árán. Mindkét fordított folyamat eleget tenne a termodinamika első főtételének, de mégsem történnek meg.

A hő a meleg víztől átadódik a hideg víznek

A fenti példákat általánosabban is megfogalmazhatjuk. Az első példa kapcsán kijelenthetjük, hogy hő önként (spontán lezajló folyamatokban) csak melegebb testről hidegebbre mehet át, vagyis a természetben a hőmérsékletek arra törekednek, hogy kiegyenlítődjenek. A második példa kapcsán megfogalmazható, hogy nem lehet olyan gépet készíteni, amely hőtartály lehűlése révén munkát végezne. Ezek az állítások a termodinamika második főtételének legkorábbi, egymással ekvivalens megfogalmazásai.

A második főtétel a termodinamikai folyamatok eléggé nyilvánvaló irányát mutatja, mélyebb tartalma azonban csak a molekuláris hőelmélet keretében érthető meg. Az egyik általános szemléletű megfogalmazás szerint azt mondja ki, hogy egy izolált (elszigetelt) rendszer állapota termikus egyensúly felé halad.

Találóan nevezték az l. főtételt az elsőfajú, a II. főtételt a másodfajú perpetuum mobile lehetetlensége elvének. Másodfajú perpetuum mobile lenne pl. az a gép, amely minden befektetett hőt körfolyamatokkal folyamatosan munkavégzésre fordítana. A körfolyamatok tárgyalása során látszik, hogy ilyen gépet akkor sem lehetne készíteni, ha a súrlódást teljesen ki tudnánk küszöbölni, mert a hő egy része mindig elvész, vagyis a befektetett hőnek csak egy részét lehet munkává alakítani.

A termodinamika első főtételének elégtelensége

A természetben lejátszódó folyamatok mindegyike igazolja a termodinamika első főtételét. Így az első főtétel egyik következménye, az elsőfajú örökmozgó lehetetlensége is igazolt.

A valóságban elképzelhetők olyan fizikai folyamatok, amelyek az első főtételének nem mondanak ellent, de gyakorlatilag nem valósíthatók meg. Például az első főtételnek nem mond ellent egy olyan hőerőgép, amely egyetlen hőforrás energiáját használja fel, például tengerek termikus energiáját. Továbbá ismert, hogy két test érintkezésekor a hő a magasabb hőmérsékletű testről az alacsonyabb hőmérsékletű testre spontán megy át, de az ellentétes irányú spontán hőátadás nem valósítható meg annak ellenére, hogy nem mond ellent az első főtételnek.

Az elmondottakból következik, hogy a természeti folyamatok irreverzibilisek, de az irreverzibilitás ténye nem következik az első főtételből.

Az első főtételből következik a munka és a hőmennyiség egyenértékűsége, továbbá az is, hogy a munka teljesen hővé alakítható, tehát ez a folyamat nem korlátozott. Gyakorlatilag nagyon fontos a fordított folyamat, a hő munkává való átalakítása, mivel a természeti energiaforrások nagy része bizonyos fűtőanyagok energiájához kapcsolt. A tapasztalat szerint a fűtőanyagok elégetésekor felszabaduló hőmennyiség csak részben alakítható munkává annak ellenére, hogy a teljes átalakítás nem mondana ellent a termodinamika első főtételének.

Összefoglalva az eddigieket következik, hogy a termodinamika első főtétele nem elegendő a természeti folyamatok leírására vagyis felmerül egy újabb főtétel szükségessége. Ez lesz a termodinamika második főtétele.

Egyetlen hőforrásból működő hőerőgép megvalósításával sokan próbálkoztak, de az igyekezetet minden esetben kudarc kísérte. E kísérletek következményeként megfogalmazható a következő tétel: nem lehetséges olyan mechanikai munkát termelő gép, amely egyetlen hőforrással működne. Az ilyen típusú gépet Ostwald másodfajú örökmozgónak nevezte (másodfajú perpetuum mobile). A másodfajú örökmozgó lehetetlensége tulajdonképpen a termodinamika második főtételének egyik megfogalmazása. A második főtételnek ebből a megfogalmazásából következik, hogy szerkeszthető olyan berendezés amely, két hőforrással folyamatos munkavégzésre képes.

Megfogalmazások

A tételnek számos megfogalmazása létezik.

Clausius-féle megfogalmazás

Az első megfogalmazójaként számon tartott Rudolf Clausius a hő fogalmának segítségével a hőcsere irányát határozta meg:

Nincs olyan folyamat, amelynek eredményeképpen a hő az alacsonyabb hőmérsékletű rendszer felől a magasabb hőmérsékletűnek adódik át. Másképp fogalmazva, a hő nem mehet át spontán módon alacsonyabb hőmérsékletű testről magasabb hőmérsékletű testre.

Carnot-féle megfogalmazás

Carnot-körfolyamat a p-V síkban, ahol Q1 a felvett hő, míg Q2 a leadott

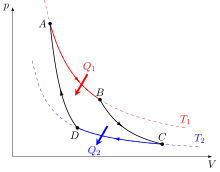
Két adott hőtartály között működő hőerőgépek közül a reverzibilis Carnot-ciklus szerint működő hőerőgépnek maximális a termikus hatásfoka. A Carnot-ciklus két izotermából és két adiabatikus folyamatból áll.

Kelvin-féle megfogalmazás

Lord Kelvin, a munka fogalmát felhasználva, a következőképpen fogalmazott:

A hő nem alakítható teljes mértékben munkává semmilyen ciklikus folyamaton keresztül.

Thomson-, majd később Planck-féle megfogalmazás

A termodinamika I. főtétele szerint a hő felvételével vagy hő leadásával kapcsolatos folyamatok az energiamegmaradási törvénynek megfelelően játszódnak le. Ebből azonban nem derül ki, hogy a folyamat valójában milyen irányban megy végbe, pl. ha egy acélgolyót leejtünk, a helyzeti energiája végül teljes egészében hővé alakul át. Sohasem tapasztalható azonban a jelenség fordítottja. Vagyis a golyó "magától", lehűlés árán nem emelkedik a magasba. Ezek szerint tehát lehetetlen olyan gépet, berendezést készíteni. amely minden más változtatás nélkül egy “hőtartályból" (pl. a légkörből, vagy a tengerek vizéből) elvont hőt teljes egészében munkává alakítaná át.

Entrópiát tartalmazó megfogalmazások

Később az entrópia fogalmának bevezetésével több, általánosabb megfogalmazás is született, így például a Clausius-féle megfogalmazás felírható matematikai alakban az entrópia segítségével: $\bigtriangleup S\geqslant 0$ .

Egy még általánosabb megfogalmazás pedig rávilágít az irreverzibilis folyamatok természetére:

A természetben olyan (irreverzibilis) spontán folyamatok valósulnak meg, melyek során a termodinamikai rendszer entrópiája növekszik.

A termodinamika II. főtételét ebben a formában Clausius fogalmazta meg, és alkalmazta az entrópia fogalmát. Ezt lokális folyamatokra alkalmazta, a teljes világegyetem tekintetében nem értelmezhető (a világegyetem tágulása miatt). Viszont közbülső esetben a Földre vonatkoztatva, ha annak egyes részeinek entrópiája nő, akkor az egész entrópiája is, ezt a hipotézist nevezik "hőhalál elméletnek".

Következmények

A reverzibilis Carnot-körfolyamat termikus hatásfoka független a körfolyamatot végző anyag minőségétől:

$\eta :={\frac {W'}{Q_{1}}}=1-{\frac {Q'_{2}}{Q_{1}}}=1-{\frac {T_{2}}{T_{1}}}={\frac {T_{1}-T_{2}}{T_{1}}}$

Ha a Carnot-körfolyamatnak bármilyen kis szakasza irreverzibilis, a termikus hatásfoka a ${\frac {T_{1}-T_{2}}{T_{1}}}$ értéknél kisebb:

$\eta =1-{\frac {Q'_{2}}{Q_{1}}}={\frac {Q_{1}+Q_{2}}{Q_{1}}}\leq {\frac {T_{1}-T_{2}}{T_{1}}}$

Utóbbiból következik, hogy

${\frac {Q_{1}}{T_{1}}}+{\frac {Q_{2}}{T_{2}}}\leq 0$

vagyis a redukált hőmennyiségeknek az összege nem lehet pozitív. Ennek határesete végtelen sok hőtartályra a Clausius-féle egyenlőtlenség:

$\oint {\frac {dQ}{T}}\leq 0$

Ez alapján definiálható az entrópiafüggvény, amely (az U belsőenergia-függvényéhez hasonlóan) csak a rendszer állapotjelzőitől függ:

$S(B)-S(A)=\int _{A}^{B}{\frac {dQ_{rev}}{T}}$

Bizonyos (az integrál határaira vonatkozó) matematikai tételeket kihasználva ez átírható a következő alakba:

$\int _{A}^{B}{\frac {dQ_{irrev}}{T}}+\int _{B}^{A}{\frac {dQ_{rev}}{T}}<0$

amiből (ugyanilyen tételek okán):

$S_{B}-S_{A}=\int _{A}^{B}{\frac {dQ_{irrev}}{T}}$

azaz irreverzibilis folyamat során az entrópia a növekedése mindig nagyobb, mint a redukált hőmennyiségek integrálja.

Ha a rendszer izolált (nincs energiacsere), akkor $\delta Q=0$ miatt

$\Delta S=S_{B}-S_{A}>0$

Ez az entrópiatétel a második főtétel egyik legfontosabb alakja. Azt jelenti, hogy izolált rendszerben addig lehetségesek állapotváltozások, míg az entrópia maximális nem lesz. Ha egy izolált rendszer entrópiája maximális, a rendszer egyensúlyban van.

Látható, hogy a természetben lejátszódó folyamatok irányát szabja meg: az entrópia nem csökkenhet.

Források

• Néda Árpád, Filep Emőd: Hőtan, Erdélyi Tankönyvtanács, Kolozsvár, 2003
• Dr. Szalay Béla: Fizika ( 7. kiadás), Műszaki könyvkiadó, Budapest, 1982
• Filep Emőd, Néda Árpád: Általános fizika, Ábel kiadó, Kolozsvár, 2010
• http://www.uni-miskolc.hu/~www_fiz/KovacsE/EAtermoFULL.pdf Archiválva 2018. szeptember 20-i dátummal a Wayback Machine-ben
• Budó Ágoston: Kísérleti fizika I., Nemzeti Tankönyvkiadó Rt., 9631953130
• A hőhalál-fogalom szerepe a standard kozmológiai paradigmában