A háromszög beírt köre és hozzáírt körei
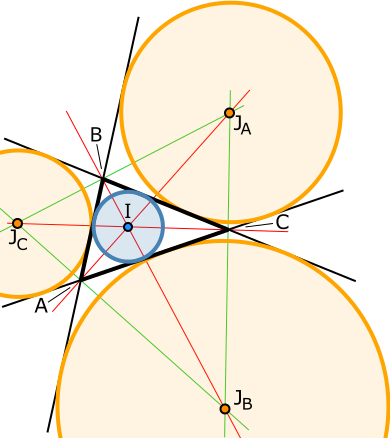
A geometriában a háromszög beírt köre vagy a háromszögbe írt kör olyan kör, amely a háromszög minden oldalát érinti, középpontja a belső szögfelezők metszéspontja, sugara a kör középpontját és az érintési pontokat összekötő szakasz (azaz a középpontból az oldalakra állított merőleges szakasz hossza). A beírt körnek nagy a jelentősége a háromszögek geometriájában.

Hozzáírt kör
[szerkesztés]A hozzáírt kör a háromszög egyik oldalát és a másik két oldalának meghosszabbítását érintő kör. Minden háromszögnek három hozzáírt köre van.
A hozzáírt körök középpontjai megkaphatók a háromszög egy belső és a háromszög két másik szögéhez tartozó külső szögfelező metszéspontjaként. Ezek a pontok olyan háromszöget alkotnak, aminek magasságpontja a beírt kör középpontja.
A beírt kör középpontja
[szerkesztés]Tétel: A háromszög beírt körének középpontja a háromszög három szögfelezőjének közös metszéspontja.
Bizonyítás: Az α szög felezőjének minden pontja egyenlő távolságra van az AB és a CA oldalaktól. Hasonlóan, a β szög felezőjének pontjai egyenlő távolságra fekszenek a BC és az AB oldalaktól. A két szögfelező metszéspontjai tehát egyenlő távolságra vannak mindhárom oldaltól, ezért a harmadik szögfelezőnek is át kell mennie ezen a ponton.
A beírt kör a háromszög minden oldalát belülről érinti, míg a hozzá írt körök kívülről érintenek egy-egy oldalt, és a két oldalegyenest a háromszögön kívül. Mindegyik kör középpontja a háromszög nevezetes pontjai közé tartozik.
A beírt kör középpontjának trilineáris koordinátái 1:1:1, baricentrikus koordinátái a:b:c, ahol a : arra utal, hogy ezek a koordináták csak konstans szorzó erejéig vannak meghatározva.
A beírt kör sugara
[szerkesztés]Jelölje a háromszög oldalait a, b, c, a háromszög kerületének felét s, a háromszög területét T!
Ekkor a beírt kör sugara
(a Hérón-képlet behelyettesítésével)
A sugár egy oldal és a rajta fekvő két szög ismeretében is kiszámítható:
A hozzáírt körök sugara
[szerkesztés]A BC oldalhoz tartozó hozzáírt kör sugara:
A másik két hozzáírt kör és sugara hasonlóan számítható.
A Hérón-képlet alapján:
- .
Hasonlóan, a másik két hozzáírt kör sugara:
- és .
Érintési pontok
[szerkesztés]A továbbiakban jelöli a C csúcs és az a oldalhoz írt kör a, illetve b oldalegyenesen levő érintési pontjainak távolságát. Hasonlóan, jelöli a B csúcs és az a oldalhoz írt kör a, illetve c oldalegyenesen levő érintési pontjainak távolságát. Analóg módon jelöljük a csúcsok és a másik két hozzáírt kör érintési pontjainak távolságát.
,
,
.
Ha az érintési pontokat összekötjük a velük szemben fekvő csúccsal, akkor a kapott egyenesek egy ponton mennek át, a Nagel-ponton.
Kapcsolódó szócikkek
[szerkesztés]Források
[szerkesztés]- Reiman István: Geometria és határterületei
- H. S. M. Coxeter und S. L. Greitzer: Zeitlose Geometrie. Klett, Berlin 1956.













