5-lemma
Megjelenés
A matematikában, azon belül a homologikus algebrában illetve az Abel-kategóriák elméletében az 5-lemma egy fontos és gyakran használt lemma. Az 5-lemma tekinthető két másik, egymással kölcsönösen duális állítás, a 4-lemmák következményének.
Állítások
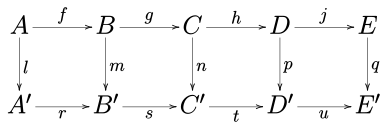
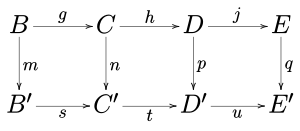
[szerkesztés]Tekintsük a következő kommutatív diagramot bármely Abel-kategóriában (például az Abel-csoportok kategóriájában) vagy a csoportok kategóriájában (utóbbi nem Abel-kategória).
Az 5-lemma szerint ha a sorok egzaktak, m és p izomorfizmusok, l epimorfizmus és q monomorfizmus, akkor n izomorfizmus.
A 4-lemmák a következőket állítják:
- kommutatív diagram sorai egzaktak, és m és p epimorfizmusok, és q monomorfizmus, akkor n epimorfizmus.
- kommutatív diagram sorai egzaktak, és m és p monomorfizmusok, és l epimorfizmus, akkor n monomorfizmus.
Jegyzetek
[szerkesztés]
Források
[szerkesztés]- WR Scott: Csoportelmélet, Prentice Hall, 1964.
- Massey, William S. (1991), A basic course in algebraic topology, vol. 127 (3rd ed.), Graduate texts in mathematics, Springer, ISBN 978-0-387-97430-9