Kötési energia
| Ehhez a szócikkhez további forrásmegjelölések, lábjegyzetek szükségesek az ellenőrizhetőség érdekében. Emiatt nem tudjuk közvetlenül ellenőrizni, hogy a szócikkben szereplő állítások helytállóak-e. Segíts a szócikk fejlesztésében további megbízható források hozzáadásával. |
A kötési energia az az energia, amely két atom közötti kötés felszakításához szükséges egy molekulában. A kötött rendszer alacsonyabb helyzeti energiával rendelkezik, mint a részei; ez tartja össze a rendszert. A szokásos megállapodás az, hogy ehhez egy pozitív kötési energia tartozik.
Általánosságban a kötési energia azt a munkát jelenti, amelyet a rendszert összetartó erővel szemben kell végezni ahhoz, hogy a test részeit olyan messze távolítsuk egymástól, amelynél a további távolítás csak elhanyagolható munkával jár.
Az elektron kötési energiája annak az energiának a mennyisége, amely ahhoz szükséges, hogy kiszabadítsuk az elektront az atombeli pályájáról.
Az atommag kötési energiája az erős kölcsönhatásból származik, és az az energia, amely ahhoz szükséges, hogy az atommagot szabad neutronokra és protonokra szedjük szét. Atomi szinten a kötési energia az elektromágneses kölcsönhatás eredménye, és azt az energiát jelenti, amely ahhoz szükséges, hogy az atomot szabad elektronokra és egy atommagra bontsuk. Az asztrofizika területén az égitestek gravitációs kötési energiája az az energia, amely ahhoz szükséges, hogy az égitestet űrhulladékká (porrá és gázzá) szedjük szét. Ez a mennyiség nem keverendő össze a gravitációs helyzeti energiával, amely ahhoz szükséges, hogy eltávolítsunk két testet – például egy égitestet és a holdját – egymástól végtelen távolságra anélkül, hogy darabjaira szednénk azokat (az utóbbi energia alacsonyabb).
Definíció
[szerkesztés]Az kötési energia definíciója az IUPAC megfogalmazásában: bizonyos vegyértékű atomok között az adott típusú kötés felszakításához szükséges energia.[1]
Tömegdefektus
[szerkesztés]A tömegdefektus az atommagok tömege és a különálló alkotórészek tömegének összege közötti különbség jelensége, amelyet Albert Einstein fedezett fel 1905-ben. Azzal magyarázható, hogy az atomok létrejöttekor energia szabadul fel, amely adott mennyiségű tömegcsökkenéssel jár együtt. A tömegdefektus az energia és a tömeg ekvivalenciáját leíró E = mc2 képlettel magyarázható.
A kötött rendszer alacsonyabb energiájú, mint az alkotórészei, amikor nincsenek kötött állapotban, emiatt a tömegüknek kisebbnek kell lennie, mint az összetevők tömegeinek összege. Olyan rendszerek esetén, melyeknél a kötési energia alacsony, ez a kötés utáni „veszteség” elég kicsi hányada lehet a teljes tömegnek. A nagy kötési energiájú rendszerek esetén azonban a hiányzó tömeg könnyen mérhető rész.
Mivel a rendszerben minden energiaforma (amelyek nincs nettó impulzusa) rendelkezik tömeggel, érdekes kérdés, hogy hová lesz a kötési energia. A válasz nem az, hogy „átalakul” energiává (ez egy gyakori félreértés); hanem az, hogy átalakul hővé vagy fénnyé, és ebben a formában eltávozhat más helyre. A kötési energiából származó „tömegdefektus” csupán egy olyan tömeg, amely eltávozott. Mégis a tömeg megmarad, mivel a tömeg megmaradó mennyiség minden egyes megfigyelő rendszeréből nézve, amíg a rendszer zárt (hiszen az energia megmaradó mennyiség, a tömeg pedig ekvivalens az energiával). Emiatt, ha a kötési energia fény energiájává alakul, a tömeg például foton tömegévé alakul.
Például, ha két nagy test (például a Föld és egy meteoroid) a gravitációs mező vonzó hatása miatt összeütközik, a becsapódáskor keletkező hő a testek mozgási energiájából, áttételesen pedig a gravitációs mező energiájából származik. A rendszer azonban nem veszt tömeget (a kötési energiával kapcsolatosan) egészen addig, amíg ez a hő ki nem sugárzódik a világűrbe (ekkor azonban nyílt rendszernek kell tekintenünk a Földet és a meteort).
Egészen hasonló megfontolások érvényesek a kémiai és atommagbeli helyzetre. A magreakciókban viszont az a tömeghányad, amely eltávozik fény vagy hő formájában, és mint kötési energia jelenik meg, gyakran sokkal nagyobb hányada a rendszer tömegének. Ez amiatt van, mert az erős kölcsönhatás (a magerő) sokkal erősebb a többi erőnél.
Magreakciók esetén a „fény” – amelynek ki kell sugárzódnia, hogy eltávozzon a kötési energia – közvetlenül gamma-sugárzás lehet. De itt ismét nem jelenik meg tömegveszteség az elméletben, amíg a sugárzás el nem távozik, és amíg még a rendszer részének tekintjük, hiszen addig a tömeg még jelen van gamma-foton(ok) tömegeként.
A magfúzió és a maghasadás által kibocsátott energia megegyezik a fűtőanyag és a keletkező fúziós vagy hasadási termékek kötési energiájának különbségével. A gyakorlatban ezt az energiát a fűtőanyag és a termékek tömegének különbségéből is kiszámítható, amikor a hő és a sugárzás eltávozott.
Atomok kötési energiája
[szerkesztés]Egyetlen atom kötési energiája (E_b: binding energy) a következőképp számolható:
ahol:
- c a fénysebesség
- ms a különálló (separated) nukleonok tömege
- mb a kötött (bound) mag tömege
- Z a kötött mag rendszáma
- mp egy proton tömege
- N a neutronok száma
- mn egy neutron tömege
Pontosabb számítások esetén figyelembe kell venni, hogy táblázatokban többnyire a semleges atomok vannak, azaz az elektronokat is figyelembe kell venni a számításoknál.
Egy konkrét mennyiségi példa: a deuteron
[szerkesztés]A deuteron a deutériumatom magja. Egy protont és egy neutront tartalmaz. Az összetevők tömegei:
- mproton = 1,007825 u (u az atomi tömegegység)
- mneutron= 1,008665 u
- mproton + mneutron = 1,007825 u + 1,008665 u = 2,01649 u
A deuteron tömege:
- 2H atommagjának tömege = 2,014102 u
A tömegkülönbség = 2,01649 u – 2,014102 u = 0,002388 u. Mivel a nyugalmi tömeg és az energia közötti váltószám 931,494 MeV/u, így a deuteron kötési energiája
- 0,002388 · 931,494 MeV/u = 2,224 MeV
Másképpen kifejezve, a kötési energia [0,002388/2,01649] · 100% = nagyjából 0,1184%-a a teljes tömeghez tartozó energiának. Ennek 1,07·1014 J/kg = 107 TJ/kg energiatartalom felel meg.
Ide tartozó mennyiség még a fajlagos kötési energia, ami nem más, mint az egy nukleonra jutó kötési energia. Jele: ε.
ε = ΔE / A
A mag kötési energiájának görbéje
[szerkesztés]Az elemek periódusos rendszerében a könnyű elemek a hidrogéntől a nátriumig tartó sorozata mérhetően egyre nagyobb kötési energiával rendelkeznek nukleononként, ahogy a tömegszám növekszik. Ez a növekedés az egy nukleonra eső erő növekedése miatt van, mivel minden újabb nukleont vonz az összes többi nukleon, és egy sokkal szorosabban kötődnek az egészhez.
A növekvő kötési energia tartományát egy relatív stabilitás tartománya követi (szaturáció) a magnéziumtól a xenonig tartó sorozatban. Ebben a tartományban a mag elég naggyá válik, hogy a magerők ne tudják átérni a magot. Ebben a tartományban a magerők növekedő vonzó hatását nagyjából ellensúlyozza a protonok közötti elektromágneses erők taszításának növekedése növekvő tömegszámnál.
Végül a xenonnál nehezebb elemekben a nukleononkénti kötési energia csökken, ahogy az tömegszám növekszik. Ebben a tartományban az elektromágnesség taszító hatásának növekedése nagyobb, mint a magerők vonzó hatásának növekedése.
A kötési energia görbéjének csúcsánál a nikkel-62 található, a legszorosabban kötött mag, ezt pedig a vas-58 és a vas-56 követi. (Ez az alapvető oka, hogy a vas és a nikkel olyan gyakori anyag a bolygók belsejében, mivel ezek bőségesen termelődnek szupernóvákban.
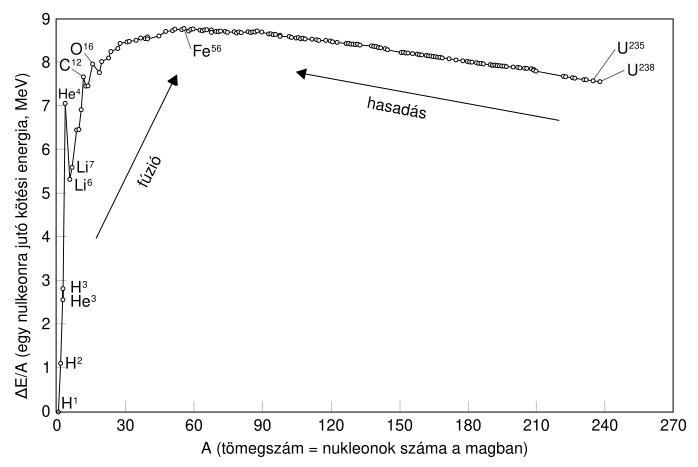
A kötésienergia-görbe közepes méretű magoknál található maximuma a kétféle ellentétes erő hatótávolságának a különbsége miatt jön létre. A vonzó magerő (erős kölcsönhatás), amely a protonokat és a neutronokat egymástól egyforma távolságban tartja, kis hatótávolságú, erős exponenciális csökkenés tapasztalható az erő nagyságában a távolság növekedésével. Ellenben a taszító elektromágneses kölcsönhatás – amely a protonokat eltávolítaná egymástól – jóval kevésbé csökken a távolsággal (a távolság négyzetével fordított arányban). Azoknál a magoknál, amelyek négy nukleonátmérőnél nagyobb átmérőjűek, a taszító hatás – amelyet a beépülő protonok okoznak – jobban csökkenti a kötési energiát, mint a hozzáadott újabb nukleonokra ható vonzó magerők vonzó hatására bekövetkező kötésienergia-növekedés; emiatt a mag egyre lazábban kötött lesz, ahogy a mérete növekszik, bár a legtöbbjük még stabil. Végül a 209-nél több nukleont tartalmazó magok (6 nukleonnyi átmérőnél nagyobbak) túl nagyok lesznek ahhoz, hogy stabilak legyenek, és spontán módon bomlanak könnyebb magokra.
A fúzió során a nagyon könnyű elemek kapcsolódnak össze szorosabban kötött elemekké (például a hidrogén héliummá), a maghasadáskor (fisszió) pedig a energia szabadul fel, miközben a legnehezebb elemek (például urán és plutónium) lazábban kötött elemekre (például báriumra és kriptonra) hasadnak. Mindkettő kölcsönhatás energiát termel, mivel erősebben kötött közepes méretű elemeket hoz létre.
A kötési energia mérése
[szerkesztés]Ahogy feljebb a deutérium példáján látható, a mag kötési energiája elég nagy ahhoz, hogy könnyedén mérhető legyen mint tömegdeficit a tömeg–energia ekvivalencia alapján. Az atom kötési energiája egyszerűen az a kibocsátott energia, amely a szabad nukleonok atommaggá egyesítésekor felszabadul. Minden mag, amely elég sokáig létezik, hogy megmérjék a tömegét, mérhetően könnyebb, mint a megfelelő számú szabad proton és neutron együttese. Ha ezt a tömegkülönbség – amelyet tömegdefektusnak hívnak – ismert, akkor Einstein E=mc² képletével könnyedén kiszámítható bármely mag kötési energiája.
Például az atomi tömegegység (1,000000 u) definíció szerint a 12C atom tömegének 1/12-ed része – de a 1H atom (amely egy proton és egy elektron) atomtömege 1,007825 u, tehát minden egyes 12C mag átlagosan a tömegének nagyjából 0,8%-át elvesztette a kialakulása során, ebből a tömegkülönbségből számítható a kötési energiája.
Jegyzetek
[szerkesztés]- ↑ IUPAC Gold Book - bond energy. goldbook.iupac.org, 2020

