Lekötött gráf

Lekötött gráf, ami egy maximális síkgráf (sárga) és két merev körű gráf (piros és kék) klikk-összeg művelettel való összeragasztásával lett előállítva. A piros merev körű gráf tovább bontható négy maximális síkgráf (két él és két háromszög) klikkösszegére.

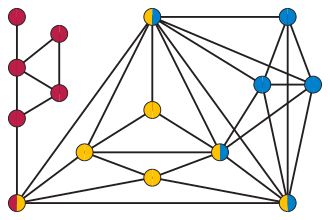
A matematika, azon belül a gráfelmélet területén egy lekötött gráf vagy strangulált gráf (strangulated graph) a merev körű gráfok fogalmának általánosítása: olyan összefüggő gráf, melynek bármely, három élnél hosszabb feszített körét kitörölve a maradék gráf szétesne. Más megfogalmazásban, azok az összefüggő gráfok, melyek minden periferikus köre háromszög ($K_{3}$).

Példák

Egy maximális síkgráf, vagy általánosabban bármely poliédergráf periferikus körei pontosan megegyeznek a gráf síkba ágyazásának tartományaival. Ezért egy poliédergráf pontosan akkor lekötött, ha minden tartománya háromszög, vagy ami ezzel ekvivalens, ha maximális síkbarajzolható gráf. Minden merev körű gráf lekötött gráf, mivel a merev körű gráfok minden feszített köre háromszög, így nincsenek hosszabb körök, melyeket törölni lehetne.

Jellemzés

Két gráf klikkösszegét úgy képezzük, hogy két azonos méretű klikkel rendelkező gráfot azonosítunk, majd esetleg kitöröljük a klikk néhány élét. A klikkösszeg a lekötött gráfoknál releváns változatában az éltörlési lépésre nem kerül sor. Két lekötött gráf közötti az ilyen klikkösszeg-művelet egy újabb lekötött gráfot eredményez, hiszen az összeg bármely hosszú feszített körének vagy az egyik, vagy a másik oldalra kellene szorítkoznia (hiszen egyébként az összeg két oldala közötti körben a két oldal közötti átlépés helyén húr húzódna), és annak az oldalnak a kör kitörlésével formált, nem összefüggő részeinek a klikkösszeg művelettől függetlenül is különállónak kell maradniuk. Minden merev körű gráf ilyen módon felbontható teljes gráfok klikkösszegére, továbbá minden maximális síkgráf felbontható 4-szeresen csúcsösszefüggő maximális síkgráfok klikkösszegére.

Ahogy (Seymour & Weaver 1984) kimutatja, ezek a lekötött gráfok egyedül lehetséges építőelemei: a lekötött gráfok pontosan azok a gráfok, melyek teljes gráfokból, illetve maximális síkbarajzolható gráfokból a klikkösszeg művelet segítségével előállíthatók.

Kapcsolódó szócikkek

• Élperfekt gráf, olyan gráf, melynek minden páratlan köre háromszög

Fordítás

• Ez a szócikk részben vagy egészben a en című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

• Seymour, P. D. & Weaver, R. W. (1984), "A generalization of chordal graphs", Journal of Graph Theory 8 (2): 241–251, DOI 10.1002/jgt.3190080206.