Létragráf
| Létragráf | |
 | |
| Az L8 létragráf | |
| Csúcsok száma | 2n |
| Élek száma | 3n−2 |
| Derékbőség | 4, ha n>1 |
| Kromatikus szám | 2 |
| Élkromatikus szám | 3, ha n>2 2, ha n=2 1, ha n=1 |
| Egyéb | Egységtávolsággráf Hamilton-körű Síkbarajzolható Páros |
| Jelölés | Ln |
A matematika, azon belül a gráfelmélet területén az Ln-nel jelölt létragráf (ladder graph) egy 2n csúccsal és 3n−2 éllel rendelkező összefüggő, irányítatlan, síkbarajzolható gráf.[1]
A létragráf előállítható két útgráf Descartes-szorzataként, amennyiben az egyik útgráf csak egyetlen éllel rendelkezik: Ln,1 = Pn × P2.[2][3]
Tulajdonságok
[szerkesztés]A konstrukciós szabály alapján nyilvánvaló, hogy az Ln létragráf a G2,n rácsgráffal izomorf, és valóban emlékeztet egy n fokkal rendelkező létrára. Rendelkezik Hamilton-körrel, girthparamétere 4 (ha n>1), élkromatikus száma pedig 3 (ha n>2). A gráf négy sarki helyzetű csúcsának fokszáma 2, a többi csúcsé 3. Az Ln létragráf teljes párosításainak száma megegyezik az Fn+1 Fibonacci-számmal.
A létragráf kromatikus száma 2, kromatikus polinomja pedig .
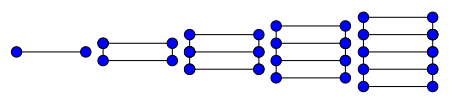
-
A létragráf kromatikus száma 2.
Létrafok-gráf
[szerkesztés]Néha létragráf alatt az n × P2 létrafok-gráfot (ladder rung graph) értik, azaz n db 2 hosszúságú útgráf diszjunkt unióját.

Körkörös létragráf
[szerkesztés]A létragráf négy 2 fokszámú csúcsát egyenesen összekötve, avagy egy n≥3 hosszúságú kör és egy él Descartes-szorzatával a körkörös létragráf (circular ladder graph), CLn áll elő.[4]
Szimbolikusan: CLn = Cn × P1.
A körkörös létragráf 2n csúccsal és 3n éllel rendelkező, összefüggő síkbarajzolható gráf Hamilton-körrel, de kizárólag akkor páros, ha n páros.
A körkörös létragráfok a hasábok poliédergráfjai, ezért hasábgráfnak is nevezik őket.
Körkörös létragráfok:
 CL3 |
 CL4 |
 CL5 |
 CL6 |
 CL7 |
 CL8 |
Möbius-létragráf
[szerkesztés]Egy létragráf négy 2 fokszámú csúcsát keresztben összekötve 3-reguláris gráf jön létre, amit Möbius-létrának neveznek.

Fordítás
[szerkesztés]- Ez a szócikk részben vagy egészben a Ladder graph című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
- Ez a szócikk részben vagy egészben a Leitergraph című német Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek
[szerkesztés]- ↑ Weisstein, Eric W.: Ladder Graph (angol nyelven). Wolfram MathWorld
- ↑ Hosoya, H. and Harary, F. "On the Matching Properties of Three Fence Graphs." J. Math. Chem. 12, 211-218, 1993.
- ↑ Noy, M. and Ribó, A. "Recursively Constructible Families of Graphs." Adv. Appl. Math. 32, 350-363, 2004.
- ↑ (2013. szeptember 1.) „Total Embedding Distributions of Circular Ladders”. Journal of Graph Theory 74 (1), 32–57. o. DOI:10.1002/jgt.21690.


