Egész számok

Ez a szócikk a matematikai értelemben vett egész számokról szól. Hasonló címmel lásd még: Egész (informatika).

Egész számoknak nevezzük a 0,1,2, … és −1,−2, … számokat. Az egész számok halmazának tehát részhalmaza a természetes számok halmaza.

Az egész számok halmazát Z-vel (általában tipográfiailag kiemelve, mint Z vagy $\mathbb {Z}$ ) jelöljük. Az utóbbi Unicode-ja U+2124. A jelölés a német Zahlen (számok) szó rövidítése.^[1] Az egész számok halmaza végtelen, hisz a természetes számok halmazát (és minden természetes szám ellentettjét) tartalmazza. Sokkal meglepőbb, hogy az egész számok halmazának számossága megegyezik a természetes számok halmazának számosságával. Szemléletesen ez azt jelenti, hogy matematikai értelemben ugyanannyi elemük van, holott az egyik halmaz tartalmazza a másikat.

Az egész számok természetes rendezése növekvő sorrendben: …, −3, −2, −1, 0, 1, 2, 3, … A számelmélet az egész számokat vizsgálja.

Számítógépben az egész számokat rendszerint az int, integer, long, long long, BigInteger és más, hasonló nevű számtípusok ábrázolják.

Matematikai definíció

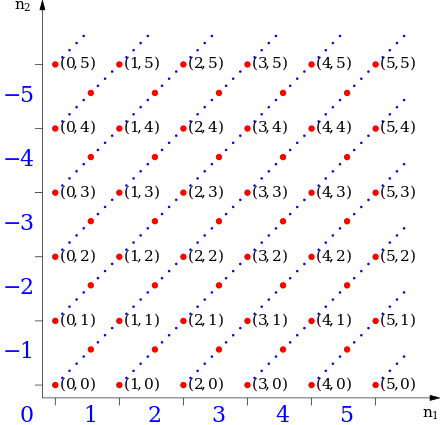
Az egész számokat az általános iskolában intuitívan vezetik be a kivonás segítségével; illetve úgy, hogy a természetes számokhoz hozzáveszik azok ellentettjeit. Azonban ez a definíció megnehezíti a különböző műveletek működésének ellenőrzését (jóldefiniáltság, megkívánt tulajdonságok), mivel esetszétválasztást igényel.^[2] Ezért a halmazelmélet absztraktabb konstrukciót használ.^[3]

A természetes számok $\mathbb {N}$ halmazát ismertnek feltételezve a következőképpen definiálhatjuk az egész számokat: Tekintsük a $\mathbb {N} \times \mathbb {N}$ Descartes-szorzatot, amely természetes számok rendezett párjaiból áll. Értelmezzük ezeken a párokon a (m,n)~(m',n'), ha m+n'=m'+n relációt, az (m,n)+(m',n')=(m+m',n+n') összeadást, és az $(m,n)\cdot (m'n')=(m\cdot m'+n\cdot n',m\cdot n'+m'\cdot n)$ szorzást, valamint az (m,n)≤(m'n')-t, ha m+n'≤m'+n relációt. A ~ reláció ekvivalenciareláció. Az ekvivalenciaosztályok halmazát jelöljük $\mathbb {Z}$ -vel. Az így nyert $\mathbb {Z}$ halmazt nevezzük az egész számok halmazának.^[4]

Mindegyik ekvivalenciaosztály reprezentálható az (n,0) vagy (0,n) (vagy akár egyszerre mindkettő) alakú elemével. Az n természetes számot az [(n,0)] osztály azonosítja (más szóval a természetes számok beágyazhatók $\mathbb {Z}$ -be), illetve a [(0,n)] osztályt –n-nel jelöljük (így megkaptuk az összes ekvivalenciaosztályt, a [(0,0)] osztályt kétszer, hiszen –0=0).

Így az [(a,b)]-t

{\begin{cases}a-b,&{\mbox{ha }}a\geq b\\-(b-a),&{\mbox{ha }}a<b\end{cases}}

módon jelölhetjük.

Ez a jelölés az egész számok megszokott reprezentációját adja: {... –3, –2, –1, 0, 1, 2, 3, ...}.

Például:

{\begin{aligned}0&=[(0,0)]&=[(1,1)]&=\cdots &&=[(k,k)]\\1&=[(1,0)]&=[(2,1)]&=\cdots &&=[(k+1,k)]\\-1&=[(0,1)]&=[(1,2)]&=\cdots &&=[(k,k+1)]\\2&=[(2,0)]&=[(3,1)]&=\cdots &&=[(k+2,k)]\\-2&=[(0,2)]&=[(1,3)]&=\cdots &&=[(k,k+2)].\end{aligned}}

$\mathbb {Z}$ elemei a szokásos műveletekkel gyűrűt alkotnak. Az (a,b) pár additív inverze a (b,a) pár.

A konstrukció hasonlóan működik, ha a természetes számok halmazába nem veszik bele a nullát. Ekkor választhatók a következő reprezentáns elemek: az $n$ természetes szám reprezentánsa $(n+1,1)$ , az $n$ negatív egészé $(1,1+n)$ , és a nulláé $(1,1)$ .

Tulajdonságok

Az egész számok halmaza zárt (a négy alapművelet közül) az összeadásra, a kivonásra és a szorzásra. Az összeadás neutrális eleme a 0. Az additív inverz az ellentett, egy $n$ egész szám ellentettje $-n$ . A szorzás egységeleme az 1.

Az egész számok halmaza (a szokásos rendezéssel) lineárisan rendezett. A rendezés segítségével definiálhatók a következő függvények:

a szignumfüggvény:

\operatorname {sgn}(x):={\begin{cases}-1&{\text{ha }}\quad x<0\\~~\,0&{\text{ha }}\quad x=0\\~~\,1&{\text{ha }}\quad x>0\end{cases}}

és az abszolútértékfüggvény:

|x|=\operatorname {abs} (x):={\begin{cases}~~\,x&{\text{ha }}\quad x\geq 0\\-x&{\text{ha }}\quad x<0\end{cases}}

A kettő közötti összefüggés:

x=\operatorname {sgn}(x)\,|x|

Az egész számok halmaza az összeadással Abel-csoportot (kommutatív csoportot), a szorzással kommutatív félcsoportot képez. A disztributivitás miatt az egész számok halmaza a fent definiált összeadással és szorzással gyűrűt alkot.

Az egész számok euklideszi gyűrűt alkotnak a szokásos maradékos osztással és az abszolútértékkel, mint normával. Emiatt két egész szám legnagyobb közös osztója euklideszi algoritmussal számítható. Az euklideszi gyűrű tulajdonságból következik az egyértelmű törzstényezős felbontás is.

Számossága

Az egész számok halmazának számossága megszámlálhatóan végtelen (szokásos jelöléssel $\aleph _{0}$ ), ami megegyezik a természetes számok számosságával. Két halmaz számossága ugyanis akkor egyezik meg, ha létezik egy, a két halmaz között értelmezett bijekció. Ebben az esetben is létezik ilyen függvény, mégpedig pl:

$f:\mathbb {Z} \rightarrow \mathbb {N}$

$f(x):={\begin{cases}2x&{\mbox{ha }}x\geq 0\\-2x-1&{\mbox{ha }}x<0\end{cases}}$

Vagyis minden nemnegatív egész számhoz hozzárendeljük a páros természetes számokat, minden negatív számhoz pedig a páratlanokat. Az egész számok minden elemét képezzük valahova, és az összes természetes számba képezünk, ezért ez bijekció, azaz a két halmaz számossága megegyezik.

Hasonló konstrukciók

Általánosabban, kommutatív félcsoportokkal megismételhető a konstrukció. Az így létrejött csoport a Grothendieck-csoport. Így az egész számok a természetes számok Grothendieck-csoportja.
A Gauss-egészek és az Eisenstein-egészek az egész számok két különböző bővítése komplex számokká.
Az egész számok ${\widehat {\mathbb {Z} }}$ provéges teljessé tétele $\mathbb {Z}$ összes véges faktorcsoportjának projektív limesze (inverz limesze), az inverz rendszert az osztókhoz rendelt faktorcsoportok közti természetes epimorfizmusok adják. Így jönnek létre a provéges egészek, melyeket a ${\widehat {\mathbb {Z} }}$ szimbólum jelöl.

Fordítás

Ez a szócikk részben vagy egészben a Ganze Zahl című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Jegyzetek

↑ Jeff Miller: Earliest Uses of Symbols of Number Theory, 2010-08-29. [2010. január 31-i dátummal az eredetiből archiválva]. (Hozzáférés: 2019. május 27.)
↑ Mendelson, Elliott (2008), Number Systems and the Foundations of Analysis, Dover Books on Mathematics, Courier Dover Publications, p. 86, ISBN 978-0-486-45792-5, <https://books.google.com/books?id=3domViIV7HMC&pg=PA86>.
↑ Ivorra Castillo: Álgebra
↑ Campbell, Howard E.. The structure of arithmetic. Appleton-Century-Crofts, 83. o. (1970). ISBN 978-0-390-16895-5

További információk

Források

Az egész számok a MathWorld-ön

Matematikaportál • összefoglaló, színes tartalomajánló lap

[1] Jeff Miller: Earliest Uses of Symbols of Number Theory, 2010-08-29. [2010. január 31-i dátummal az eredetiből archiválva]. (Hozzáférés: 2019. május 27.)

[2] Mendelson, Elliott (2008), Number Systems and the Foundations of Analysis, Dover Books on Mathematics, Courier Dover Publications, p. 86, ISBN 978-0-486-45792-5, <https://books.google.com/books?id=3domViIV7HMC&pg=PA86>.

[3] Ivorra Castillo: Álgebra

[Campbell-1970-p83-4] Campbell, Howard E.. The structure of arithmetic. Appleton-Century-Crofts, 83. o. (1970). ISBN 978-0-390-16895-5

[1]

[2]

[3]

[4]